33.Квантование сигнала

Так как математической моделью непрерывного сигнала является случайный процесс , мгновенное значение сигнала представляет собой случайную величину. Диапазон её изменения, называемый непрерывной шкалой мгновенных значений сигнала ограничен значениями и , что отражает условие физической реализуемости сигнала. Непрерывную шкалу мгновенных значений

сигнала разбивают на интервалов, которые называют шагами квантования. Границами шагов квантования являются значения . Из множества мгновенных значений, которые принадлежат му шагу квантования , только одно значение является разрешенным (й уровень квантования). Любое другое из указанного множества значений округляется до . Совокупность величин образует дискретную шкалу уровней квантования. Если эта шкала равномерная, т.е. разности значений

постоянна на всём протяжении непрерывной шкалы мгновенных значений сигнала , квантование называют равномерным. Если постоянство значений не выдерживается – квантование неравномерное. Благодаря простоте технической реализации равномерное квантование получило наиболее широкое распространение.

В результате замены мгновенного значений сигнала соответствующим уровнем квантования возникает погрешность

,

которую называют ошибкой квантования. Эта погрешность является случайной величиной. Но чаще всего интересует её максимальное значение

и среднеквадратическое отклонение от всего диапазона изменения мгновенных значений сигнала. Используются также приведенные значения этих величин

,

.

С позиций минимизации наибольшей возможной ошибки квантования непрерывную шкалу мгновенных значений сигнала целесообразно разбить на одинаковых шагов квантования

и уровни квантования разместить в середине каждого шага. при этом максимальная ошибка квантования не превышает . Если каждый уровень квантования выбран равным нижней (верхней) границе шага квантования, максимальная ошибка квантования возрастает до величины .

Рис.

Среднеквадратическое отклонение ошибки квантования для го шага зависит не только от шага и расположения в нём уровня квантования, но и от закона распределения мгновенных значений сигнала в пределах этого шага

,

где функция плотности вероятности мгновенных значений сигнала .

Считая шаги квантования малыми по сравнению с диапазоном изменения сигнала, плотности в пределах каждого го шага можно принять постоянной и равной некоторому среднему значению, например . При таких предположениях минимальная среднеквадратическая ошибка достигается при расположении уровня квантования в середине шага

.

Преобразовав подкоренное выражение к виду

,

отметим, что дисперсия ошибки квантования на м шаге равна равномерно распределенного на этом шаге сигнала, умноженной на вероятность попадания мгновенного значений сигнала в пределы данного шага. Дисперсия полной ошибки квантования для всей непрерывной шкалы мгновенных значений сигнала определяется как математическое ожидание дисперсий на отдельных шагах квантования:

.

При одинаковых шагах квантования

.

Так как принимаем

,

то

.

Таким образом, при квантовании с постоянным шагом и размещением уровней квантования в середине шага (равномерное квантование) среднеквадратическая ошибка квантования как для равномерного, так и произвольного распределения мгновенных значений сигнала одинакова:

.

Шум квантования. При квантовании сигнала по уровню случайный процесс заменяется ступенчатой зависимостью . Ошибку квантования , которая изменяется во времени и также представляет собой случайный процесс, называют шумом квантования:

.

Сохраняя ранее введенные предположения (о малости шага квантования и равномерности распределения в нём мгновенных значений сигнала) и считая случайные процессы и эргодическими, среднеквадратическую ошибку равномерного квантования можно определить по реализации (рис. ). В пределах каждого квантования зависимость заменяется прямой , где переменный угол наклона прямой. При размещении уровней квантования в середине каждого шага математическое ожидание ошибки равно нулю, а её среднеквадратическое значение определяется выражением

.

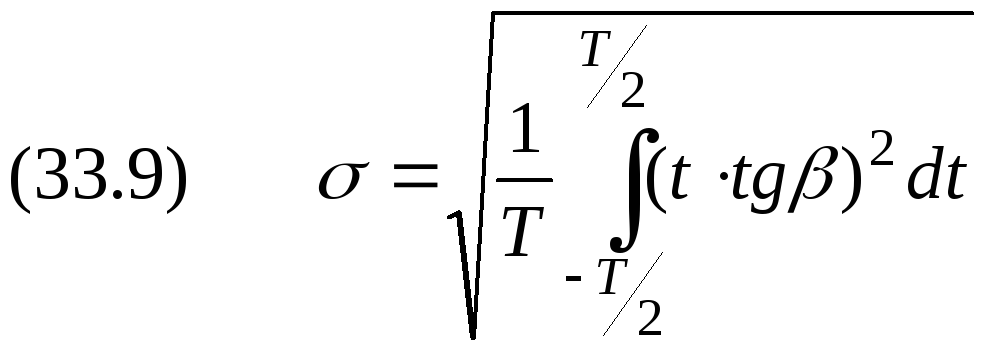Так как , то , что соответствует ранее полученному значению (см. выражение (33.7)).

При заданной допустимой среднеквадратической ошибке квантовании и отсутствии помех число уровней квантования находим из соотношения

.

Однако при неравномерном законе распределение мгновенных значений сигнала квантование с постоянным шагом не является оптимальным по критерию минимума среднеквадратической ошибки . Квантуя участки с менее вероятными значениями сигнала с большим шагом, указанное значение среднеквадратической ошибки можно уменьшить.