
- •Н.Н. Куцый теория информации
- •1. О понятии "информация"
- •2. Этапы обращения информации
- •3. Информационные системы
- •4. Система передачи информации: основные понятия и определения
- •5. Уровни проблем передачи информации
- •6. Теория информации
- •7. Понятия сигнала и его модели
- •8. Формы представления детерминированных сигналов
- •9. Ортогональные представления сигналов
- •10. Временная форма представления сигнала
- •11. Частотная форма представления сигнала. Спектры периодических сигналов
- •12. Распределение энергии в спектре периодического сигнала
- •13. Частотная форма представления сигнала. Спектры непериодических сигналов
- •14. Распределение энергии в спектре непериодического сигнала
- •15.Соотношения между длительностью импульсов и шириной их спектра
- •16.Спектральная плотность мощности детерминированного сигнала
- •17.Функция автокорреляции детерминированного сигнала
- •18.Случайный процесс как модель сигнала
- •19.Стационарные и эргодические процессы
- •20.Спектральное представление случайных сигналов
- •21.Частотное представление стационарных случайных процессов (дискретный спектр)
- •22.Частотное представление стационарных случайных сигналов. Непрерывные спектры
- •23.Основные свойства спектральной плотности
- •24.Преимущества цифровой формы представления сигналов
- •25.Общая постановка задачи дискретизации
- •26.Способы восстановления непрерывного сигнала
- •27.Критерии качества восстановления
- •28.Методы дискретизации посредством выборок
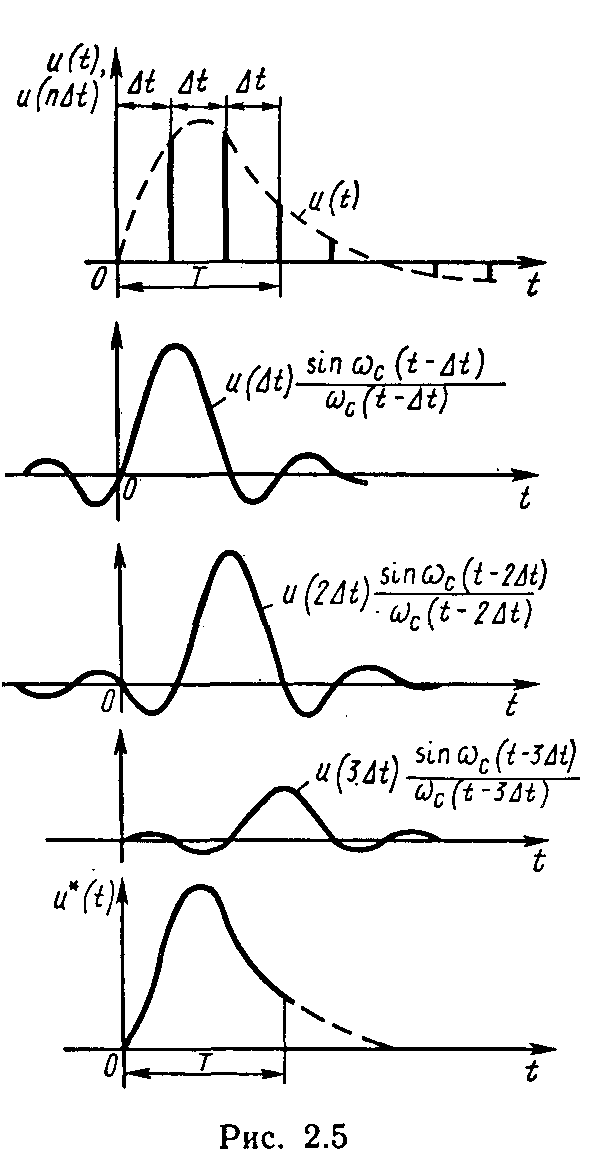
- •29.Равномерная дискретизация. Теорема котельникова
- •30.Теоретические и практические аспекты использования теоремы котельникова
- •31.Дискретизация по критерию наибольшего отклонения
- •32.Адаптивная дискретизация
- •33.Квантование сигнала
- •34.Квантование сигналов при наличии помех
- •35.Геометрическая форма представления сигналов
- •36.Энтропия как мера неопределенности выбора
- •37.Свойства энтропии
- •38.Условная энтропия и её свойства
- •39.Энтропия непрерывного источника информации (дифференциальная энтропия)
- •40.Свойства дифференциальной энтропии
- •41.Количество информации как мера снятой неопределенности
- •42.Эпсилон-энтропия случайной величины
- •43.Информационные характеристики источника сообщений и канала связи. Основные понятия и определения
- •44.Информационные характеристики источника дискретных сообщений
- •45.Информационные характеристики дискретных каналов связи
- •46.Информационные характеристики источника непрерывных сообщений
- •47.Информационные характеристики непрерывных каналов связи
31.Дискретизация по критерию наибольшего отклонения
В
процессе дискретизации непрерывная
функция
![]() ,
которая имеет
,
которая имеет
![]() ограниченных производных, аппроксимируется
многочленом
ограниченных производных, аппроксимируется
многочленом
![]() й
степени. В зависимости от выбранного
способа восстановления он может быть
аппроксимирующим или экстраполирующим.
Задача обеспечения минимальной
погрешности при восстановлении сигнала
на практике не ставится. Обычно указывается
её допустимое значение
й
степени. В зависимости от выбранного
способа восстановления он может быть
аппроксимирующим или экстраполирующим.
Задача обеспечения минимальной
погрешности при восстановлении сигнала
на практике не ставится. Обычно указывается
её допустимое значение
![]() .
.
Погрешность
восстановления
![]() функции
функции
![]() многочленом
многочленом
![]() на каждом участке аппроксимации
определяется остаточным членом
на каждом участке аппроксимации
определяется остаточным членом
![]()
![]() .
.
Следовательно,
шаг дискретизации должен быть выбран
из условия
![]() .
.


Выбор
аппроксимирующего многочлена более
высокой степени при малой допустимой
погрешности
![]() обеспечивает меньшее число отсчётов,
однако при этом существенно возрастает
сложность технической реализации
метода. Поэтому обычно ограничиваются
многочленами нулевой, первой и второй
степеней.
обеспечивает меньшее число отсчётов,
однако при этом существенно возрастает
сложность технической реализации
метода. Поэтому обычно ограничиваются
многочленами нулевой, первой и второй
степеней.
В качестве интерполирующего многочлена чаще других используются многочлены Лагранжа, в качестве экстраполирующих – многочлены Тейлора.
Дискретизация с использованием интерполирующих многочленов Лагранжа. Интерполирующий многочлен Лагранжа при равномерной дискретизации может быть записан в виде
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() .
.
Значение
остаточного члена
![]()
![]() ,
,
где
![]() максимальный
во всём интервале преобразования модуль
максимальный
во всём интервале преобразования модуль
![]() производной
сигнала
производной
сигнала
![]() .
.
Дискретизация с использованием экстраполирующих многочленов Тейлора. Экстраполирующий многочлен Тейлора определяется выражением
![]() ,
,
где
![]() я
производная сигнала
я
производная сигнала
![]() в момент времени
в момент времени
![]() .
.
Оценка снизу для остаточного члена имеет вид
![]() ,
,
![]() .
.
32.Адаптивная дискретизация
Если ранее рассмотренные методы и алгоритмы дискретизации были рассчитаны на все множества возможных реализаций сигнала и потому опирались на предельные значений его динамических характеристик, то при адаптивной дискретизации мы ориентируемся на динамические характеристики конкретной реализации, что позволяет получить минимальное число выборок, обеспечивающих восстановление этой реализации с заданной точностью.
В
основе принципа адаптивной дискретизации
лежит непосредственное слежение за
текущей погрешностью восстановления
сигнала
![]() .
.
Наиболее
широкое применение на практике получили
алгоритмы дискретизации с адаптацией
по длине интервала аппроксимации. В
процессе последовательного наращивания
интервала аппроксимации производится
сравнение сигнала
![]() с воспроизводящей функцией
с воспроизводящей функцией
![]() ,
формируемой с учётом текущих значений
динамических характеристик сигнала.
Когда погрешность воспроизведения
достигает заданного значения
,
формируемой с учётом текущих значений
динамических характеристик сигнала.
Когда погрешность воспроизведения
достигает заданного значения
![]() ,
наращивание интервала прекращается и
производится отсчёт. Интервалы времени
между отсчётами при этом оказываются
произвольными.
,
наращивание интервала прекращается и
производится отсчёт. Интервалы времени
между отсчётами при этом оказываются
произвольными.
В качестве воспроизводящих функций наиболее часто используются степенные алгебраические полиномы нулевой и первой степеней
![]()
или
![]() ,
,
где
![]() действительные
коэффициенты.
действительные
коэффициенты.
При этом возможны как интерполяционные, так и экстраполяционные способы адаптивной дискретизации. Интерполяционные способы не нашли широкого применения, поскольку их реализация связана с запоминанием сигнала на интервале аппроксимации м выполнением большого числа вычислительных операций.
