f

Таблица 5.2.

Формы обращений к функциям

Входное выражение	Название формы	Значение
Sin[Pi/2]	standard	1
Sin@(Pi/2)	prefix	1
Pi/2//Sin	postfix	1
N@Sqrt@2	prefix	1.41421

@x - префиксная форма (prefix form),

x//f - постфиксная форма (postfix form).

Примеры обращений даны в таблице 5.2.

Отметим, что префиксная форма имеет наиболее высокий приоритет, а постфиксная – самый низкий, так что Sin@x+y = y+Sin[x], а x+y//Sin = Sin[x+y].

Для функций нескольких переменных кроме стандартной существует также инфиксная форма. Обычная запись суммы (x+y) и произведения (x*y) является инфиксной формой. Примеры функций двух аргументов даны в таблице 5.3.

Функции, вводимые пользователем, также могут быть записаны в разных формах.

Получить информацию о любой функции можно с помощью команды: ?заголовок функции.

Напомним полезную команду меню Edit – Complete Selection (Ctrl+K), позволяющую автоматически закончить начатое слово. Достаточно написать начало слова и нажать клавиши Ctrl+K – появится список слов, из которого можно выбрать нужное слово, просто щелкнув на нем мышкой.

6

Таблица 5. 3 Функции

Нескольких аргументов

Standard form	Infix form
Plus[x,y]	x+y
Times[x,y]	x y
Power[x,y]	xy

. Функции комплексного аргумента

Перечисленные в предыдущем разделе функции применимы также и к комплексному аргументу. Дополнительные функции комплексного аргумента:

Re[z], Im[z] - действительная и мнимая части числа z,

Arg[z] - аргумент числа z.

Пример 6.1

In[ ] := Abs[1+I] Out[] =

In[ ] := Cos[I] Out[] =

In[ ] := Sqrt[2I] Out[] = In[ ] := Log[I] Out[] =

In[ ] := E^(I ) Out[] = -1 In[ ] := Arg[1+I] Out[] =

Замечание 1. В ряде случаев Математика по умолчанию не упрощает выходные выражения. Например, входное выражение Математика просто переписывает в ином виде. Для упрощения выражений можно применить функцию ComplexExpand[expr] – вычисление всех степеней и произведений в выражении expr – либо где-нибудь в выражении expr поставить десятичную точку.

Пример 6.2. На языке пакета Математика напишем список из трех выражений для извлечения

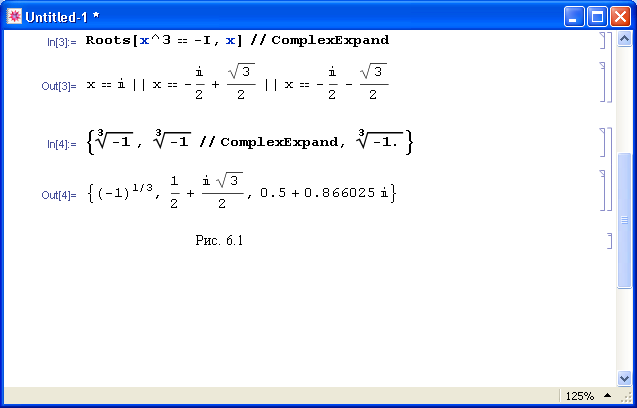
корня третьей степени:

Получим следующий ответ:

.

Замечание 2. При извлечении корня из комплексного числа Математика по умолчанию выдает значение корня с наименьшим (по абсолютной величине) значением аргумента.

Пример 6.3.

Найдем аргумент кубичного корня из –1 и –I. Запишем на языке пакета Математика:

Получим ответ:

Чтобы найти все n значений корня степени n можно воспользоваться функциями для решения уравнений Solve, FindRoot или Roots.

Пример 6.4. Найдем все значения корня третьей степени из –1 и –I:

In[] := Roots[x^3 == -1,x] //ComplexExpand,

Out [] = .

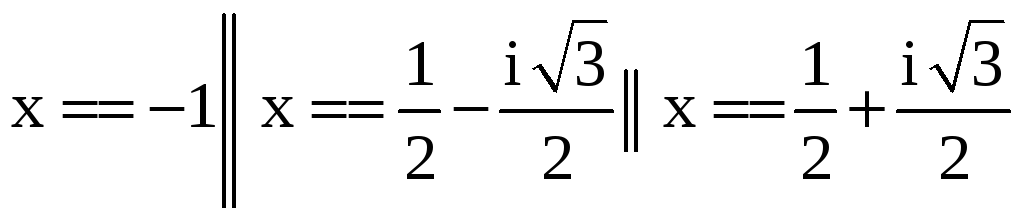In[] := Roots[x^3 == -I,x] //ComplexExpand,

Out [] = .
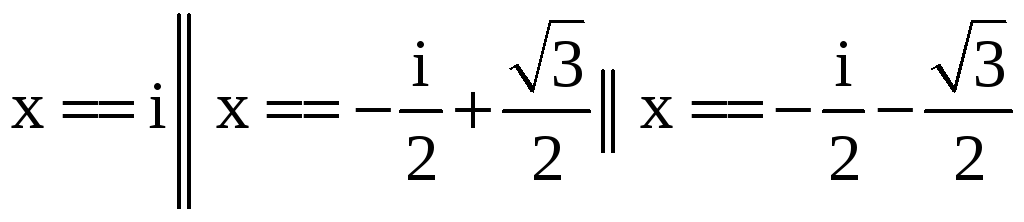