13.4. Решение дифференциальных уравнений

DSolve[ eqn, y[x], x ] – решает дифференциальное уравнение для функции y[x].

DSolve[{eqn₁, eqn₂,…}, {y₁[x], y₂[x],…}, x ] – решает систему дифференциальных уравнений.

Пример 13.16.

1). Общее решение.

In[ ] := DSolve[ y''[x] + y[x] == 0, y[x], x ]

Out[ ] = {{ y[x] –> C[2] Cos[x] – C[1] Sin[x] }}

2). Решение задачи Коши.

In[ ] := DSolve[{ y''[x] + y[x] == 0, y[0] == 1, y'[0] == 0 }, y[x], x ]

Out[ ] = {{ y[x] –> Cos[x] }}

3). Решение краевой задачи.

In[ ] := DSolve[{ y''[x] + y[x] == 0, y[0] == 0, y[5Pi / 6] == 1}, y[x], x ]

Out[ ] = {{ y[x] –> 2 Sin[x] }}

4). Решение краевой задачи для системы уравнений.

In[ ] := DSolve[{ y'[x] == z[x], z'[x] == -y[x], y[0] == 0, z[Pi] == -1}, {y[x], z[x]}, x ]

Out[ ] = {{ y[x] –> Sin[x], z[x] –> Cos[x] }}

NDSolve[ eqns, {y₁, y₂,…}, {x, xmin, xmax}] дает приближенное решение системы дифференциальных уравнений eqns на отрезке [xmin, xmax] для функций y_i[x]. NDSolve представляет решение на данном отрезке в виде интерполирующей функции InterpolatingFunction. Интерполирующая функция позволяет найти значения y для всех x, принадлежащих отрезку интерполяции, и построить график.

Пример 13.17. Найдем решение уравнения колебаний, описывающее затухающую синусоиду:

In[ ] := s = NDSolve[{ y''[t] + 0.1y'[t] +y[t] == 0, y[0] == 1, y'[0] == 0}, y, {t, 0, 20}]

Out[ ] = {{ y –> InterpolatingFunction[{{ 0., 20. }}, <>]}}

Решение представляется в виде интерполирующей функции. Построим график изменения и , а также “фазовый портрет” – зависимость . Для построения параментрического графика требуется использовать функцию Evaluate:

In[ ] := p1=Plot[{y[t]/.s, y'[t]/.s}, {t,0,20}, PlotStyle->{RGBColor[1,0,0],

RGBColor[0,0,1]}, AxesLabel->{t, y}];

p2=ParametricPlot[ Evaluate[{y[t], y'[t]}/.s], {t, 0, 20}, AxesLabel->{y,y'},

PlotStyle->RGBColor[1,0,1]];

Show[GraphicsArray[{p1,p2}]]

Г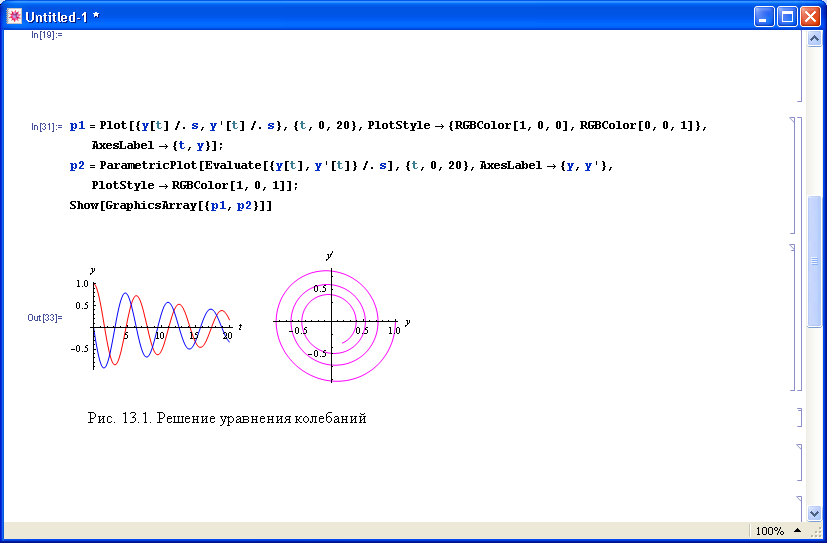рафики показаны на рис. 13.1.

Решение в виде интерполирующей функции позволяет найти значения и в любой точке отрезка, например:

In[ ] := {y[2Pi] /. s, y'[3Pi/2] /. s} Out[ ] = {{0.730093},{0.791057}}

Замечания

• Дифференциальные уравнения должны иметь достаточное количество начальных или краевых условий.

• Значение x₀, входящее в начальные или краевые условия, может не принадлежать отрезку [xmin, xmax].

• Уравнения могут включать комплексные числа.

14. Преобразование выражений

14.1. Стандартная форма выражений

В

Таблица 14.1

Примеры выражений

expr	FullForm
x + y + z	Plus[x, y, z]
x y z	Times[x, y, z]
x^n	Power[x, n]
{a, b, c}	List[a, b, c]
a -> b	Rule[a, b]
2 + I	Complex[2, 1]
f[x, y]	f[x, y]

се объекты, с которыми оперирует Математика, называются выражениями (Expression). Прототипом выражения является f[x,y]. Здесь f является заголовком (Head), а x и y – элементами выражения. В частности это выражение может описывать математическую функцию от двух аргументов f(x,y). В свою очередь x и y также могут быть выражениями.

Понятие выражения служит унифицирующим принципом Математики. То, что все объекты имеют подобную структуру, позволяет строить различные конструкции в разных областях применения с помощью сравнительно малого количества основных операций.

Хотя многие формулы могут быть выражены в разном виде, внутри пакета Математика эти формулы преобразуются в стандартную форму. Эту форму можно вывести на экран с помощью команды FullForm[expr]. Примеры выражений приведены в таблице 14.1. Обратим внимание, что стандартная форма записывается в виде: Заголовок[аргумент1, аргумент2,…], – где заголовок описывает основное действие, объединяющее аргументы.