Критерій Пірсона

Критерій ґрунтується на порівнянні теоретичних і емпіричних частот. Нехай область реалізацій випадкової величини розбито на k інтервалів, частоти яких дорівнюють   Якщо гіпотеза про закон розподілу в сукупності правильна, то можна обчислити ймовірності  тобто ймовірність потрапляння випадкової величини на i-й інтервал. Теоретичні частоти потрапляння нa цей інтервал можна розглядати як математичне сподівання компонентів випадкової величини, розподіленої за поліноміальним законом:

 

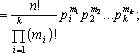
Статистичною характеристикою гіпотези є вибіркова функція  Якщо , то вибіркова функція має розподіл  з  ступенями волі, де r — кількість параметрів, оцінки для яких знайдено за вибірковими даними. Критична область для статистичної характеристики правостороння.

Критерій Колмогорова

Критерій ґрунтується на порівнянні статистичної і теоретичної функцій розподілу. Якщо

то при 

де  За допомогою таблиць розподілу Колмогорова визначається правостороння критична область.

 

Задача 71. Побудувати найпотужніший критерій для перевірки гіпотези  за альтернативної гіпотези , якщо вибірку обсягом n зроблено з нормально розподіленої сукупності з дисперсією, що дорівнює  Дібрати таке значення С, при якому a = 0,02, якщо  Яка з гіпотез прий- мається, якщо ?

Розв’язання. Застосуємо нерівність із теореми Неймана — Пір- сона:  Побудуємо функції правдоподібності:

 

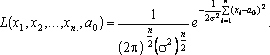
Підставимо функції правдоподібності в нерівність і виконаємо спрощення скороченням сталих множників. Дістанемо нерівність , яку прологарифмуємо і виконаємо низку перетворень:

  

 бо за умовою  Після заміни  остаточно дістанемо 

Отже, статистичною характеристикою гіпотези є вибіркова функція  а критичною областю для неї — множина значень, не менших за  Щоб дібрати значення С, потрібно знати закон розподілу вибіркової функції. Якщо справджується гіпотеза , то вибірку зроблено з нормально розподіленої сукупності з  Тоді  Центруємо і нормуємо вибіркову функцію, щоб застосувати таблиці функції Лапласа. Аналогічні перетворення виконуємо з правою частиною нерівності:   Критична область правостороння, тому її межа   Отже,   

Якщо , то  не належить критичній області і гіпотеза  приймається.

Задача 72. Із нормально розподіленої сукупності зроблено вибірку обсягом n = 15. За рівня значущості  перевірити гіпотезу  при альтернативній гіпотезі  якщо 

 

Розв’язання. Статистичною характеристикою гіпотези є вибір- кова функція  розподілена за законом  з n – 1 ступенями волі. Критична область лівостороння, бо  (рис. 24).

 

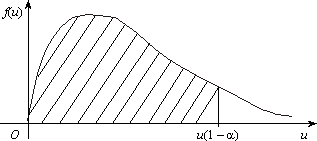
Рис. 24

Межу критичної області знаходимо за таблицями розподілу  при 14 ступенях волі.  Реалізація вибіркової функції 

Значення функції належить критичній області, отже, гіпотеза  відхиляється на користь альтернативної гіпотези 

Список використаної літератури

1. Барковський В.В. Математика для економістів. Теорія імовірності та математична статистика. К.: Національна академія управління, 1999. – 447с

2. Колемаев В.А. Теории вероятностей и математическая статистика. – М.: Висш. Школа, 1991. – 400с

3. Лавренчук В.П. Вища математика. Частина 2: Навч. посіб. – Чернівці: Рута, 2002. – 208с

4. Нікітін А.В. Статистика: навч.посіб. – Чернівці: Рута, 2011. – 124с

5. Мацкевич И.П. Сборник задач и упражнений по высшей математике: Теория вероятностей и математическая статистика. – Мн.: Выш. Школа, 1996. – 318с.