§ 5 Ряд Лорана

1. Означення і область збіжності ряду Лорана. Сума вигляду (2.6) називається рядом Лорана. Для з'ясування області збіжності цього ряду розглянемо його у вигляді двох сум:

.

Користуючись теоремою Абеля, з'ясовуємо, що частина ряду має область збіжності внутрішню частину круга радіусом . Розглянемо іншу частину ряду і введемо заміну , та отримаємо: . Даний ряд є степеневим із додатними степенями , тому його збіжність буде також реалізуватись всередині круга радіусом .

,

Якщо об'єднати обидва співвідношення, для збіжності ряду Лорана, необхідно, щоб одночасно виконувались обидві умови:

.

2. Подання аналітичної функції у вигляді ряду Лорана. Теорема: Нехай функція є аналітичною у круговому кільці , тоді вона може бути подана у вигляді ряду Лорана, причому таке подання буде однозначним:

.

Доведення: Розглянемо деяку точку з середини кругового кільця і оточимо двома колами, а саме внутрішнім і зовнішнім , , причому і , та запишемо інтеграл Коші по кривих, які співпадають із колами , :

.

Розглянемо другий доданок: :

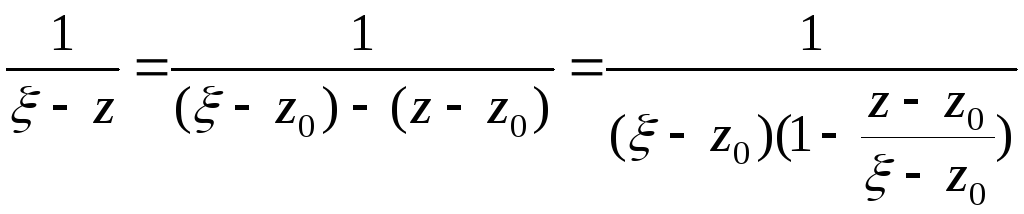
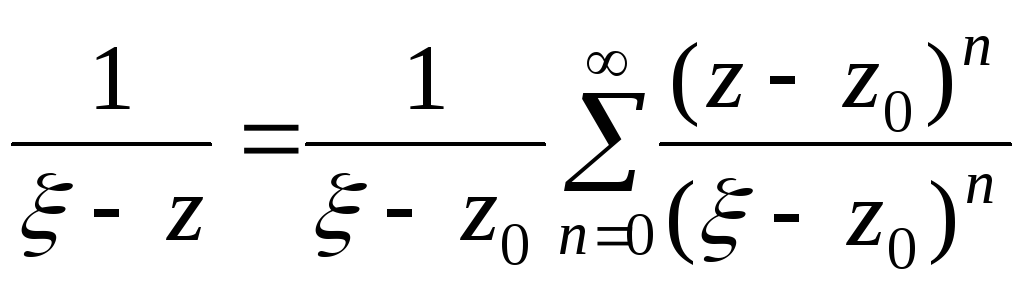, , то відповідно:

,

Розглянемо перший доданок: :

,

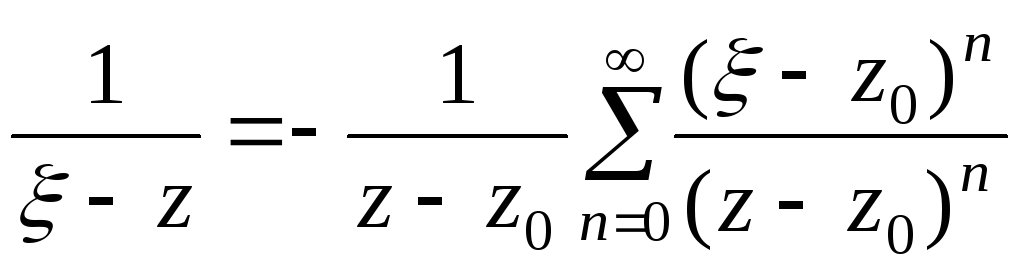, , то відповідно:

.

Якщо об'єднати два доданки, то ми можемо записати єдиний вираз для коефіцієнтів ряду Лорана:

, де – довільний контур у коловому кільці.

Отже, якщо функція є аналітичною в деякому круговому кільці, то її можна єдиним чином подати у вигляді ряду Лорана, у випадку коли .

§ 6 Класифікація ізольованих особливих точок аналітичної функції.

1. Означення ізольованих особливих точок. Точка є ізольованою точкою, якщо функція аналітична в області , а є особливою точкою цієї функції.

Приклад: , – є особливою точкою.

Класифікацію ІОТ (ізольованих особливих точок) здійснюється із використанням ряду Лорана .

а) ряд Лорана не містить від'ємних степеней ():

. В цьому випадку точка називається усувною ІОТ, і ;

б) точка є полюсом n-го порядку:

.

Отже при , ;

в) ряд Лорана містить безліч від'ємних степеней то точка є істотно ІОТ і при функція необмежено зростає.

ІОТ може бути також точка . Класифікація ІОТ здійснюється по вигляду ряду Лорана.

а) точка є ІОТ, якщо розклад ряду Лорана не містить додатній степеней, ;

б) точка є полюсом n-го порядку, якщо розклад ряду Лорана містить n-у найменшу додатну степінь ;

в) точка є істотно особливою точкою якщо розклад містить безліч додатних степеней .

Розділ №3. Теорія лишків

§1 Лишок аналітичної функції в ізольованій точці

Лишком аналітичної функції в точці називається інтеграл вигляду:

, (3.1)

де контур, що охоплює одну єдину ІОТ .

(3.2)

Формули (3.1) і (3.2) використовуються для обчислення лишків, але можна обчислити лишки не розкладаючи у ряд Лорана.

Приклад: а) нехай точка є полюсом 1-го порядку. Тоді

Знайдемо С_–1. для цього

, і спрямуємо :

.

Нехай , , а – має нуль першого порядку в точці . Тоді

.

б) нехай точка є полюсом m-го порядку:

Домножимо і візьмемо похідну , далі спрямуємо ,

Формула для обчислення лишку в полюсі m-го порядку наступна:

.

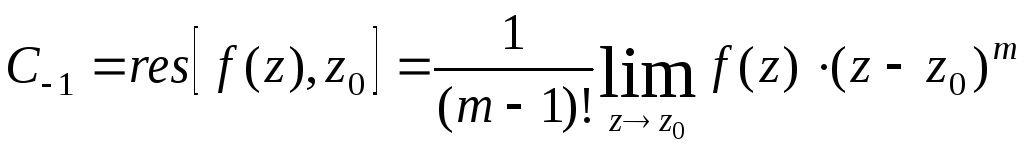Якщо точка є ІОТ, то лишком в цій точці називається інтеграл вигляду:

,

де контур охоплює всі ІОТ скінченої площини, якщо вони є, і виділяє одну єдину ІОТ .

Теорема 3.1 (основна теорема теорії лишків): Нехай функція аналітична в деякій області всюди, за винятком скінченого числа ІОТ , тоді інтеграл:

,

де контур, який охоплює ІОТ (без доведення).

Теорема 3.2: Якщо аналітична в комплексній площині всюди за винятком скінченого числа ІОТ (), тоді сума всіх лишків (без доведення).