§ 5 Інтеграли по комплексній змінній

1. Означення та основні властивості. Нехай на комплексній площині задана кусково-гладка крива кінцевої довжини . Використовуючи параметричне представлення кривої , заданим координатам і кожної її точки рівність , , де і кусково-гладкі функції дійсного параметра , який змінюється в межах ( і можуть відповідно набувати значення ±), що задовольняють умову . Задання координат , точок цієї кривої еквівалентне заданню комплексної функції дійсної змінної .

Нехай в кожній точці кривої визначено значення функції . Розіб’ємо криву на частинних дуг точками ділення , що відповідають зростаючим значенням параметру (). Введемо позначення та складемо суму:

, (1.5)

де – деяка точка і-той частинної дуги.

Якщо при існує границя сум (1.5), яка не залежить від способу розбиття кривої та вибору внутрішніх точок , то ця границя називається інтегралом від функції по кривій і позначається як:

. (1.6)

Записавши, що , , де – точка кривої на площині , ми можемо представити (1.5) вираження у вигляді:

.

. (1.7)

Властивості інтегралів по комплексній змінній:

1⁰ ;

2^{0 ;}

3⁰ ;

4⁰ , де – елемент довжини дуги;

5⁰ , де ;

6⁰ .

2. Теорема Коші. Оскільки значення контурного інтегралу залежить від напрямку інтегрування, домовимось в якості додатного напрямку обходження контуру брати напрям, при якому внутрішня область обмежена даним контуром, залишається зліва при обході контуру. Інтегрування в додатному напрямку будемо позначати через символ або просто , а інтегрування у від’ємному напрямку через – . Властивості інтегралів по замкнутому контуру від аналітичних функції всередині області, що обмежена даним контуром визначаються відомими властивостями криволінійних інтегралів першого роду. Як відомо для криволінійних інтегралів по замкнутому контурі має місце наступне твердження: якщо функції і неперервні в замкнутій області , яка обмежена кусочно гладким контуром , а їх частинні похідні першого порядку неперервні в області , то:

. (1.8)

Теорема 1.5 (теорема Коші). Нехай в однозв'язній області задана аналітична функція . Тоді інтеграл від цієї функції по довільному замкнутому контуру , що повністю лежить в цій області, рівний нулю.

Доведення: Згідно з формулою (1.7):

.

Так як функція аналітична всюди всередині конура , то функції та в області, яка є обмежена цим контуром, володіють неперервними частинними похідними першого порядку. Тому до криволінійних інтегралів, що стоять зліва можна застосувати формулу (1.8):

,

,

що і треба було довести.

Теорема 1.6 (друге формулювання теореми Коші). Якщо функція є аналітичною функцією в однозв'язній області , яка обмежена кусково-гладким контуром і неперервна в замкнутій області , то інтеграл від даної функції по границі області рівний нулю (без доведення).

Теорема 1.7 (третє формулювання теореми Коші). Нехай функція є аналітичною функцією в багато зв'язній області , яка обмежена ззовні контуром , а в середині контурами і нехай функція неперервна в замкнутій області , тоді , де повна границя області , що складається з контурів , причому обхід границі здійснюється в додатному напрямку.

Доведення: Проведемо гладкі криві , що з'єднують контур зі контурами (Рис. 4). Тоді область, що обмежена кривими та кривими , що проходять два рази в протилежних напрямках, виявляється однозв'язною. В силу теореми 1.6 інтеграл по границі цієї області рівний нулю .

Рис. 4.

3. Невизначений інтеграл. Важливим наслідком теореми Коші є наступне положення. Нехай функція є аналітичною функцією в однозв'язній області . Фіксуємо в цій області деяку точку і позначимо через інтеграл по довільній кривій, що повністю лежить в області і з'єднує точки і . В силу теореми Коші цей інтеграл не залежить від вибору кривої інтегрування в області і є однозначною функцією :

.

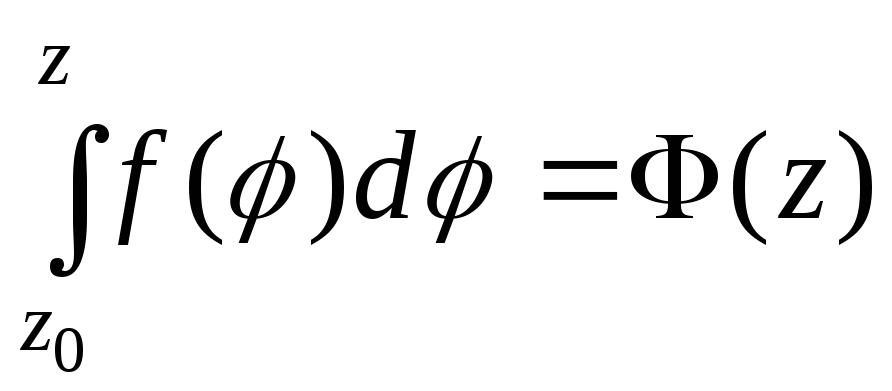Теорема 1.8. Нехай функція є визначеною і неперервною в деякій області , а інтеграл від цієї функцією по будь-якому контуру , який повністю лежить в даній області, рівний нулю. Тоді функція () є аналітичною функцією в області і (без доведення).

. (1.9)

(1.9) – формула Ньютона – Лейбніца. Це за умови, що – не виходить за межі області аналітичності функції.