§ 6 Інтеграл Коші

1. Виведення формули Коші. Нехай функція є аналітичною в однозв'язній області , яка обмежена контуром . Візьмемо довільну точку і побудуємо замкнутий контур , який повністю лежить в і всередині якого лежить точка . Розглянемо допоміжну функцію:

. (1.9)

Функція , очевидно, є аналітичною функцією у всіх точках області , за виключенням точки . Тому, якщо ми в області візьмемо деякий замкнутий контур , який лежить в середині , і так щоб точка попала в середину області, яка обмежена контуром , то функція буде аналітичною в двозв'язній області , яка є замкнутою між контурами і . Згідно з теоремою Коші інтеграл від по кривій рівний нулю:

.

Змінивши напрямок інтегрування в другому інтегралі, цю рівність можна переписати у вигляді:

. (1.10)

Оскільки інтеграл, що знаходиться зліва, не залежить від вибору контуру , то цією властивістю володіє і інтеграл, що знаходиться справа співвідношення (1.10). В подальшому, для зручності розглянемо в якості контуру інтегрування коло з радіусом і центром в точці (Рис.5).

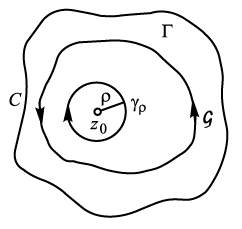
Рис. 5.

Підставивши , то отримаємо:

.

Інтеграл справа перетворимо так:

. (1.11)

Спрямуємо до нуля. Так, як аналітична, а відповідно є неперервною функцією в області , то для довільного числа можна поставити таке значення , що , для . Звідси випливає, що при існує границя:

.

Так, як у формулі (1.11) останній доданок не залежить від то , а відповідно, , то згідно (1.10):

. (1.12)

Інтеграл, що стоїть у правій частині формули (1.12), виражає значення аналітичної функції в деякій точці через її значення на довільному контурі , який лежить в області аналітичності функції і всередині якого розміщена точка . Цей інтеграл і називається інтегралом Коші. Формула (1.12) називається формулою Коші.

§ 7 Існування похідних всіх порядків аналітичної функції

1. Узагальнена формула Коші. Нехай дано функції та :

, (1.13)

де точка перебуває всередині контуру

. (1.14)

Маючи неповну інформацію про функцію , а саме її значення на деякій замкнутій кривій , ми можемо за допомоги формули (1.14) відновити цю функцію всередині деякої області , яка обмежена кривою .

Із (1.14) видно, що інтеграл який стоїть справа є аналітичною функцією змінної з області . Диференціюємо (1.14) по змінній :

. (1.15)

З (1.15) видно, що інтеграл справа є теж аналітичною функцією, тому ми можемо знову диференціювати співвідношення (1.15):

…

(1.16), де

Аналітичну функцію можна безліч раз диференціювати по її змінній . Аналітичною є функція, яка є безліч раз диференційованою в деякій області . Формула (1.16) називається узагальненою формулою Коші.

Розділ №2. Ряди аналітичних функцій

§1 Рівномірно збіжні функціональні ряди

1. Числові ряди. Сума вигляду (2.1) називається комплексним числовим рядом. Ряд (2.1) називається збіжним, якщо збігаються послідовності його частинних сум . При цьому границя послідовності називається сумою ряду (2.1).

Необхідною умовою збіжності ряду (2.1) є умова .

Згідно з ознакою Даламбера ряд вигляду (2.2) є збіжним, якщо, починаючи з деякого номеру , відношення , для всіх , а якщо починаючи з деякого номеру співвідношення , то ряд (2.1) з комплексними членами розбігається.

Згідно з ознакою Коші ряд (2.2) збігається, якщо , для всіх . Якщо ж починаючи з деякого номеру для всіх має місце відношення , то ряд (2.1) розбігається.

2. Рівномірно збіжні функціональні ряди. Сума вигляду: (2.3) називається функціональним рядом.

, де є сумою даного ряду.

Якщо члени функціонального ряду є мажорованими членами збіжного числового ряду, то даний функціональний ряд (2.3) є рівномірно збіжним.

Якщо (2.3) містить функції, які є аналітичними, і ряд є рівномірно збіжним, то його можна почленно диференціювати і інтегрувати:

;

.