14.5.6.1. Частное решение неоднородного уравнения

Частное решение неоднородного уравнения - ξ₂(t). Ищем ξ₂(t) в виде гармонической функции изменяющейся с частотой внешнего воздействия ω :

.

Первая и вторая производные от этой функции также будут гармоническими функциями, изменяющиеся с частотой ω. Значит, в уравнении 14.5.3.5, в левой его части, будет сумма трех гармонических функций одинаковой частоты, справа - гармоническая функция той же частоты, т.е. сумма трех колебаний одной частоты равна четвертому колебанию той же частоты. Задачу о сложении колебаний мы решим методом векторных диаграмм (14.3.1.), для этого и , после нахождения этих производных, запишем с помощью функции косинуса:

.

14.5.6.1.1. Векторная диаграмма

Изобразим эти колебания с помощью векторов (14.3.1.), амплитуды которых получаются после умножения на 2β, а - ξ на ω²₀.

.

В отличие от (14.3.2) вправо направим вектор длиной ω²₀A, изображающий функцию ω²₀A · Cos( ωt - φ) , начальная фаза которой равна "минус фи".

14.5.6.1.2. Резонанс

Т.к. ,

то

.

Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - ω_рез - резонансной. Для определения ω_рез исследуем функцию A(ω) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω) . Возьмем от него производную по и приравняем к нулю:

,

откуда:

.

При 2β² > ω²₀ резонанс отсутствует ( ω_рез - мнимое число).

14.5.6.1.2.1. Амплитуда при резонансе

Амплитуда при резонансе получается при подстановке найденного выражения ω_рез в формулу для A(ω).

.

При β << ω₀:

.

При ω = 0 отклонение системы от положения равновесия

.

Найдем отношение A_рез / A₀при условии β << ω₀:

,

здесь Q - добротность.

Добротность показывает (при β << ω₀ ) во сколько раз амплитуда при резонансе больше смещения при ω = 0.

14.5.6.1.2.2. Резонансные кривые

График зависимости A(ω) при различных β носят название резонансных кривых.

β₁ < β₂ < β₃,    2β²₃ > ω²₀, в этом случае резонанса нет.

15.1. Основные определения

15.1.1. Что такое упругая волна?

Упругая волна - это процесс распространения колебаний в упругой среде. Характерное свойство волны - перенос энергии без переноса вещества.

15.1.2. Описание волны

Для описания волны надо ввести функцию, в общем случае - векторную, задающую смещение от положения равновесия каждой частицы упругой среды для любого момента времени. Обозначим эту функцию греческой буквой [кси]. Аргументами ее, в соответствии с вышесказанным, будут три пространственные переменные - x, y, z, задающие положение частицы (или радиус-вектор ), и время t, т.е.

.

15.1.3. Скорость движения частиц упругой среды

- это частная производная от смещения по времени, т.е.

,

с такой скоростью частицы среды колеблются около своих положений равновесия.

15.1.4. Продольные и поперечные волны

Обозначим через скорость распространения волны. Если направление смещения (и скорость частицы ) совпадают с направлением скорости волны, то волна называется продольной. Если и взаимно перпендикулярны, то волна поперечная.

15.1.5. Фронт волны

- поверхность, отделяющая часть пространства, охваченную волновым процессом, от той части, где колебания не возникли.

15.1.6. Волновая поверхность

- это геометрическое место точек, колеблющихся в одинаковой фазе.

15.1.7. Плоская и сферическая волны

Плоская волна - волновые поверхности - плоскости. Сферическая волна - волновые поверхности - сферы. В общем случае форма волновых поверхностей может быть любой.

15.1.8. Длина волны

- это расстояние, на которое распространяется волна за один период колебаний.

       см. (3.9),

Так как (14.1.1.3)        ,

то                                  или     .

15.2. Уравнение плоской волны.

Пусть в начале координат находится твердая плоскость, которая колеблется по гармоническому закону и вынуждает частицы упругой среды, находящейся рядом с ней, колебаться по этому же закону. Направим ось x перпендикулярно этой плоскости. Тогда вдоль этой оси будет распространяться плоская гармоническая продольная волна. Наша задача - найти - уравнение волны, если задано .

Колебания до волновой поверхности, удаленной от начала координат на расстояние x, дойдут через время , значит уравнение волны

.

15.2.1. Фаза волны

- это аргумент у косинуса в уравнении волны, т.е.

,

Фаза плоской волны зависит от двух переменных - x и t.

15.2.2. Фазовая скорость

- это скорость перемещения в пространстве поверхности, вдоль которой фаза волны (15.2.1) остается постоянной, т.е.

.

Найдем производную от этого выражения по времени:

,

откуда искомая фазовая скорость волны:

.

15.2.3. Уравнение плоской волны,

распространяющейся в направлении, противоположном оси x:

.

Из (15.2.2) для этой волны:

.

15.2.4. Волновое число, симметричная форма уравнения волны

.

Введем

   - волновое число.

Тогда

.

При такой записи координата х и время t входят в уравнение волны симметрично.

15.2.4.1. Связь волнового числа с длиной волны

.

15.2.5. Уравнение плоской волны, распространяющейся в произвольном направлении. Волновой вектор

,

здесь - волновой вектор,

        - скалярное произведение волнового вектора и радиус-вектора.

15.3. Волновое уравнение

Применяя второй закон Ньютона (4.6) к упругой среде, можно получить дифференциальное уравнение в частных производных, решением которого будет уравнение волны. Логическая схема этого вывода такова:

15.3.1. Вывод закона Гука для бесконечно малого упругого стержня

Выделим элемент упругого стержня, длиной Δx.

Закрепим левую часть этого элемента (второй рисунок), правую сместим на величину Δξ вдоль оси x.

- закон Гука.

Здесь коэффициент k_упр, характеризующий упругость стержня, зависит от материала стержня, его длины и площади сечения.

15.3.1.1. Нормальное напряжение и относительная деформация

Введем:

     - нормальное напряжение,

       - относительная деформация.

При Δx → 0

.

Перепишем , выразив F и Δξ через σ и ε :

или

.

15.3.1.2. Модуль Юнга

Величина не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала:

.

15.3.1.3. Закон Гука

Тогда связь нормального напряжения σ и относительной деформации ε будет иметь вид:

.

Это выражение тоже носит название закона Гука.

15.3.2. Вывод волнового уравнения из .

Пусть волна распространяется вдоль упругого стержня. Рассмотрим элемент этого стержня, его длина равна Δx в невозмущенном состоянии. Пусть при распространения волны левая часть этого элемента сместится на величину ξ(x), а правая - на величину ξ(x + Δx), не равную смещению левой части.

.

В нашем примере стержень растянут внешними силами:

Сумма этих сил равна:

.

Домножим и поделим последнее выражение на Δ x. Величина

при Δx → 0 дает вторую производную от "кси" по x, т.е. .

Тогда .

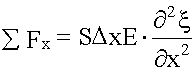Масса нашего элемента , его ускорение (3.10)

,

тогда преобразуется в

,

или

   - волновое уравнение.

Проверим, будет ли его решением.

Откуда

.

Т.к. (15.2.4), то фазовая скорость упругой продольной волны:

,

и волновое уравнение можно записать в виде:

.

Для волны, распространяющейся в произвольном направлении (15.2.5) волновое уравнение имеет вид:

.

15.4. Энергия упругой волны

Найдем полную механическую энергию (5.8.2) для выделенного нами элемента упругой среды, в которой распространяются упругая продольная волна:

.

Скорость (3.8.2):

,

тогда

.

Потенциальная энергия упругого деформированного стержня:

.

Полная энергия выделенного элемента объемом SΔx будет равна:

.

15.4.1. Плотность энергии упругой волны

.

15.4.1.1. Плотность энергии упругой гармонической волны

15.4.1.1.1. Среднее по времени значение плотности энергии упругой гармонической волны

, это известно из математики, значит:

.

15.4.2. Поток энергии

15.4.3. Плотность потока энергии

15.4.4. Вектор Умова - связь плотности потока энергии с плотностью энергии упругой волны

15.4.5. Интенсивность волны

- это среднее по времени от модуля вектора плотности потока энергии:

.

Для гармонической волны:

.

15.5. Стоячие волны

При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит.

15.5.1. Уравнение стоячей волны

Для волны, бегущей по оси x:

.

Для волны, бегущей против оси x:

,    см. (15.2.3), (15.2.4), (15.2.5).

Для простоты мы положили равным нулю значение начальных фаз этих волн. Сумма этих уравнений и дает уравнение стоячей волны:

15.5.1.1. Амплитуда стоячей волны

- это модуль выражения, стоящего перед множителем Cosωt, т.е.

15.5.2. Узлы и пучности

Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:

Следовательно, координаты узлов:

Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны.

Для пучностей:

Координаты пучностей:

15.5.3. Колебания струны, закрепленной с двух концов

В силу граничных условий, заданных закреплением концов струны, уравнение стоячей волны при выборе начала координат на одном из концов струны следует записать через функцию Sin kx, т.е.

.

Тогда условие будет выполнено. Для выполнения граничного условия на другом конце струны мы должны потребовать, чтобы

.

Это приводит к квантованию волнового числа, т.е. k может принимать не любые значения, а только дискретные, определяемые равенством:

т.к.

то

Вдоль струны должно укладываться целое число полуволн! Из (15.1.7) и мы получаем спектр (набор) частот, на которых может колебаться закрепленная с двух концов струна:

Частота v₁ называется основным током,     v₂ - первым обертоном и т.д.