3. Угол между двумя прямыми.

и вычисляется по формуле:

3. Условия параллельности и перпендикулярности прямых в пространстве. Расстояние точки до прямой.

1) Пусть даны две прямые

Д

анные прямые параллельны в том и только в том случае, когда их направляющие векторы ; коллиниарны следовательно получаем условие параллельных двух прямых:

2) Данные прямые перпендикулярны в том и только в том случае, когда их направляющие векторы перпендикулярны (в пространстве эти прямые могут быть и не пересекающимися) следовательно получаем условие перпендикулярности двух прямых:

3) Расстояние от точки до прямой.

Е

сли прямая задана уравнением , можем найти расстояние h от точки с радиус – вектором R до прямой, разделив S параллелограмма, построенного на векторах R – r₀ и a, на длину его основания. Результат можно записать формулой:

3. Взаимное расположение прямой в плоскости:

• угол между прямой и плоскостью;

Для вычисления угла прямой и плоскости определяют угол Q между направляющим вектором прямой и вектором, перпендикулярным к плоскости, и по нему находят искомый угол. Если направляющий вектор прямой выбрать так, чтобы , и взять , то угол между прямой и плоскостью дополняет Q до .

• условие параллельности и перпендикулярности;

Пусть прямая задана уравнением , а плоскость – одним из уравнений . Прямая параллельная плоскости (а возможно, и лежит в плоскости), если (a, n) = 0 или (a, p, q) = 0. Если плоскость, задана линейным уравнением , то, согласно предложению (любые две неколлинеарных вектора, компоненты которых удовлетворяют уравнению , могут быть приняты за направляющие векторы плоскости, имеющей уравнение в общей декартовой системе координат) компоненты a₁, a₂, a₃, направляющего вектора прямой, параллельные плоскости, должны удовлетворять уравнению: (1).

В декартовой прямоугольной системе координат это условие совпадает с (a, n) = 0.

Пусть прямая линия задана двумя линейными уравнениями: , тогда по предложению (вектор с компонентами будет направляющим вектором прямой какова бы не была декартовая система координат) можно положить: , и условие (1) переписывается в виде:

(2).

Л

егко проверить, что все приведенные здесь условия являются не только необходимыми, но и достаточными. Из формулы (2) следует, что три плоскости пересекаются в одной точке тогда и только тогда, когда коэффициенты удовлетворяют условию:

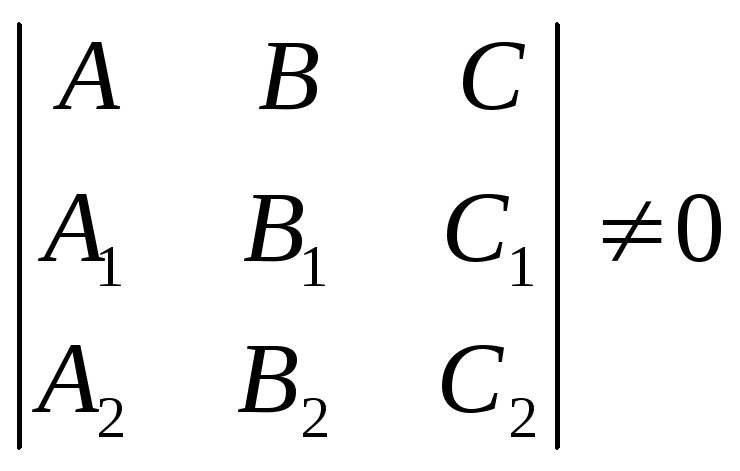
Действительно, это неравенство означает, что прямая линия, по которой пересекаются какие – нибудь две из плоскостей, не параллельны третьей плоскости.

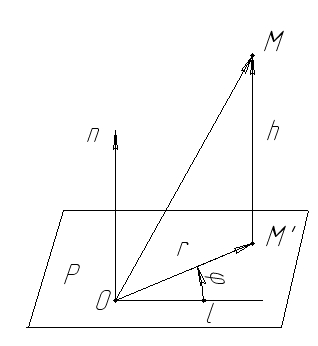
Цилиндрические и сферические координаты.

В пространстве обобщением полярных систем координат являются цилиндрические и сферические системы координат. И для тех, и для других фигура, относительно которой определяется положение точки, состоит из точки 0, луча l, исходящего из 0 и вектора n, неравному по длине единице и перпендикулярному к l. Через точку 0 можем провести плоскость P, перпендикулярную вектору n.

Пусть дана некоторая точка М. Опустим из ее перпендикуляр на плоскость P.

Цилиндрические координаты точки M(r,, h), числа r, - полярные координаты, точка по отношению к полуоси 0 и полярной оси l, а h – компонента по вектору n. Она определена, так как эти векторы коллиниарны.

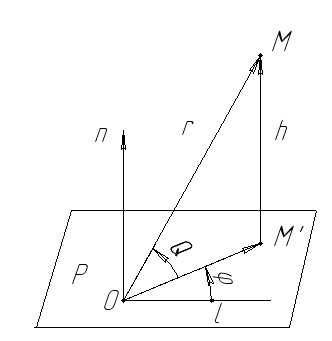
Сферические координаты точки (r,, Q). Они определяются так: ; как и для цилиндрических координат  - углов вектора, с лучом l; и Q – угол с плоскостью P.