3. Угол между двумя плоскостями.

Зададим две плоскости:

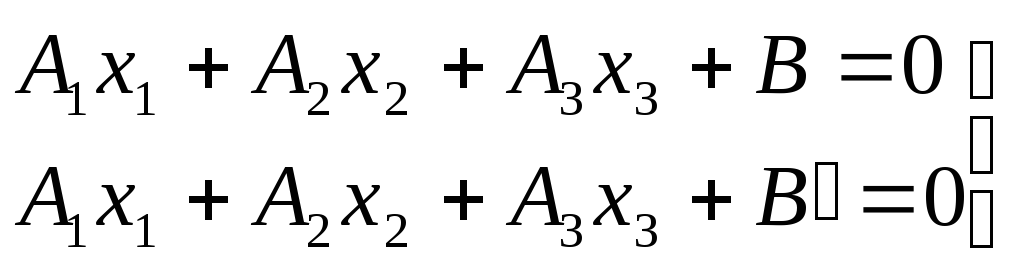(1)

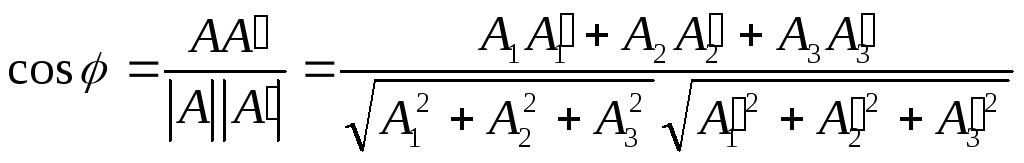
и перпендикулярны соответственно данным плоскостям, поэтому угол  м\у А и равны углу (двугранному) м\у …………. Плоскостями. Но скалярное произведение: , поэтому

(2)

Достаточно считать, что . Две пересекающиеся плоскости на самом деле образуют два двугранных угла ₁ и ₂. Их сумма равны π (₁ + ₂ = π), а их cos равен по абсолютной величине, но отличаются знаками (cos ₁ = - cos₂ ). Если заменить в уравнении (1) числа A₁, A₂, A₃ соответственно на числа -A₁, -A₂, -A₃, то полученное урвнение будет определять ту же плоскость, но угол  во (2) замениться на π - .

3. Условие параллельности и перпендикулярности плоскостей.

Условием перпендикулярности плоскостей (1) будет, очевидно, cos  = 0 т.е.

(3).

Две плоскости (1) параллельны тогда и только тогда, когда (перпендикулярные к ним) векторы А и коллинеарные, т.е. выполняются условия пропорциональности:

(4).

Е

сли дополнительно к этому выполняется расширенное условие пропорциональности

(5),

то это говорит о том, что плоскости (1) совпадают, т.е. оба уравнения (1) определяют одну и ту же плоскость.

Хотя на 0 делить нельзя, но удобно писать символические пропорции (4) или (5) с 0, в знаменателях. Но тогда, если, например, А₂ = 0 , то надо считать, что и = 0. Или, если , то В = 0.

3. Расстояние от точки до плоскости.

Требуется найти расстояние от точки до плоскости L, определяемой уравнением . Для этого приведем уравнение L к нормальному виду .

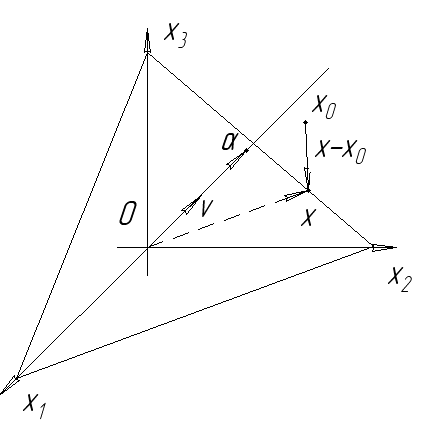
Разность х – х⁰ радиус - вектора произвольной точки х плоскости L и радиус – вектора точки х⁰ есть такой вектор, что абсолютная величина его проекции на v равна искомому расстоянию d от х₀ до  :

, но

Д

ля того, чтобы вычислить расстояние в от точки х⁰ до L, надо записать уравнение L в нормальном виде, перенести Р в левую часть и подставить в последнюю х⁰ вместо х. Абсолютная величина полученного выражения и есть искомое число d

.

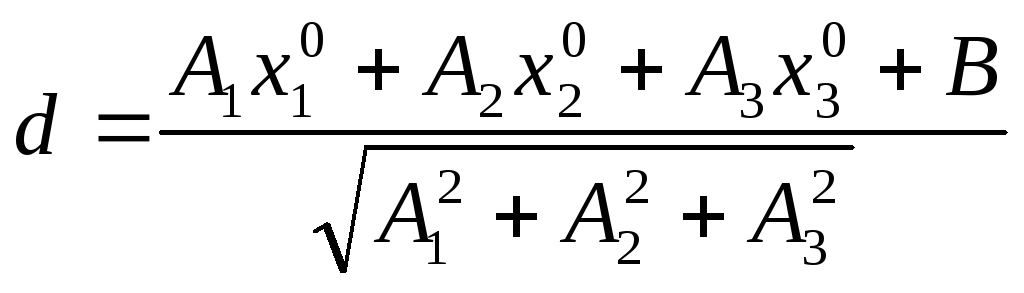
Если точки х₀ и (0; 0) находятся по разные стороны от плоскости L, то вектор х – х₀ образует с v тупой угол, следовательно .

Если все точки х₀ и (0; 0) находятся по одну сторону от L, то указанный угол острый, и тогда в первом случае а во

втором - .

3. Уравнения прямой:

• канонические уравнения;

Пусть дана какая – нибудь прямая. Каждый не равный 0 вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой. Указанные векторы называются направляющими потому именно, что любой из них, будучи задан, определяет направление прямой.

Направляющий вектор произвольной прямой будем обозначать буквой .

Выведем сейчас уравнение прямой, проходящей через данную точку M₀(x₀, y₀, z₀) и имеющей данный направляющий вектор .

Пусть М(x, y, z) любая («текущая») точка прямой.

калинеарен направляющему вектору следовательно, координаты пропорциональны координатам :

(1)

Этим соотношениям удовлетворяют координаты каждой точки М(x, y, z), лежащей на рассматриваемой прямой; напротив, если М(x, y, z) не лежат на этой прямой, то ее координаты не удовлетворяют соотношению (1), так как в этом случае векторы и не коллиниарны и координаты их не пропорциональны. Т.о. ,(1) представляют собой уравнение прямой проходящей через точку M₀(x₀, y₀, z₀) в направлении вектора . Уравнение прямой, полученного сейчас специального вида будем называть каноническими. Координаты l, m, n любого направляющего вектора и прямой называются направляющими параметрами этой прямой.

• параметрические уравнения;

Пусть даны канонические уравнения какой – нибудь прямой. Обозначим t каждое из равных отношений, которые участвуют в этих канонических уравнениях:

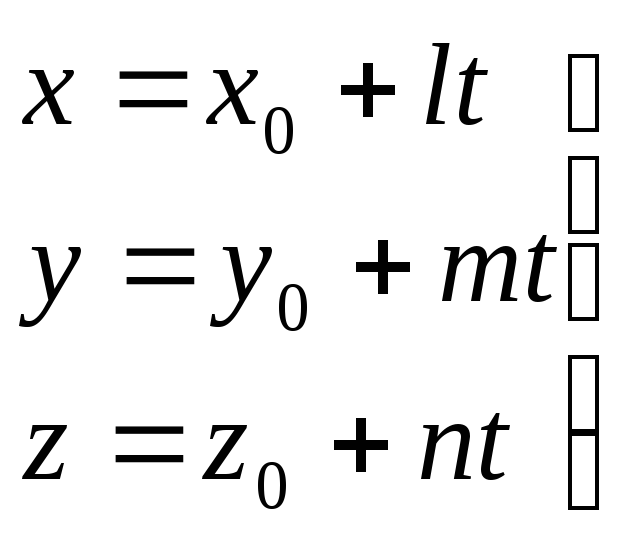
=> (2)

Это – параметрические уравнения прямой, проходящей через точку M₀(x₀, y₀, z₀) в направлении вектора . В уравнении (2) t рассматривается как произвольно изменяющийся параметр, x, y, я – как функции от t; при изменении t величины x, y, я меняются так, что точка М(x, y, z) движется по данной прямой. Параметрические уравнения прямой удобно применять в тех случаях, когда требуется найти точку пересечения прямой с плоскостью.