
- •Теоретические вопросы аналитическая геометрия на плоскости
- •1. Метод координат: числовая прямая, координаты на прямой; прямоугольная (декартовая) система координат на плоскости; полярные координаты.
- •Прямоугольная (или декартовая) система координат на плоскости.
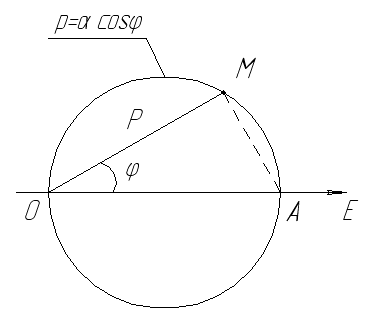
- •Полярные координаты.
- •4. Деление отрезка в данном отношении.
- •Доказательство.
- •5. Определение уравнения линии, примеры линии на плоскости.
- •6. Прямая линия на плоскости:
- •Доказательство.
- •7. Угол между двумя прямыми.
- •8. Условия параллельности и перпендикулярности двух прямых.
- •9. Взаимное расположение двух прямых на плоскости.
- •10. Расстояние от точки до прямой.
- •Доказательство.
- •11. Линии второго порядка:
- •Аналитическая геометрия в пространстве
- •Прямоугольная система координат в пространстве.
- •2. Уравнения поверхности и линии в пространстве.
- •Уравнение плоскости:
- •Доказательство.
- •Угол между двумя плоскостями.
- •Условие параллельности и перпендикулярности плоскостей.
- •Расстояние от точки до плоскости.
- •Уравнения прямой:
- •Угол между двумя прямыми.
- •Условия параллельности и перпендикулярности прямых в пространстве. Расстояние точки до прямой.
- •Взаимное расположение прямой в плоскости:
- •Цилиндрические и сферические координаты.
- •Поверхности второго порядка:
4. Деление отрезка в данном отношении.
![]()
Число λ, определяемое равенством ; называется отношением,
в котором, точка М делит отрезок М1М2.
Задача о делении отрезка в данном отношении состоит в том, чтобы по данному отношению λ и данным координатам точек М1 и М2 найти координаты точки М.
![]()
(5)
,
где (x1;y1) – координаты точки М1, (x2;y2) – координаты точки М2.
Доказательство.
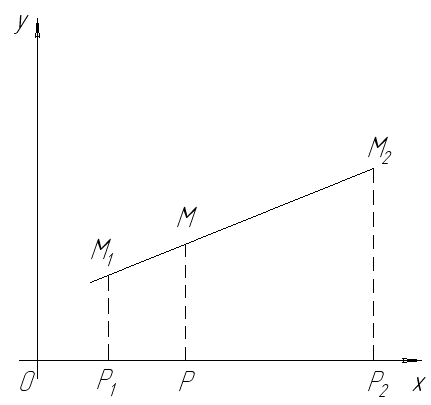
Пусть М1М2 не перпендикулярны оси OX. Опустим М1P OX, MP OX, М2Р2 ОХ.
На основании теоремы элементарной
геометрии о пропорциональности отрезков
прямых, законченных между параллельными
прямыми, имеем
![]() .
Но по теореме (если М1 (x1)
и M2(x2)
– любые две точи и α – расстояние
между ними, то
.
Но по теореме (если М1 (x1)
и M2(x2)
– любые две точи и α – расстояние
между ними, то
![]() )
)
![]() .
Так как числа (x - x1) и
(х2 - х) имеют один и тот
же знак (при х1<x2
они положительны, а при х1>x2
отрицательны), то
.
Так как числа (x - x1) и
(х2 - х) имеют один и тот
же знак (при х1<x2
они положительны, а при х1>x2
отрицательны), то
![]() .
Поэтому
.
Поэтому
![]() ,
откуда
,
откуда
![]() .
Если М1М2
OX, то x1
= x2=
x и эта формула
очевидно, верна. Вторая формула находится
аналогично.
.
Если М1М2
OX, то x1
= x2=
x и эта формула
очевидно, верна. Вторая формула находится
аналогично.
![]()
![]() ,
то λ=1 и по формулам (5) получаем:
,
то λ=1 и по формулам (5) получаем:
.
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат.
5. Определение уравнения линии, примеры линии на плоскости.
Рассмотрим соотношение вида F(x, y)=0, связывающее переменные величины x и у. Равенство (1) будем называть уравнением с двумя переменными х, у, если это равенство справедливо не для всех пар чисел х и у. Примеры уравнений: 2х + 3у = 0, х2 + у2 – 25 = 0,
sin x + sin y – 1 = 0.
Если (1) справедливо для всех пар чисел х и у, то оно называется тождеством. Примеры тождеств: (х + у)2 - х2 - 2ху - у2 = 0, (х + у)(х - у) - х2 + у2 = 0.
Уравнение (1) будем называть уравнением множества точек (х; у), если этому уравнению удовлетворяют координаты х и у любой точки множества и не удовлетворяют координаты никакой точки, не принадлежащие этому множеству.
Важным понятием аналитической геометрии является понятие уравнения линии. Пусть на плоскости заданы прямоугольная система координат и некоторая линия α.
α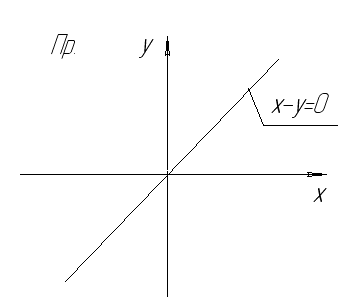
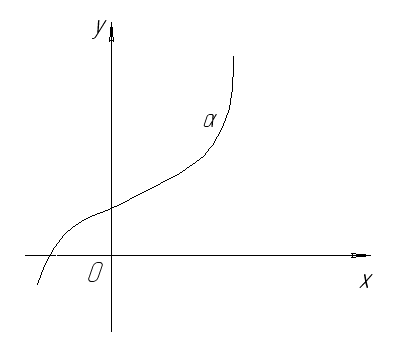
 Определение. Уравнение (1) называется
уравнением линии α ( в созданной
системе координат), если этому уравнению
удовлетворяют координаты х и у
любой точки, лежащей на линии α, и
не удовлетворяют координаты никакой
точки, не лежащей на этой линии.
Определение. Уравнение (1) называется
уравнением линии α ( в созданной
системе координат), если этому уравнению
удовлетворяют координаты х и у
любой точки, лежащей на линии α, и
не удовлетворяют координаты никакой
точки, не лежащей на этой линии.
Если (1) является уравнением линии α, то будем говорить, что уравнение (1) определяет (задает) линию α.
Линия α может определятся не только уравнением вида (1), но и уравнением вида
F (P, φ ) = 0, содержащим полярные координаты.
6. Прямая линия на плоскости:
-
уравнение прямой с угловым коэффициентом;
Пусть дана некоторая прямая, не перпендикулярная, оси ОХ. Назовем углом наклона данной прямой к оси ОХ угол α, на который нужно повернуть ось ОХ, чтобы положительное направление совпало с одним из направлений прямой. Тангенс угла наклона прямой к оси ОХ называют угловым коэффициентом этой прямой и обозначают буквой К.
К=tg α (1)
Выведем уравнение данной прямой, если известны ее К и величина в отрезке ОВ, которой она отсекает на оси ОУ.
x b
α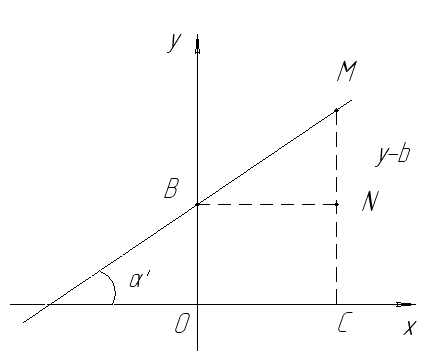
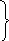
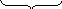

(2)![]() y=kx+b
y=kx+b![]() .
Но NM=CM-CN=CM-OB=y-b,
BN=x
=> учитывая
(1), получаем, что точка М (х; у) С на
данной прямой <=>,
когда ее координаты удовлетворяют
уравнению:
.
Но NM=CM-CN=CM-OB=y-b,
BN=x
=> учитывая
(1), получаем, что точка М (х; у) С на
данной прямой <=>,
когда ее координаты удовлетворяют
уравнению:
![]() =>
=>
Уравнение (2) называют уравнением прямой с угловым коэффициентом. Если K=0, то прямая параллельна оси ОХ и ее уравнение имеет вид y = b.
-
уравнение прямой, проходящей через две точки;
(4)![]()
![]() .
Это уравнение, если у1≠
у2, можно записать в виде:
.
Это уравнение, если у1≠
у2, можно записать в виде:
Если у1 = у2, то уравнение искомой прямой имеет вид у = у1. В этом случае прямая параллельна оси ОХ. Если х1 = х2, то прямая, проходящая через точки М1 и М2, параллельна оси ОУ, ее уравнение имеет вид х = х1.
-
уравнение прямой, проходящей через заданную точку с данным угловым коэффициентом;
y – y1
= k(x – x1) (3)
Замечание. Если прямая проходит через точку М1 (х1;у1) перпендикулярна оси ОХ, т.е. ее угловой коэффициент обращается в бесконечность, то уравнение прямой имеет вид
х – х1 = 0. Формально это уравнение можно получит из уравнения (3), если разделить (3) на k и затем устремить k к ∞.
-
общее уравнение прямой, частные случаи;
Аx + Вy
+ С = 0
(5)
и, обратно, уравнение (5) при произвольных коэффициентах А, В, С (А и В ≠ 0 одновременно) определяет некоторую прямую в прямоугольной системе координат Оху.
