Оценка случайной погрешности

При проведении повторных измерений одной и той же величины мы получаем результаты измерений, некоторые из которых отличаются по числовому значению друг от друга, а некоторые совпадают. Расхождения между результатами указывают на наличие случайных погрешностей , о природе и причинах возникновения которых сказано выше.

Нанесем результаты повторных измерений величины по мере их поступления на числовую ось (рис. 1.9). Маленькие кубики, показывающие число измерений, располагаются вдоль горизонтали в соответствии с измеряемыми значениями. Совокупность таких кубиков образует фигуру, называемую гистограммой. Она характеризует возможный разброс результатов измерений.

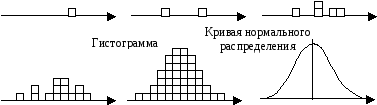
Рис. 1.9. Построение статистического распределения

При увеличении числа измерений можно увидеть следующее: несмотря на то, что сами значения изменяются, их распределение подчиняется некоторому правилу. В большинстве случаев это правило следующее: основная часть измеренных значений группируется около некоторого среднего значения, причем значения, близкие к среднему будут встречаться чаще значений, отличающихся от него, и чем больше отклонение, тем реже оно встретится.

Предположим, мы регистрируем все больше и больше данных. Тогда через некоторое время их распределение стабилизируется, и изменения с приходом все новых и новых измерений будут практически незаметны. Таким образом, гистограмма превращается в сглаженную кривую распределения. На рис. 1.9 показано наиболее часто встречающееся на практике распределение, называемое нормальным распределением.

Таким образом, совокупность большого числа результатов повторных измерений подчиняется определенным законам. При описании этих законов метрология использует математический аппарат теории вероятности. Теория вероятности рассматривает свойства случайных явлений, которые происходят при массовых событиях, т.е. в совокупности большого числа событий, к числу которых относятся и многократно повторяемые измерения. При этом результат измерения величины, содержащий случайную погрешность, а также саму случайную погрешность , рассматривают как случайную величину.

Для количественной оценки объективной возможности появления того или иного значения случайной величины служит понятие вероятности, которую выражают в долях единицы (вероятность достоверного события равна 1, а невозможного события – 0).

Нормальный закон распределения случайной величины. Параметры нормального распределения

Математическое описание непрерывных случайных величин (к числу которых относится и ), осуществляется обычно с помощью законов распределения случайной величины. Эти законы определяют связь между возможным значением случайной величины и соответствующей ему плотности вероятности.

Наиболее распространенным при измерениях является нормальный закон распределения (рис. 1.9). Он наблюдается, когда расхождения результатов обусловлены большим числом независимых причин и ни одна из них не доминирует над остальными. На рис. 1.10, а показана кривая нормального распределения для некоторой измеряемой величины Х. По оси абсцисс отложены значения величины Х, а по оси ординат – вероятность их появления р(Х). Кривая нормального распределения симметрична линии, проходящей через центр распределения M[Х] (математическое ожидание), и имеет колоколообразную форму. Рассеяние результатов отдельных измерений относительно центра распределения характеризуется средним квадратическим отклонением . Математическое ожидание M[Х] является тем значением величины, вокруг которого группируются результаты отдельных измерений.  является мерой рассеяния результатов относительно M[Х], т.е. характеризует форму кривой распределения.

а	б

Рис. 1.10. Кривые нормального распределения: а – случайной величины Х, б – случайной погрешности

Перенеся начало координат в точку M[Х], получим кривую распределения случайной погрешности (рис. 1.10, б).

На рис. 1.11 приведены кривые нормального распределения при различных значениях  (рассеяния результатов). Сравнивая их между собой, можно установить, что рассеяние для кривой 2 меньше, чем для кривой 3, но больше, чем для кривой 1. Очевидно, что наиболее высокая сходимость наблюдается для результатов измерений, распределенных в соответствии с кривой 1.

Рис. 1.11. Кривые нормального распределения с разным рассеянием значения величины, ₁  ₂  ₃

Математическое выражение для описания кривой нормального распределения случайной величины (рис. 1.10, а), предложенное Гауссом, имеет вид

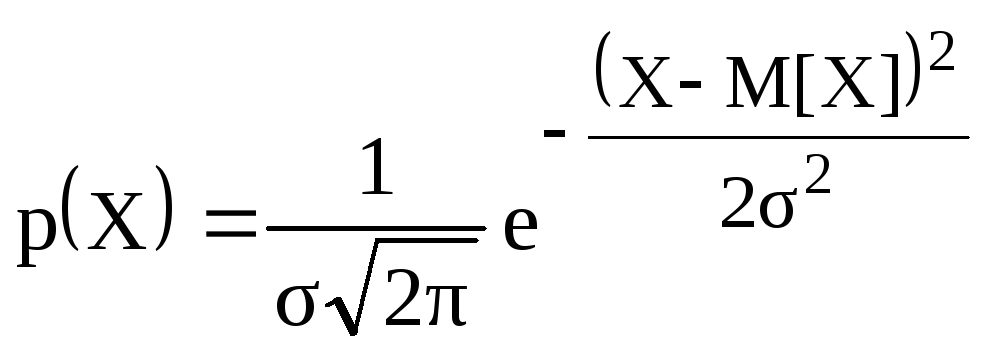(1.10)

Для описания кривой нормального распределения случайной погрешности (рис. 1.10, б) это выражение можно переписать в виде

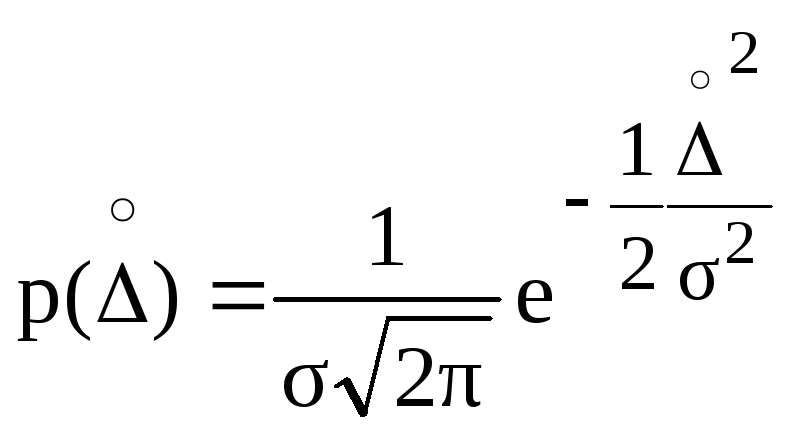(1.11)

M[Х] и  являются двумя важнейшими параметрами нормального распределения случайной величины. Достаточно знать эти параметры, чтобы задать нормальное распределение.