§6 Оптимальная норма накопления
В §5 был исследован вопрос
о поведении траектории однопродуктовой
макромодели в том случае, когда норма
накопления – заданная постоянная
величина. Эта норма может быть выбрана
различной по значению, что, разумеется,
сказывается на характеристиках роста
макроэкономических показателей.
Важнейшим из таких показателей с точки
зрения потребителя является удельное
потребление
.
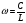Согласно формуле (15)
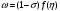(25),
где
- норма накопления,
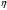- фондовооружённость.
Из полученных выше результатов следует, что при расчёте экономических показателей для достаточно больших значений времени может быть использован режим сбалансированного роста.
На траекториях
сбалансированного роста фондовооружённость
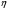постоянна, а значит, будет постоянным
и удельное потребление
.
Поставим перед собой задачу отыскания
таких значений
,
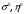при которых удельное потребление (25)
максимально. Величины
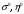называют оптимальной нормой накопления
и оптимальной фондовооружённостью.
Рассмотрим сначала
модель без учёта запаздывания при
освоении капиталовложений. В этом случае
норма накопления и фондовооружённость
при сбалансированном росте связаны
между собой уравнением (20). Таким образом,
мы приходим к задаче отыскания точки
максимума функции (25) при ограничении
(20) и естественных условиях
.
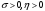Из уравнения (20) следует, что
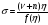(26)
Тогда удельное потребление как функция фондовооружённости задается формулой
(27)
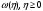имеет те же свойства,
что и (21), а именно, это строго вогнутая
функция, принимающая положительные
значения на некотором интервале
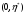(ссылка на старый рисунок, ТРИ).
Поскольку только
положительные значения
имеют экономический смысл, то
фондовооружённости
,
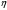которые возможны при сбалансированном
росте, заполняют интервал
.
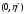То, что фондовооружённости не могут
быть сколь угодно большими на неформальном
языке можно объяснить следующим образом:
при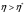
фонды должны возрастать слишком быстро.
Для этого потребуется настолько много
инвестиций, что они будут просто превышать
выпуск продукта.
Очевидно, максимум
функции
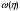достигается в единственной точке
,
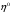которая является корнем уравнения
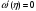или, что то же самое,
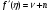(28)
Поскольку функция
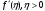убывает, это уравнение имеет единственный
корень. Согласно (26), оптимальная норма
накопления равна
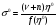(29).
Пусть
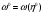- максимальное удельное потребление.
Заметим, что любое меньшее удельное
потребление достигается при двух
значениях фондовооружённости (или
накопления). Одно из них меньше
оптимального, а другое – больше (рисунок).
Обсудим это весьма интересное
обстоятельство.
Как уже отмечалось, фонды (капитал) предназначены для производства предметов потребления в будущем, представляя собой как бы отложенные потребления. Однако может случиться так, что фонды будут воспроизводить как бы самое себя, «забыв» о своем предназначении. Для наглядности рассмотрим следующую ситуацию: добывая уголь и руду, мы производим из них металл. Часть этого металла пойдет на производство ложек и вилок, часть - на производство машин для добычи угля и руды. Но те же ложки и вилки можно сделать гораздо меньшими усилиями, не добывая так много руды и угля и не производя поэтому так много машин для их добычи.
Итак, одно и то же потребление можно обеспечить при очень большом объёме инвестиций, которые предназначены прежде всего для усиления воспроизведения фондов, и при сравнительно малом объёме, когда фонды в таком количестве не создаются.
В случае функции
Кобба-Дугласа
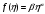уравнение (28) для нахождения оптимальной
фондовооружённости принимает вид
,
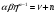откуда
,
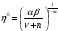то есть оптимальная
норма потребления
.
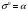В однопродуктовой модели
с запаздыванием (конспект семинарских
занятий) задача об оптимальной норме
накопления сводится к нахождению точки
максимума функции (25) в области
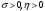при ограничении
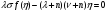(30)
Тогда удельное потребление как функция фондовооружённости имеет вид
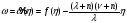(31)
Функция
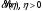отличается от (27) только коэффициентами
при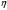
,
поэтому эти функции имеют одинаковые
свойства.
Оптимальная фондовооружённость
,
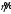доставляющая максимум функции (31),
является решением уравнения
или, что то же самое,
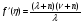(32)
Согласно (30), оптимальная норма накопления задается формулой
(33)
Как и в предыдущей модели,
если удельное потребление
меньше максимального
,
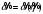то оно достигается при двух значениях
фондовооружённости (нормы накопления)
(рис ЧЕтыРЕ).
В случае функции Кобба-Дугласа уравнение (32) принимает вид
,
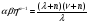откуда
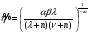
Подставив это значение
в (33), получим после преобразований
,
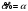что совпадает с оптимальной нормой
накопления в модели без запаздывания.
Заметим, что для других производственных функций такой факт, вообще говоря, не имеет место.