
- •1.8 Поняття рангу матриці.
- •1.11 Матричний запис слар
- •1.12 Розвязуання слар матричним способом
- •2.18 Базис на площині і в просторі. Розкладання вектора за базисом (на площині і в просторі).
- •2.19 Координати вектора. Довжина
- •2.20 Лінійні операції над векторами
- •2.23 Кут між векторами
- •2.24 Векторний добуток. Означення і властивості
- •2.26 Мішаний добуток
- •2.27 Міш добуток, що задані в координатній формі.
- •2.28 Геометричні застосування мішаного добутку.
- •2.29 Умова компланарності векторів
- •3.30. Прямокутна декартова система координат
- •3.31 Пряма на площині.
- •3.38 . Криві другого порядку. Означення, властивості та канонічні рівняння: еліпс; гіпербола; парабола
- •3.39 Площина в просторі.
- •3.40. Рівняння площини в векторній і координатній формі:
- •3.53 Полряні координта точки.
- •3.54. Зв'язок між полярними і декартовими координатами.
- •3.55. Рівняння кривих в полярних координатах. Побудова кривих, що задані рівняннями в полярних координатах
- •3.56 Параметричне задання лінії
- •3.57 Параметричне рівняння кривої на площині і в просторі.
- •3.58. Побудова кривих, що задані параметричними рівняннями на площині.
- •3.60. Канонічні рівняння поверхонь іі порядку:
- •3.61. Дослідження форми цих поверхонь.
1.1Визначники.
Визначник або детермінант — одна з
найважливіших характеристик квадратних
матриць.Для квадратної матриці розміру
визначник є многочленом степеня від
елементів матриці, і є сумою добутків
елементів матриці зі всіма можливими
комбінаціями різних номерів рядків і
стовпців (в кожному із добутків є рівно
по одному елементу з кожного рядка і
кожного стовпця). . Визначником другого
порядку

називається
число
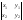 =x1y2–y1x2.Означення.
Визначником третього порядку називається
число
=x1y2–y1x2.Означення.
Визначником третього порядку називається
число
 =x1y2z3+y1z2x3+z1x2y3–z1y2x3–y1x2z3–
x1z2y3
=x1y2z3+y1z2x3+z1x2y3–z1y2x3–y1x2z3–
x1z2y3
Для обчислення визначника третього порядку існує правило трикутників. Визначник є сумою 6-и добутків, з яких три беруться зі знаком „+” і три – зі знаком „–”. Зі знаком „+” береться добуток елементів головної діагоналі і добуток елементів, які знаходяться у вершинах двох трикутників з основами, паралельними головній діагоналі
1.2 Властивості визначників Якщо помножити якийсь рядок на константу то визначник також помножиться на константу. Якщо у матриці поміняти місцями будь-які два рядки, то знак визначника зміниться на протилежний. При додаванні до будь-якого рядка лінійної комбінації кількох інших рядків визначник не зміниться. У матриці з двома однаковими рядками або з нульовим рядком, визначник дорівнює нулю. Всі властивості визначників, що стосуються рядків, так само справедливі і для стовпців. Визначник трикутної матриці дорівнює добутку елементів на діагоналі. Теорема Лапласа: визначник квадратної матриці дорівнює сумі добутків елементів деякого рядка на відповідні їм алгебраїчні доповнення.
Сума добутків елементів деякого рядка на алгебраїчні доповнення відповідних елементів паралельного рядка дорівнює нулю.
1.3 Визначник н-го порядку. Означення. Визначником n- го порядку матриці А називається алгебраїчна сума всіх можливих добутків її елементів, побудованих за правилом: з кожного рядка і кожного стовпчика в добуток береться по одному і лише по одному елементу. Якщо після упорядкування елементів в добутку за першим індексом другі індекси утворюють парну перестановку, то перед добутком ставиться знак „+”, якщо непарну, то знак „-”.
Метод зведення визначника до трикутного вигляду
Визначником трикутного вигляду відносно головної діагоналі називається визначник, всі елементи якого, що стоять вище або нижче головної діагоналі, дорівнюють нулю. Такий визначник дорівнює добутку елементів його головної діагоналі.
 =
a11a22…ann
=
a11a22…ann
Визначником трикутного вигляду відносно побічної діагоналі називається визначник, всі елементи якого, що стоять вище або нижче побічної діагоналі, дорівнюють нулю. Такий визначник складається лише з одного добутку елементів побічної діагоналі.
Метод виділення лінійних множників
Метод використовується, коли елементи визначника можна вважати многочленами від одної або кількох змінних. В цьому випадку і самий визначник є многочленом від цих змінних.
1.4 Мінор. Алгебраїчне доповнення. Мінором -го порядку матриці називається визначник матриці, утворений елементами на перетині стовпців та рядків. Визначник матриці, яка одержується з викреслюванням всіх рядків та стовпців, окрім вибраних, називається мінором n-го порядку, розташованим в рядках з номерами та стовпцях з номерами .
Алгебраїним
доповненням елемента![]() називають мінор цього елемента, взятий
зі знаком
називають мінор цього елемента, взятий
зі знаком
![]() тобто
тобто
![]() - алгебраїчне доповнення
- алгебраїчне доповнення
1.5 Матриця. Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця) і допускаючий операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В даній статті вони розглядатися не будуть. Матриці є корисними для запису даних, що залежать від двох категорій, наприклад: для коефіцієнтів систем лінійних рівнянь та лінійних перетворень.Горизонтальні лінії в матриці звуть рядками, вертикальні — стовпцями.
Матрицю, що складається з m рядків та n стовпців, називають матрицею m-на-n (або mn-матрицею), а m і n — її розмірністю.Елемент матриці A, що знаходиться на перетині i-го рядка з j-им стовпчиком, називають i,j-им елементом або (i,j)-им елементом A.
Якщо дано дві матриці m-на-n A і B, можемо означити їх суму A + B як матрицю m-на-n, що утворюється додаванням відповідних елементів, себто,
(A + B)[i, j] = A[i, j] + B[i, j]. Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, n стовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, p стовпчиків), що розраховується за формулою:
(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.
1.6 Лінійні операції над матрицями. Справедливі такі властивості операцій:
а) А - В = В + А — комутативність відносно додавання матриць;
б) А + (В + С) — (А + В)+С — асоціативність відносно додавання матриць;
в) А + О — А; А — А = О — роль нульової матриці в діях над матрицями така, як і числа нуль в діях над числами;
г) (βA) = (β) А — асоціативність відносно множення чисел;
д) (А + В) = А +В — дистрибутивність множення на число відносно додавання матриць;
е) ( + β) А — А + βА — дистрибутивність множення на матрицю відносно додавання чисел.
4°. Операція множення двох матриць вводиться лише для узгоджених матриць. Матриця А називається узгодженою з матрицею В, якщо кількість стовпців першої матриці А дорівнює кількості рядків другої матриці В.
Якщо ця умова не виконується, тобто матриці неузгоджені, то множення таких матриць неможливе.
З узгодженості матриці А з В не випливає, взагалі кажучи, узгодженість матриці В з А.
Квадратні матриці одного порядку взаємно узгоджені.
Добутком С = А В матриці Аmn — (аij) на матрицю Bnk=(bij) називається така матриця, у якої елемент сij дорівнює сумі добутків елементів j-го рядка матриці А на відповідні елементи четвертого стовпця матриці В:
cij=ai1b1j+ai2b2j+ … + ainbnj; C = Cmk = (cij),
i = 1, 2, …, m; j = 1, 2, …, k.
Це означення називають правилом множення рядка на стовпець. Наприклад, щоб визначити елемент с24, що стоїть в другому рядку і четвертому стовпці матриці С = АВ, потрібно знайти суму»добутків елементів другого рядка матриці А на відповідні елементи четвертого стовпця матриці В.
Для дій 1°—4° над матрицями виконуються такі властивості (за умови, що вказані операції мають зміст):
а) (АВ) С = А (ВС); б) (А) В = А (В) = (АВ);
в) (A + В) С = AС + BС; г) С (A + В) = СA + СB;
д) A • О = О • А = О; е) АЕ = ЕА = A; е) det (A5) = det А X det 5.
Обернена матриця
Нехай А — квадратна матриця. Матриця A-1 називається оберненою до матриці А, якщо виконується умова
А* А-1 = А-1*А = Е.
1.7
Множення матриць.
Множення двох матриць має сенс лише
тоді, коли число стовпчиків першої
матриці дорівнює числу рядків другої
матриці. Якщо A — матриця m-на-n (m рядків,
n стовпчиків), а B — матриця n-на-p (n рядків,
p стовпчиків), їх добуток AB є матрицею
m-на-p (m рядків, p стовпчиків), що
розраховується за формулою:
(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.
1.8 Поняття рангу матриці.
Рядки
цієї
матриці
можна
розглядати
як
n- вимірні
вектори
a1,
a2,…
am
з
дійсними
координатами
(елементи
простору
Rn).
Ранг
системи векторів a1,
a2,…
am
називається горизонтальним рангом
матриці
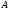 (або рангом матриці
(або рангом матриці
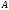 за рядками) і позначається .rr(A).
за рядками) і позначається .rr(A).
Стовпчики матриці A можна розглядати як m- вимірні вектори b1, b2,…bn
з дійсними координатами (елементи простору Rm). Ранг системи векторів b1, b2,…bn називається вертикальним рангом матриці A (або рангом матриці A за стовпчиками) і позначається rb(A).
Введемо ще одне значення рангу матриці.
Мінором матриці A порядку k (k≤m,k≤n) називається визначник, побудований на перетині будь-яких k рядків і k стовпчиків матриці.
В матриці A візьмемо всі мінори, які не дорівнюють нулю. Серед них виберемо мінор найвищого порядку. Порядок цього мінору будемо називати рангом матриці A за мінорами і позначати rm(A). Якщо всі елементи матриці дорівнюють нулю, ранг матриці за мінорами будемо вважати рівним нулю.
1.9 Обернена матриця. Означення 1. Якщо для квадратної матриці A існує така матриця X, що AX=XA=E (одинична матриця), то матрицю X називають оберненою матрицею до матриці A і позначають A−1.
Твердження 2. Обернена матриця для кожної матриці єдина.
Означення 3. Матриця, детермінант якої дорівнює нулю, називається особливою (виродженою). В іншому випадку, матриця називається неособливою (невиродженою).
Теорема 4. Щоб матриця мала обернену, необхідно і достатньо, щоб вона була неособливою.
Властивості оберненої матриці:
1. det(A−1)=(detA)−1
2. (AB)−1=B−1A−1
3. (AT)−1=(A−1)T
1.10Система лінійнихалгебраїчних рівнянь. Система лінійних алгебраїчних рівнянь (СЛАР) — в лінійній алгебрі це система лінійних рівнянь виду:

Це система m лінійних рівнянь з n невідомими, де
![]() є
невідомими
є
невідомими
![]() є
коефіцієнтами системи
є
коефіцієнтами системи
![]() є
вільними членами
є
вільними членами
Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задач лінійної алгебри, теорії диференціальних рівнянь, математичної фізики, тощо, та областей фізики й техніки, де застосовуються ці математичні теорії.
Матричний запис :
![]()
чисел x1,x2,...,xn, яка при підстановці кожне рівняння системи перетворює його в тотожність.
Якщо система має хоча б один розв’язок, то вона називається сумісною, і несумісною, якщо не має жодного. Відповідь на питання сумісності системи дає теорема Кронекера-Капеллі.
Сумісна система називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо вона має безліч розв’язків. В останньому випадку кожен її розв’язок називають частковим розв’язком системи. Сукупність усіх часткових розв’язків називають загальним розв’язком системи.
Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод Крамера — чисто теоретичний метод, непридатний до практичного використання через обчислювальну складність і малу точність, оскільки вимагає обчислення визначників, а тільки в одному визначнику n! доданків. Метод Крамера може застосовуватися для матриць 2×2, або, щонайбільше, 3×3.
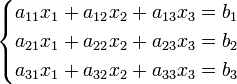
![]()
![]()
