II. Основы молекулярно-кинетической теории

1. Основное уравнение молекулярно-кинетической теории газов

где р – давление газа; n – концентрация молекул; m₀ – масса молекулы; <υ²> – средний квадрат скорости поступательного движения молекулы; ρ – плотность; <ε_к> – средняя кинетическая энергия поступательного движения молекулы.

2. Закон равномерного распределения энергии по степеням свободы: на каждую степень свободы поступательного и вращательного движения молекулы приходится средняя энергия .

3. Средняя энергия молекулы газа ,

где i – число степеней свободы молекулы.

4. Скорости молекул газа:

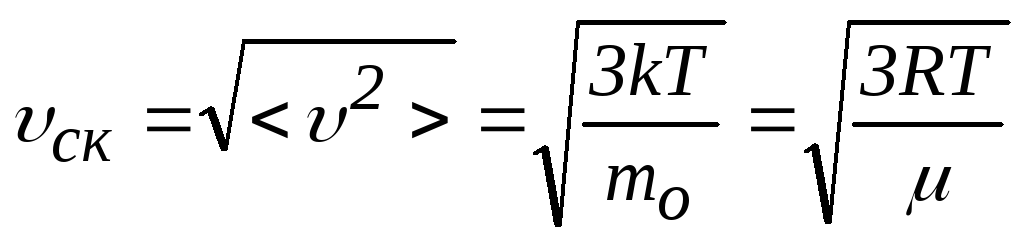– среднеквадратичная скорость;

– средняя арифметическая скорость;

– наиболее вероятная скорость.

5. Функция распределения Максвелла

.

6. Распределение Больцмана

,

где n – концентрация молекул с потенциальной энергией E_П;

n₀ – концентрация молекул с потенциальной энергией E_П=0;

E_П – потенциальная энергия молекулы.

Примеры решения задач

Задача 1. При давлении газа, равном 0,1 МПа, его двухатомные молекулы обладают средней кинетической энергией 2,5·10^-20 Дж. Определить концентрацию молекул газа.

Дано: Решение:

i = 5 Воспользуемся основным уравне-

р = 1·10⁵ Па нием молекулярно-кинетической

<ε_к>= 2,5·10^-20 Дж теории газов:

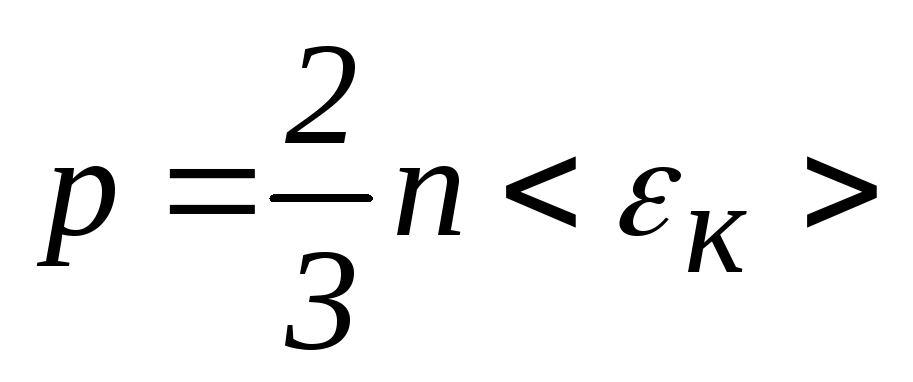. (1)

n – ? Так как средняя кинетическая энергия поступательного движения молекулы , а средняя энергия молекулы, включая кинетическую энергию вращательного движения,

,

то с учетом закона равномерного распределения энергии по степеням свободы для <ε> получаем

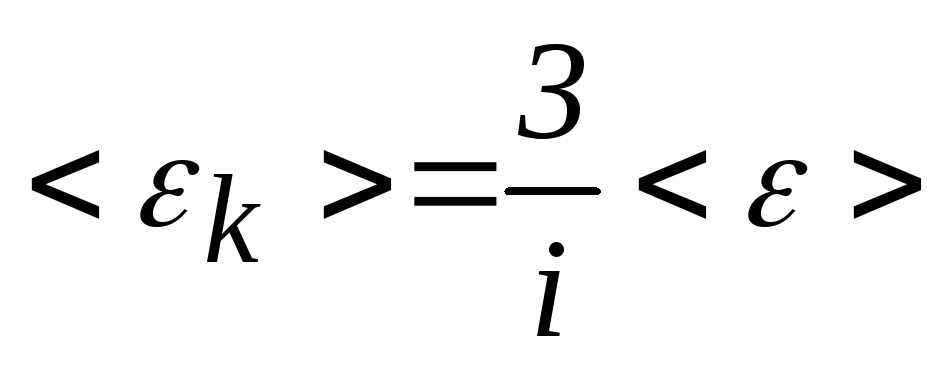. (2)

Используя формулы (1) и (2), находим

.

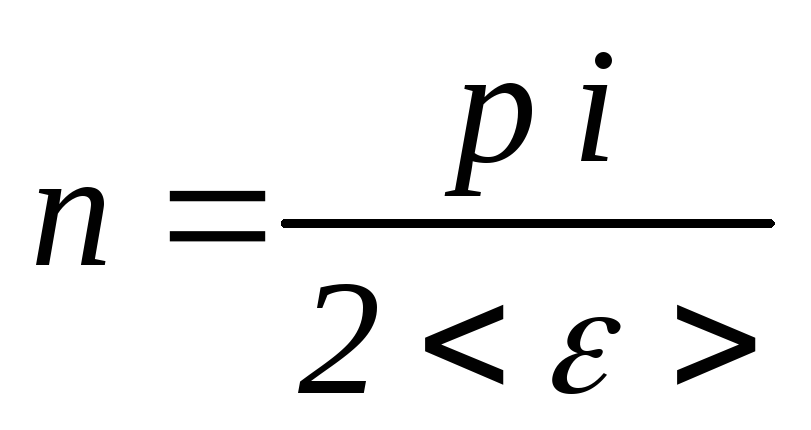Проверка размерности:

.

Вычисления:

.

Ответ: 1,0·10²⁵ м^-3.

Задача 2. Определить наиболее вероятную скорость, среднюю арифметическую скорость и среднюю квадратичную скорость молекул газа, у которого при нормальном атмосферном давлении плотность равна 0,3 кг/м³.

Дано: Решение:

р = 105 Па Для нахождения искомых скоростей

ρ = 0,3 кг/м³ воспользуемся формулами их определений.

При этом параметры (температуру и молярную массу), входящие в эти формулы, выразим из уравнения состояния идеального газа .

Таким образом, получаем

– наиболее вероятная скорость;

– средняя арифметическая скорость;

– средняя квадратичная скорость.

Проверка размерности:

.

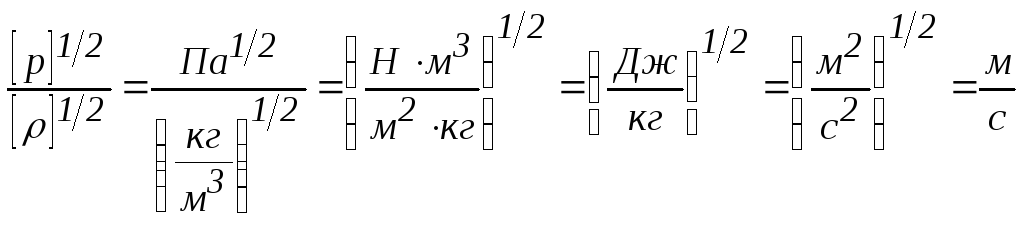Вычисления:

;

;

.

Ответ: , , .

Задача 3. Определить наиболее вероятную скорость молекул газа, находящегося в состоянии теплового равновесия, при котором значениям скоростей молекул 300 м/с и 600 м/с соответствуют одинаковые значения функции распределения Максвелла.

Дано: Решение:

υ₁ = 300 м/с Функция распределения Максвелла:

υ₂ = 600 м/с

.

Учитывая выражение для определения наиболее вероятной скорости

,

получаем функцию распределения Максвелла в следующем виде:

.

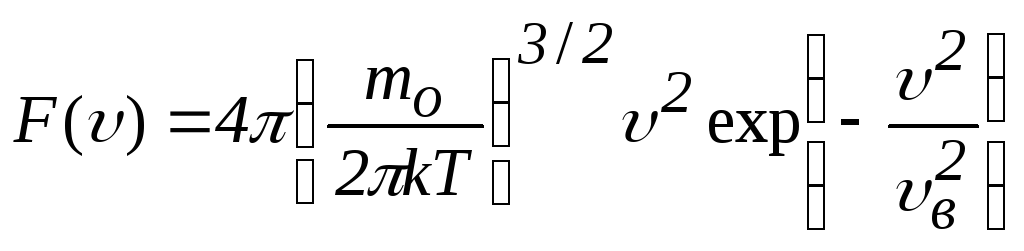Применив полученное выражение для двух значений скоростей, с учетом условия задачи получаем

.

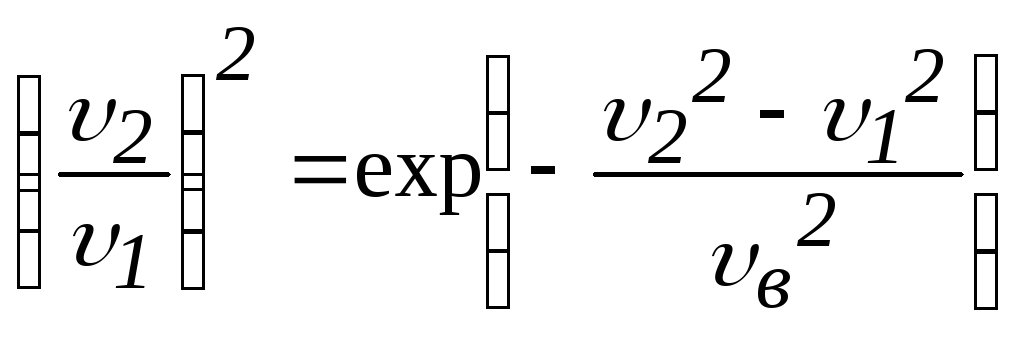Логарифмируем и выражаем искомую величину.

.

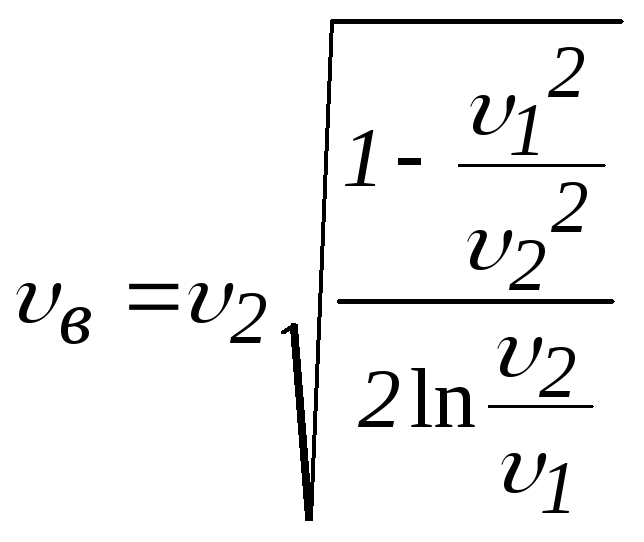Соответствие размерности очевидно.

Вычисления: .

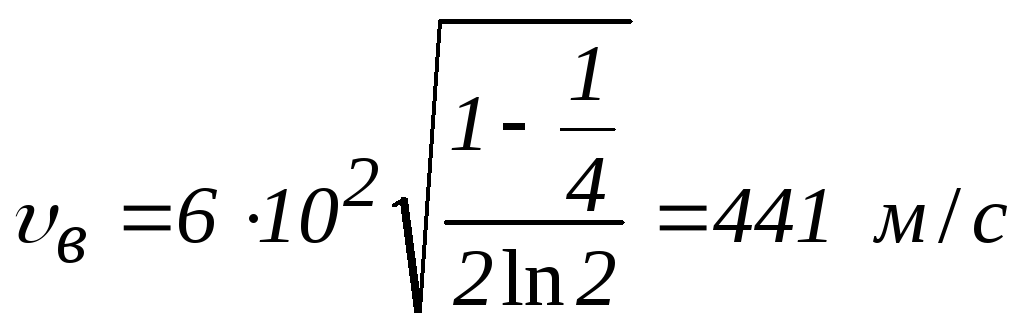Ответ: 441 м/с.

Задача 4. При наблюдении в микроскоп взвешенных в жидкости частиц гуммигута обнаружено, что концентрация частиц в одной фокальной плоскости в два раза больше их концентрации в другой фокальной плоскости, расстояние между которыми 40 мкм. Температура жидкости 17 °С. Диаметр частиц 0,4 мкм, а плотность гуммигута на 0,2 г/см³ больше плотности окружающей жидкости. Определить по этим данным число Авогадро.

Дано: Решение:

∆h = 40 мкм = 4 ·10^-5 м Распределение частиц, взвешенных

в жидкости, подчиняется закону

Т = 17 °С = 290 К Больцмана:

d = 0,4 мкм = 4·10^-7 м . (1)

Поле тяжести Земли в пределах рассматриваемых изменений высоты можно считать однородным. Если учесть, что частицы гуммигута испытывают действие выталкивающей силы Архимеда

, (2)

где V – объем частицы, то для потенциальной энергии частицы следует записать

Концентрации частиц в фокальных плоскостях на высотах h₁ и h₂, отсчитанных от дна сосуда, согласно уравнению (1), равны

,

.

Найдем отношение

. (3)

Учитывая, что , , ∆h= h₁ – h₂ , из (3) находим

.

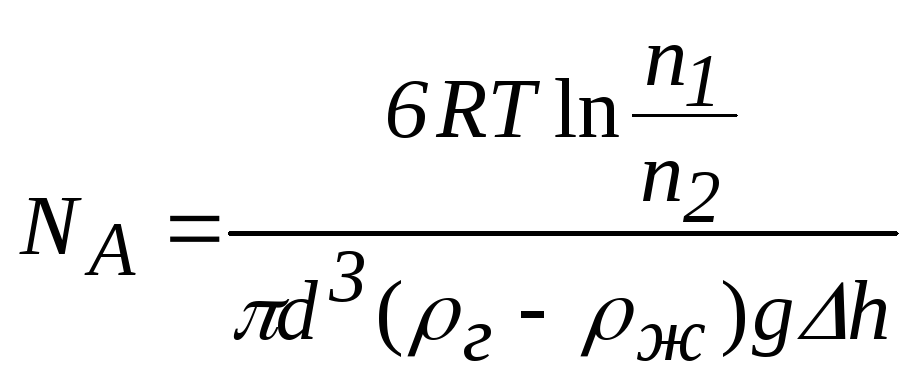Проверка размерности: .

Вычисления:

.

Ответ: 6,4·10²³ 1/моль.