Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

"Ивановский государственный энергетический

университет имени В.И. Ленина"

Кафедра физики

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Методические указания к выполнению

рассчетно-графического задания

по физике №2

Иваново 2008

Составители: В.Х. Костюк,

О.А. Кабанов,

Г.А. Шмелева

Редактор В.К. Ли-Орлов

Содержат математические формулировки основных определений и законов молекулярной физики и термодинамики с пояснениями, примеры решений типовых задач, образцы оформления решений, задания для самостоятельной работы студентов по курсу "Молекулярная физика и термодинамика". Предназначены для обеспечения самостоятельной работы студентов.

Утверждены цикловой методической комиссией инженерно-физического факультета.

Рецензент

кафедра физики ГОУВПО "Ивановский государственный энергетический университет имени В.И. Ленина"

Молекулярная физика и термодинамика

Методические указания к выполнению расчетно-графического задания по физике №2

Составители: КОСТЮК Владимир Харитонович,

КАБАНОВ Олег Альбертович,

ШМЕЛЕВА Галина Александровна

Редактор М.А. Иванова

Лицензия ИД № 05285 от 4 июля 2001 года

Подписано в печать Формат 60х84.

Печать плоская. Усл. печ. л. 2,79. Тираж 150 экз. Заказ №

ГОУВПО "Ивановский государственный энергетический университет имени В.И. Ленина"

Отпечатано в РИО ИГЭУ

153003, г. Иваново, ул. Рабфаковская, 34.

Программа курса "Молекулярная физика и термодинамика"

Термодинамические системы. Методы молекулярной физики, статистической физики и термодинамики. Термодинамические параметры. Состояния термодинамической системы. Уравнения состояния идеального газа. Термодинамические процессы. Диаграммы состояний и процессов.

Основное уравнение молекулярно-кинетической теории идеального газа. Средняя кинетическая энергия молекул. Абсолютная температура. Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул. Распределение молекул идеального газа по скоростям – распределение Максвелла. Барометрическая формула. Распределение молекул идеального газа по энергиям в потенциальном поле – распределение Больцмана.

Термодинамика идеального газа. Термодинамические функции: внутренняя энергия, работа, количество теплоты. Первый закон термодинамики. Работа в изохорном, изобарном и изотермическом процессах. Теплоемкость. Теплоемкость идеального газа. Соотношение Майера. Адиабатный процесс. Уравнение Пуассона.

Циклические процессы. Цикл Карно. Тепловая машина. КПД тепловой машины. КПД идеальной тепловой машины. Теорема Карно.

Обратимые и необратимые процессы. Второй закон термодинамики. Энтропия. Теорема Нернста. Энтропия идеального газа. Понятия порядка и беспорядка. Статистический вес. Формула Больцмана. Статистический смысл второго закона термодинамики.

Кинетические явления. Среднее число столкновений и средняя длина свободного пробега молекул. Диффузия, теплопроводность и внутреннее трение.

Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реального газа. Фазовые переходы 1-го рода. Критическое состояние вещества.

I. Уравнение состояния идеального газа процессы идеального газа

1. Уравнения состояния идеального газа (производные формы):

,

,

,

,

,

где р – давление;

n – концентрация молекул;

k = 1,38 10^-23 Дж/К; – постоянная Больцмана;

T – абсолютная температура;

V – объём;

N – число молекул;

ρ – плотность газа;

μ – молярная масса;

m – масса газа;

ν – число молей;

R = 8,31 Дж/(моль·К) – универсальная газовая постоянная.

2. Закон Дальтона:

,

где p – давление смеси газов, p_i – парциальное давление i – го компонента смеси газов.

3. Термодинамические процессы в идеальном газе постоянной массы:

а) изотермический, Т = const, ;

б) изобарный, p= const, ;

в) изохорный, V = const, .

Примеры решения задач

Задача 1. В баллоне объёмом 20 л находится аргон под давлением 1,0 МПа и температуре 300 К. После того как из баллона было взято 20,0 г аргона, температура в баллоне понизилась до 280 К. Определить давление газа, оставшегося в баллоне.

Дано: Решение:

V = 20 л = 2,0·10^-2 м³ Для решения задачи воспользуемся

р₁ = 1,0 МПа = 1,0·10⁶ Па уравнением состояния идеального

Т₁ = 300 К газа, применив его к начальному и

Т₂ = 280 К конечному состояниям газа:

Δm = 20,0 г = 2,0·10^-2 кг , (1)

р₂ – ? . (2)

Из уравнений (1) и (2) выразим m₁ и m₂ и найдём их разность:

,

откуда находим

. (3)

Проверку решения проведем по размерности физических величин. В правую часть вместо символов величин подставим их единицы измерения. В правой части два слагаемых. Первое из них имеет размерность давления, так как состоит из двух множителей, первый из которых – давление, а второй – безразмерный. Проверим второе слагаемое:

.

Вычисления произведём по формуле (3) с учётом, что для аргона кг/моль.

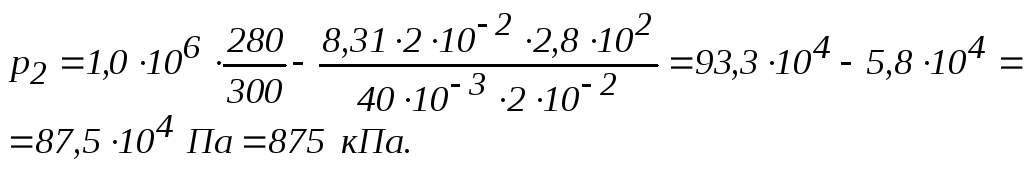Ответ: 875 кПа.

Задача 2. В сосуде находится смесь 14,0 г азота и 16,0 г кислорода при температуре 300 К и давлении 8,3 кПа. Определить плотность этой смеси, считая газы идеальными.

Дано: Решение:

Для каждого компонента в смеси

газов можно записать уравнения

состояния:

, (1)

. (2)

Давление смеси равно (по закону Дальтона). Суммируя (1) и (2), с учётом закона Дальтона найдём объём газа

.

Для плотности смеси находим

.

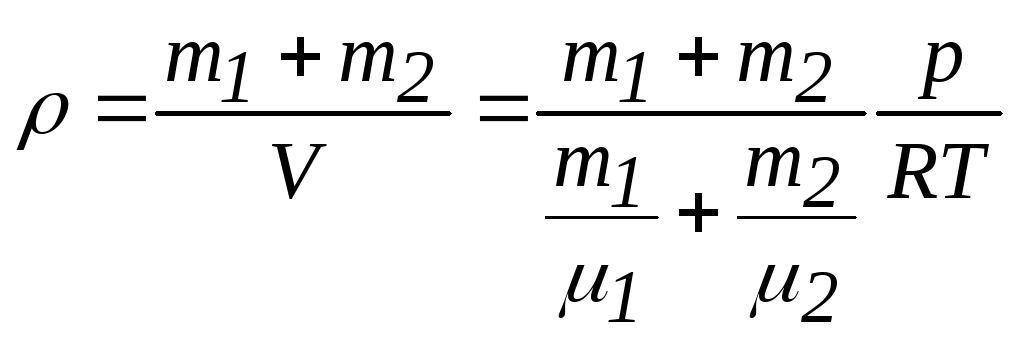Проверка размерности:

.

Вычисления:

.

Ответ: 0,1 кг/м³.

Задача 3. Поршневым воздушным насосом откачивают баллон объёмом 10,0 л. За один цикл (ход поршня) насос захватывает объём 0,4 л. Через сколько циклов давление в баллоне уменьшится от 0,1 МПа до 0,1 кПа? Процесс считать изотермическим, газ – идеальным.

Дано: Решение:

V = 10 л = 1,0 10^-2 м³ Для изотермического процесса в первом

ΔV = 0,4 л = 0,4 10^-3 м³ и следующих циклах можно записать

р₀ = 0,1 МПа = 1,0 10⁵ Па ,

р_N = 0,1 кПа = 100 Па ,

Т = const -----------------------

N – ? .

Получаем рекуррентную формулу

, (1)

где N – число циклов. Прологарифмировав соотношение (1), получим для числа циклов

. (2)

Правая часть (2) содержит отношения однородных величин и является безмерной.

Вычисления:

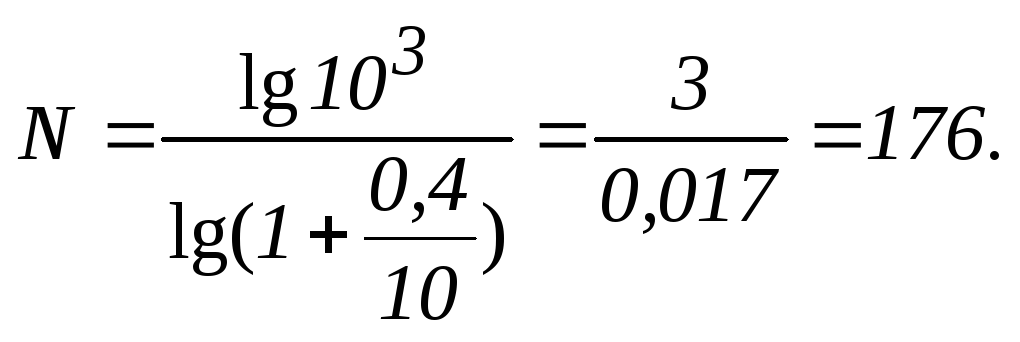
Ответ: 176 циклов.

Задача 4. Идеальный газ совершает процесс, в котором давление изменяется в зависимости от объёма по закону p=p₀–αV², где p₀=0,1 МПа, α=1,0·10⁷ Па·моль²/м⁶. Количество вещества газа равно 1 моль. Определить максимальную температуру газа в процессе.

Дано: Решение:

р = р₀ – αV² Найдём зависимость . Для этого

р₀= 0,1 МПа = 10⁵ Па воспользуемся уравнением состояния для

α = 1,0·10⁷ Па·моль²/м⁶ одного моля газа

Т_max – ? .

Исключая давление, получим

. (1)

Из условий

находим максимум функции T(V). Получается, что в области положительных значений V и Т зависимость (1) при объёме моля газа

имеет максимальную температуру, равную

.

Проверка размерности:

.

Вычисления:

.

Ответ: 465 К.