5. Перемещения поперечных сечений брусьев при растяжении и их эпюры

При растяжении (сжатии) бруса его поперечные сечения перемещаются в направлении оси. Перемещения являются следствием деформаций, но эти понятия необходимо строго разграничивать.

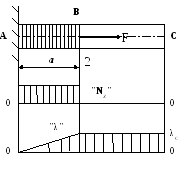
Например, в случае, представленном на рисунке, деформируется лишь левая часть бруса (участок АВ), а участок ВС перемещается как абсолютно твёрдое тело. Перемещения всех сечений этого участка одинаковы и равны удлинению части АВ бруса.

Перемещение произвольного сечения бруса равно изменению длины участка, заключённого между этим сечением и заделкой (на расстоянии z).

График, показывающий перемещения поперечных сечений в функции их расстояния z от жёстко защемлённого конца бруса, называется эпюрой перемещений.

Взаимное перемещение двух сечений равно изменению длины части бруса, заключённой между этими сечениями.

6. Общие сведения о механических испытаниях материалов

Выбирая материал для проектируемой детали, а затем рассчитывая её на прочность, жёсткость и устойчивость, конструктор должен располагать данными о механических свойствах материала.

Основные механические характеристики, определяемые при испытаниях материалов:

Прочность – это способность материала конструкций выдерживать определенную нагрузку без разрушения.

Пластичность – способность материала давать остаточные деформации без разрушения.

Упругость – способность материала восстанавливать первоначальную форму и размеры после снятия нагрузки.

Твёрдость – способность материала сопротивляться проникновению в него другого материала, практически недеформируемого.

Классификация видов испытаний:

По характеру нагружения:

- статические;

- динамические;

- повторно-переменные (испытания на выносливость).

По виду деформации:

- испытания на растяжение, сжатие, изгиб, кручение, срез;

- испытания в условиях сложного напряжённого состояния.

Испытание материалов на растяжение

При испытании на растяжение нагрузка к образцам прикладывается статически, т.е. медленно, плавно, с постепенным непрерывным нарастанием.

Для того, чтобы результаты испытаний, проведённых различными лабораториями, были сопоставимы, используются стандартные типы и размеры образцов.

Образец закрепляют концами в захваты разрывной машины. Затем растягивают плавно возрастающей нагрузкой. В процессе испытания самопишущее автоматическое устройство машины вычерчивает диаграмму растяжения, на которой по оси ординат отмечается величина нагрузки, а по оси абсцисс – величина абсолютных удлинений. Эта диаграмма зависит не только от свойств материала, но и от размеров испытуемого образца. Чтобы получить диаграмму, характеризующую только механические свойства материала, перестраивают диаграмму в координатах σ – ε . Эти две диаграммы отличаются друг от друга лишь масштабами.

где А₀ и l₀ – первоначальная площадь поперечного сечения образца и первоначальная длина.

На рисунке представлена диаграмма растяжения низкоуглеродистой стали.

В начальный момент σ₀=0, ε₀ =0. При увеличении нагрузки стержень получает удлинение, которое растёт пропорционально силе. Прямая ОА графически выражает закон Гука. В образце возникают упругие деформации.

Диаграмма имеет следующие характерные точки.

Точка А соответствует пределу пропорциональности.

Предел пропорциональности (σ_pr) ─ это наибольшее напряжение, до которого деформации растут пропорционально нагрузке, т.е. справедлив закон Гука.

Тангенс угла наклона α прямого участка ОА к оси абсцисс равен модулю упругости Е.

Выше точки А диаграмма представляет собой кривую линию, деформации растут быстрее роста напряжений. В образце наряду с упругими возникают и небольшие остаточные деформации, которые настолько малы (меньше 0,05%), что ими пренебрегают. Точка А практически соответствует и пределу упругости.

Предел упругости (σ_el) ─ это наибольшее напряжение, до которого в образце не возникают остаточные деформации.

Начиная с точки С диаграмма имеет горизонтальный участок, показывающий, что деформации растут даже без увеличения нагрузки – площадка текучести. Точка С соответствует пределу текучести.

Предел текучести (σ_у) ─ это напряжение, при котором происходит рост пластических деформаций при практически постоянной нагрузке.

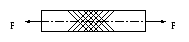
При достижении предела текучести повышается температура образца; поверхность его становится матовой, так как на ней появляется сетка линий Людерса-Чернова, наклонённых под углом 45⁰ к оси стержня. Эти линии представляют собой следы максимальных сдвигов частиц материала, соответствующие наибольшим касательным напряжениям τ_max. В результате этих сдвигов образец получает пластические деформации.

Предел прочности (σ_u) ─ это условное напряжение, соответствующее наибольшей нагрузке, выдерживаемой образцом до разрушения.

Пластичность материала характеризуются относительным остаточным удлинением:

Относительное остаточное поперечное сужение:

При повторном нагружении за предел текучести предел пропорциональности увеличивается, а пластичность уменьшается. Это явление называется наклёп.

В сопротивлении материалов различают 3 группы напряжений:

1. Предельные (опасные) напряжения, σ_dan ─ напряжения, при достижении которых возникают признаки разрушения материала или остаточные деформации.

Данные напряжения зависят только от материала и вида деформации и определяются по диаграммам испытания, либо по справочным таблицам.

В качестве предельных напряжений для трёх групп материалов применяют:

- для пластичных - физический предел текучести σ_у или условный предел текучести σ_0,2.

- для хрупкопластичных - условный предел текучести σ_0,2.

- для хрупких - предел прочности σ_u.

2. Допускаемые напряжения, σ_adm ─ наибольшие напряжения, которые можно допустить в рассчитываемой конструкции, исходя из условий её безопасности, надёжности, долговечности. Зависят от свойств материала, вида деформации и требуемого коэффициента запаса прочности.

3. Расчётные (фактические) напряжения, σ_mах ─ напряжения, возникающие в рассчитываемой конструкции при заданной нагрузке. Зависят от действующих на элемент конструкции нагрузок и его размеров. Зависят от свойств материала, вида деформации и требуемого коэффициента запаса прочности.

Способы оценки прочности конструкции:

1. Условие прочности по коэффициенту безопасности.

В этом случае определяют расчётный коэффициент запаса прочности и сравнивают его с заданным или требуемым.

Расчётный коэффициент запаса прочности (S) равен отношению предельного напряжения к расчётному напряжению (его величина всегда должна быть больше 1).

Условие прочности

где S_adm - заданный или требуемый коэффициент запаса прочности, или коэффициент безопасности (минимально необходимый), нормативный.