2. Нормальные напряжения при растяжении (сжатии)

При растяжении и сжатии бруса в его поперечных сечениях возникают только нормальные напряжения σ. Для их определения при известной продольной силе, необходимо установить закон их распределения по поперечному сечению бруса.

Эта задача решается на основе гипотезы Бернулли: перпендикулярное оси недеформированного бруса плоское сечение остаётся таким же плоским и перпендикулярным оси и при растяжении (сжатии) бруса.

При растяжении бруса, изготовленного для большей наглядности опыта из резины, на поверхности которого нанесена система продольных и поперечных рисок, можно убедиться, что риски остаются прямолинейными и взаимно перпендикулярными, изменяются лишь расстояния: между поперечными – увеличиваются, а между продольными – уменьшаются. При этом предполагают, что внутри бруса деформации имеют тот же характер, что и на его поверхности.

Брус состоит из бесконечно большого числа продольных элементов, имеющих бесконечно малые поперечные сечения, – волокон.

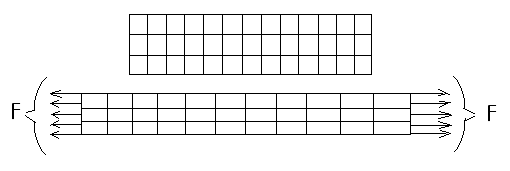
Их данной гипотезы следует, что все волокна деформируются одинаково. При однородном материале равным деформациям соответствуют одинаковые напряжения.

Следовательно, при растяжении и сжатии бруса нормальные напряжения распределены по его поперечному сечению равномерно.

где А – площадь поперечного сечения, которая является геометрической характеристикой прочности бруса при растяжении и сжатии.

Для нормальных напряжений принимают тоже правило знаков, что и для продольных сил.

График, показывающий закон изменения нормальных напряжений по всей длине бруса, называется эпюрой нормальных напряжений.

3. Деформации при растяжении и сжатии

При растяжении бруса его первоначальная длина l увеличивается на Δl (абсолютное удлинение), а первоначальный поперечный размер d уменьшается на Δd (абсолютное поперечное укорочение); при сжатии – наоборот.

При растяжении Δ l >0, Δ d <0.

При сжатии Δ l <0; Δ d >0.

Величина абсолютного удлинения или укорочения, зависящая от длины бруса, не даёт общего представления о значительности деформации.

Деформирование бруса при растяжении и сжатии характеризуют величины:

Относительное удлинение (продольная деформация) – отношение величины абсолютного удлинения к первоначальной длине бруса

Относительное поперечное сужение (расширение) (поперечная деформация) – отношение изменения поперечного размера к его первоначальному значению

Продольная и поперечная деформации пропорциональны друг другу, что выражает коэффициент Пуассона, характеризующий упругие свойства материала

ν=0…0,5. Для пробки ν=0; для стали ν=0,25…0,33; для парафина ν=0,5.

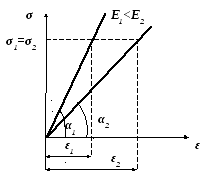
4. Закон Гука: В пределах упругих деформаций между нормальными напряжениями и продольной деформацией существует прямо пропорциональная зависимость:

где Е – модуль продольной упругости (модуль Юнга) – это физическая постоянная данного материала, характеризующая его жёсткость.

Чем жёстче материал, тем меньше он деформируется при данном напряжении.

Для стали Е=(1,9…2,15)10⁵МПа.

Определим изменение длины бруса.

Изменение длины бруса равно алгебраической сумме удлинений (укорочений) его отдельных участков и вычисляется по формуле Гука: абсолютное удлинение прямо пропорционально продольной силе, длине и обратно пропорционально жёсткости сечения бруса

где N_i, l_i, А_i – соответственно продольная сила, длина и площадь сечения в пределах каждого участка бруса;

Произведение АЕ – условно называется жёсткостью сечения бруса при растяжении и сжатии.