Напряжения

Внутренние силы распределены по сечению непрерывно, при этом их значения в разных точках сечения в общем случае неодинаковы. Для суждения об интенсивности внутренних сил в определенной точке сечения вводят понятие о напряжении.

Выделим в окрестности интересующей нас точки сечения малую площадку площадью ΔА; допустим, что на этой площадке возникает внутренняя сила ΔR.

Отношение этой внутренней силы к площади выделенной площадки называется средним напряжением.

Чем точнее нужно знать интенсивность внутренних сил в данной точке сечения, тем меньше должна быть выделенная площадка.

Истинное напряжение в данной точке получим перейдя к пределу при стремлении ΔА к нулю.

(единицы измерения 1МПа=1Н/мм²=10⁶Па)

Истинное напряжение р складывается из двух составляющих:

- нормальное – σ

- касательное - τ

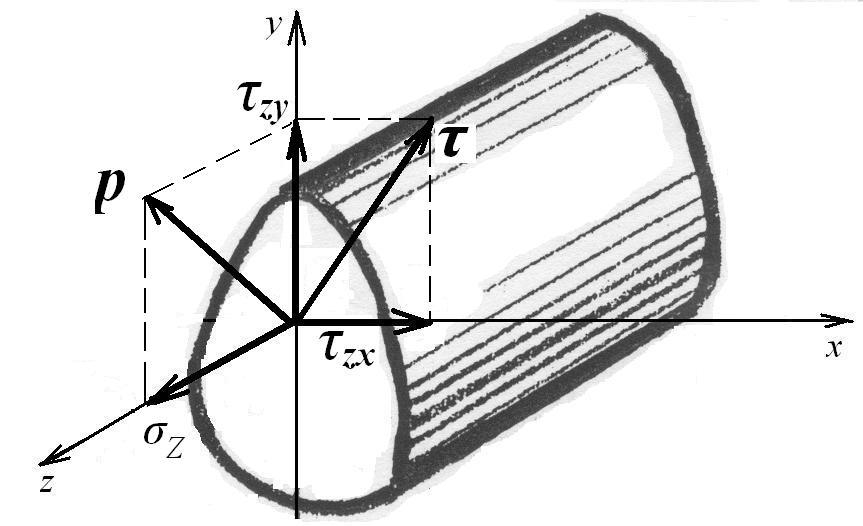
Касательное напряжение можно разложить на две составляющие, направленные вдоль осей X и Y.

2.2. Растяжение и сжатие

1. Продольные силы и их эпюры

Растяжением или сжатием называется вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – продольная сила Nz.

Прямой брус, работающий на растяжение (сжатие), называется стержнем.

Брус растянут, если внешние силы F, приложенные к его концам, действуют вдоль оси бруса и направлены в стороны от бруса; брус сжат, если силы F направлены в стороны от бруса; брус сжат, если силы F направлены к брусу.

Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси, которого действуют активные силы F и 2F.

Части бруса, заключенные между поперечными плоскостями, в которых приложены активные силы, или реактивные силы, называют участками.

Продольная сила Nz в произвольном поперечном сечении определяется с помощью метода сечений: она численно равна алгебраической сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону от сечения.

Правило знаков для Nz: при растяжении продольная сила положительна, при сжатии – отрицательна (проекции внешних сил, направленных от сечения, положительны и, наоборот, проекции внешних сил, направленных к сечению, отрицательны).

Это правило справедливо для любой оставленной части бруса.

Рассечем брус на правом участке сечением 1-1. Для уравновешивания силы 2F достаточно в сечении приложить продольную силу N_Z1, направив ее по оси.

ΣF_iz = 0; 2F – N₁ = 0

N₁ = 2F

Рассечем брус на левом участке сечением 2-2.

ΣF_iz = 0; 2F – F – N₂ = 0

N₂ = 2F – F = F

Таким образом, направление N_Z противоположно направлению проекции на ось Z равнодействующей внешних сил, приложенных к оставленной части бруса.

Если в результате сложения проекций внешних сил получилось, что N_Z>0, то продольная сила направлена от сечения и брус в этом сечении испытывает растяжение; при N_Z<0 продольная сила направлена к сечению и брус испытывает сжатие.

График, показывающий изменение продольной силы по длине бруса называют эпюрой продольных сил.

Эпюру продольных сил строят для того, чтобы использовать ее при расчете бруса на прочность; она даёт возможность найти наибольшие значения продольных сил и положение сечений, в которых они возникают.