2. Формула Эйлера для определения критической силы
где Е – модуль Юнга (характеризует жёсткость материала);
Imin – минимальный из осевых моментов инерции сечения, так как изгиб стержня происходит в плоскости наименьшей жёсткости, то есть каждое поперечное сечение стержня поворачивается вокруг той из главных осей, относительно которой момент инерции минимален;
lприв – приведенная длина стержня;
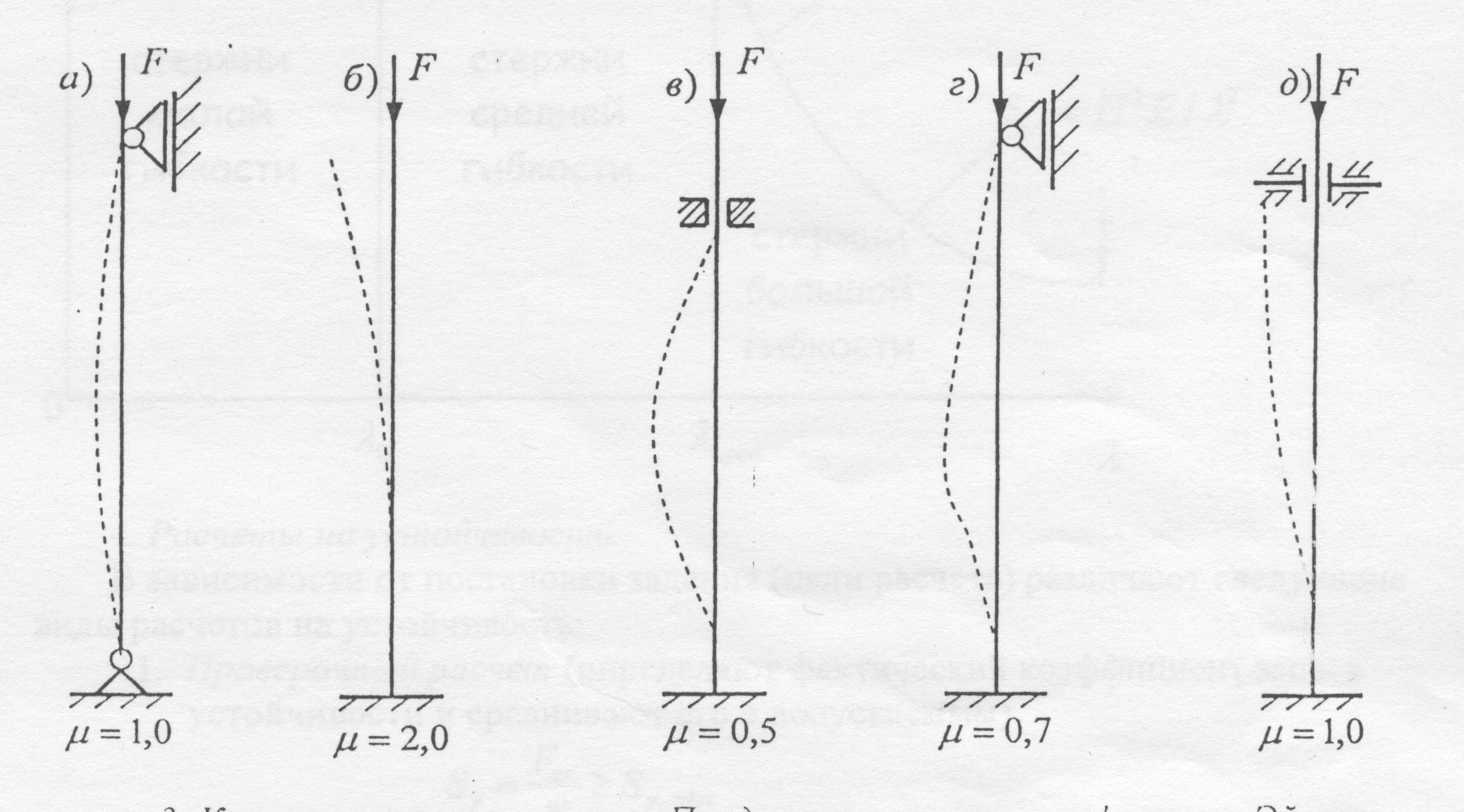
μ – коэффициент приведения длины, зависящей от способа закрепления концов стержня;
l – длина стержня;
3. Критическое напряжение. Пределы применимости формулы Эйлера
Вывод формулы Эйлера основан на законе Гука, который справедлив только до тех пор, пока напряжение превосходит пределы пропорциональности. Поэтому формулой Эйлера можно пользоваться не всегда. Для определения пределов применимости формулы Эйлера определяют критическое напряжение.
Критическое напряжение – нормальное напряжение в поперечном сечении сжатого стержня, соответствующее критической силе:
Если ввести понятие наименьшего радиуса инерции поперечного сечения стержня
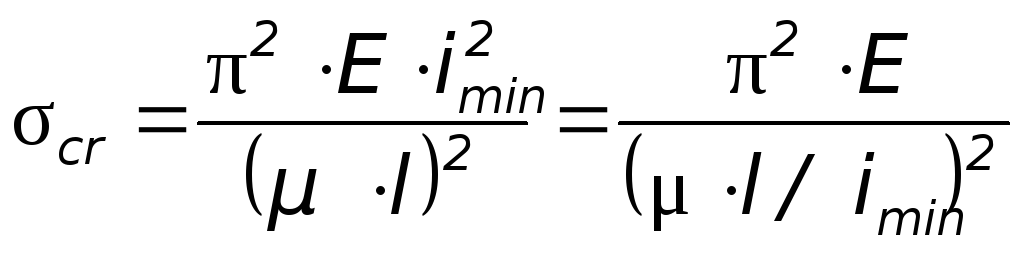
Выражение
называется гибкостью
стержня.
Это безразмерная геометрическая
характеристика сжатого стержня,
показывающая его сопротивляемость
потере устойчивости. Гибкость зависит
от длины стержня, его размеров и способа
закрепления концов стержня.
Окончательно
Условие применимости формулы Эйлера:
λпред – предельная гибкость, зависит только от физико-механических свойств материала и не зависит от его размеров и способов крепления концов стержня.
Также условие применимости формулы Эйлера можно записать в виде:
Пример: Для стали 45 (Е=2·105 МПа; σcr = 270МПа) – λпред = 85; для стали Ст3 (Е=2·105 МПа; σcr = 200МПа) – λпред = 100.
В случае неприменимости формулы Эйлера критическое напряжение определяется по эмпирической формуле Ясинского:
где а и b – коэффициенты, зависящие от материала и определяемые по таблицам справочников, МПа.
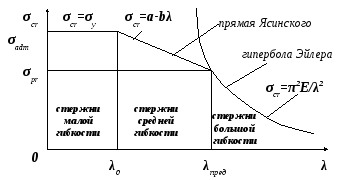
В зависимости от гибкости сжатые стержни условно делят на три категории:
1. Стержни
большой гибкости
(
).
Для них расчёт на устойчивость ведётся по формуле Эйлера (зависимость σcr от λ - гипербола Эйлера).
2. Стержни
средней гибкости
(
).
Расчёт на устойчивость ведётся по формуле Ясинского (зависимость σcr от λ - прямая Ясинского).
3. Стержни
малой гибкости
(
).
Расчёт на простое сжатие (критическое напряжение считается постоянным: σcr=σ0,2 , или σcr=σu).
4. Расчёты на устойчивость
В зависимости от постановки задачи (цели расчёта) различают следующие виды расчётов на устойчивость:
1. Проверочный расчёт (определяют фактический коэффициент запаса устойчивости и сравнивают его с допускаемым).
где F - действующая сжимающая сила.
2. Определение допускаемой нагрузки.
3. Проектный расчёт (определение требуемых размеров поперечного сечения стержня).
Расчёт сжатых стержней на устойчивость можно свести по форме к расчёту на простое сжатие. При расчёте конструкций часто применяют формулу
где σc, adm – допускаемое напряжение на сжатие;
φ – коэффициент продольного изгиба (зависит от гибкости, материала стержня, определяется по справочным таблицам).