
- •Оглавление
- •Числовые выражения Свойства дробей
- •Основное свойство дроби
- •Действия с дробями
- •Линейные уравнения и системы линейных уравнений
- •Линейное уравнение с одной переменной
- •Системы линейных уравнений
- •Алгебраические выражения
- •Формулы сокращённого умножения
- •Тождественные преобразования рациональных выражений
- •Задания для решения
- •Квадратное уравнение и его корни
- •Задания для решения
- •Теорема Виета
- •Задания для решения
- •3.5. Уравнения, сводящиеся к квадратным
- •Задания для решения
- •Множества
- •4.1 Числовые множества
- •4.2 Операции над множествами
- •Пересечение множеств
- •Объединение множеств
- •Разность множеств
- •Задания для решения
- •Прямоугольная система координат
- •Прямоугольные координаты точки
- •Функции
- •6.1. Основные понятия
- •6.2. Функции
- •Задания для решения
- •6.3 Линейная функция
- •Задания для решения
- •6.4. Функции , ,
- •Задания для решения
- •6.5. График и свойства квадратичной функции
- •Задания для решения
- •6.6. Системы уравнений с двумя переменными
- •7. Показательная и логарифмическая функции
- •7.1 Показательная функция
- •Задания для решения
- •7.2 Показательные уравнения
- •7.3.Логарифмическая функция ,
- •Задания для решения
- •7.4. Показательные и логарифмические уравнения
- •Задания для решения
- •Геометрические фигуры на плоскости
- •Треугольники
- •Задания для решения
- •Четырёхугольники
- •Задания для решения
- •Окружность и круг
- •Задания для решения
- •9. Элементы тригонометрии
- •9.1 Таблица значений тригонометрических и обратных тригонометрических функций
- •9.2 Графики тригонометрических функций
- •Задания для решения
- •9.3 Тригонометрические преобразования и уравнения
- •Задания для решения
- •Арифметическая и геометрическая прогрессии
- •10.1 Арифметическая прогрессия
- •10.2 Геометрическая прогрессия
- •Варианты заданий
Задания для решения
-
Постройте графики функций методом преобразований или с помощью таблицы значений:
|
1)
|
|
2)
|
|
3)
|
|
4)
|
7.2 Показательные уравнения
Свойства функции
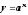 ,
,
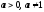
|
|
|
|
|
|
Пример 2. Решим показательные уравнения:
|
|
|
7.3.Логарифмическая функция ,
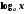 логарифм x по
основанию а.
логарифм x по
основанию а.
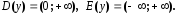
Логарифм существует только для положительных чисел.
 десятичный логарифм x.
десятичный логарифм x.
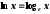 натуральный логарифм x
натуральный логарифм x
Пример 2. Построим графики функций
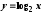 и
и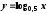 по точкам. Зададим таблицы значений:
по точкам. Зададим таблицы значений:
|
x |
0,125 |
0,25 |
0,5 |
1 |
2 |
4 |
|
|
–3 |
–2 |
–1 |
0 |
1 |
2 |
|
x |
0,125 |
0,25 |
0,5 |
1 |
2 |
4 |
|
|
3 |
2 |
1 |
0 |
–1 |
–2 |
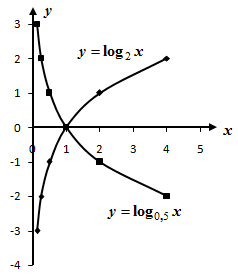
Рисунок 15.2
Функция
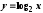 возрастает, функция
возрастает, функция
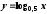 ….
….
Функция
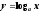 пересекает ось Ox
в точке (1;0).
пересекает ось Ox
в точке (1;0).
Задания для решения
-
Постройте графики функций:
а)
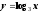 ;
;б)
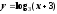 ;
;б)
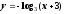 ;
;в)
 .
.
-
Постройте графики функций
а)
 ,
б)
,
б)
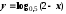 ,
в)
,
в)
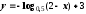 .
.
Чем отличаются эти графики?
7.4. Показательные и логарифмические уравнения
Свойства функции
 ,
,
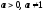
|
|
|
|
|
|
Свойства функции
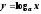 ,
,
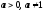
-
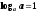 ;
; -
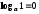 логарифм
единицы равен нулю;
логарифм
единицы равен нулю; -
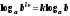 степень выносим из-под знака множителем;
степень выносим из-под знака множителем; -
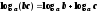 логарифм произведения равен сумме
логарифмов;
логарифм произведения равен сумме
логарифмов; -
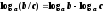 логарифм частного равен разности
логарифмов.
логарифм частного равен разности
логарифмов. -
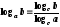 ;
; -
 ;
;
Пример 4. Решим логарифмические уравнения:
|
|
|
|
Задания для решения
-
Решите показательные уравнения:
а)
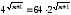 . Отв.:
35.
. Отв.:
35.
б)
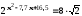 . Отв.:
5,2 и 2,5.
. Отв.:
5,2 и 2,5.
в)
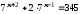 . Отв.:
1.
. Отв.:
1.
г)
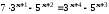 . Отв.:
– 1.
. Отв.:
– 1.
д)
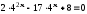 . Отв.:
. Отв.:
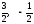 .
.
е)
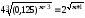 . Отв.:
3.
. Отв.:
3.
-
Решите логарифмические уравнения:
а)
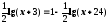 .
Отв.: 1
.
Отв.: 1
б)
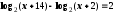 . Отв.:
2.
. Отв.:
2.
в)
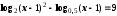 . Отв.:
9.
. Отв.:
9.
г)
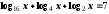 . Отв.:
16.
. Отв.:
16.
-
Геометрические фигуры на плоскости
-
Треугольники
-
|
|
|
|
|
O – точка пересечения биссектрис
Площадь треугольника:
|
Задания для решения
-
Разность двух смежных углов равна 200. Найдите больший угол.
-
Углы треугольника пропорциональны числам 3:7:8. Найдите больший угол.
-
Угол при вершине равнобедренного треугольника на 600 больше угла при основании. Найдите угол при основании треугольника.
-
В равнобедренном треугольнике угол, смежный с углом при вершине треугольника, равен 700. Найдите угол при основании треугольника.
-
Гипотенуза прямоугольного треугольника равна 26 см, а его катеты относятся как 5:12. Найдите больший катет треугольника.
-
Найдите площадь прямоугольного треугольника, если его катеты относятся как 3:4, а гипотенуза равна 25 см.
-
Один из катетов прямоугольного треугольника равен 6. Другой катет равен 8. Найдите длину медианы, проведённой к гипотенузе.
-
Катеты прямоугольного треугольника равны 6 и 8. Найдите длину медианы, проведённой к гипотенузе.
-
В прямоугольном треугольнике медиана, опущенная из прямого угла, равна одному из катетов. Найдите меньший угол треугольника.
-
В прямоугольном треугольнике острые углы относятся как 1:2. Больший катет равен
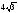 .
Найдите радиус описанной окружности.
.
Найдите радиус описанной окружности. -
В прямоугольном треугольнике АВС известно, что
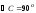 ,
,
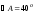 .
Около треугольника описана окружность
с центром О. Найдите угол
.
Около треугольника описана окружность
с центром О. Найдите угол
 .
. -
Катет и гипотенуза в прямоугольном треугольнике равны соответственно 10 и 26. Найдите радиус вписанной окружности.
-
Найдите радиус круга, описанного около равностороннего треугольника со стороной
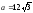 .
. -
Найдите площадь правильного треугольника со стороной
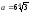 .
. -
В равностороннем треугольнике высота равна 9. найдите радиус вписанной в треугольник окружности.
-
Из вершины прямого угла С прямоугольного треугольника к гипотенузе проведены медиана СМ и высота СК. Найдите длину отрезка МК, если катеты равны 6 и
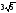 .
. -
В прямоугольный треугольник с катетами 3 и 5 вписан квадрат, имеющий с треугольником общий прямой угол. найдите периметр квадрата.
Ответы: 1. 100 . 2. 80 . 3. 40 . 4. 35 . 5. 24 см. 6. 150. 7. 5. 8. 5. 9. 30 . 10. 4. 11. 100 . 12. 4.13. 12. 14. 27. 15. 3. 16. 0,5. 17. 7,5.

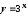 ,
,
 ;
и
;
и
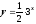 .
.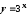 ,
,
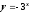 ,
,
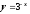 ;
и
;
и
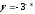 ;
;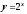 ,
,
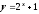 и
и
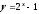 ,
,
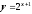 и
и
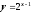 ;
;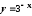 ,
,
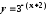 ,
,
 .
. ;
;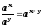 ;
;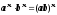 ;
; ;
; .
.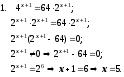
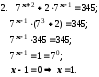
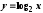
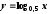
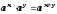 ;
;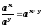 ;
;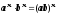 ;
;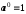 ;
;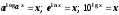 .
.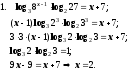
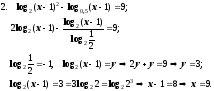
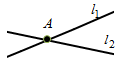
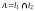 – точка пересечения прямых
– точка пересечения прямых
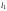 и
и
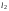

 – радиус вписанной окружности
– радиус вписанной окружности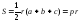
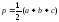 – полупериметр треугольника
– полупериметр треугольника