- •Оглавление
- •Числовые выражения Свойства дробей
- •Основное свойство дроби
- •Действия с дробями
- •Линейные уравнения и системы линейных уравнений
- •Линейное уравнение с одной переменной
- •Системы линейных уравнений
- •Алгебраические выражения
- •Формулы сокращённого умножения
- •Тождественные преобразования рациональных выражений
- •Задания для решения
- •Квадратное уравнение и его корни
- •Задания для решения
- •Теорема Виета
- •Задания для решения
- •3.5. Уравнения, сводящиеся к квадратным
- •Задания для решения
- •Множества
- •4.1 Числовые множества
- •4.2 Операции над множествами
- •Пересечение множеств
- •Объединение множеств
- •Разность множеств
- •Задания для решения
- •Прямоугольная система координат
- •Прямоугольные координаты точки
- •Функции
- •6.1. Основные понятия
- •6.2. Функции
- •Задания для решения
- •6.3 Линейная функция
- •Задания для решения
- •6.4. Функции , ,
- •Задания для решения
- •6.5. График и свойства квадратичной функции
- •Задания для решения
- •6.6. Системы уравнений с двумя переменными
- •7. Показательная и логарифмическая функции
- •7.1 Показательная функция
- •Задания для решения
- •7.2 Показательные уравнения
- •7.3.Логарифмическая функция ,
- •Задания для решения
- •7.4. Показательные и логарифмические уравнения
- •Задания для решения
- •Геометрические фигуры на плоскости
- •Треугольники
- •Задания для решения
- •Четырёхугольники
- •Задания для решения
- •Окружность и круг
- •Задания для решения
- •9. Элементы тригонометрии
- •9.1 Таблица значений тригонометрических и обратных тригонометрических функций
- •9.2 Графики тригонометрических функций
- •Задания для решения
- •9.3 Тригонометрические преобразования и уравнения
- •Задания для решения
- •Арифметическая и геометрическая прогрессии
- •10.1 Арифметическая прогрессия
- •10.2 Геометрическая прогрессия
- •Варианты заданий
Задания для решения
-
Постройте в одной системе координат графики функций
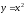 ,
,
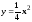 и
и
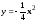 .
.
Найдите промежутки возрастания и убывания для каждой из функций.
-
Постройте в одной системе координат графики функций:

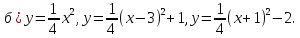
В какой точке находится вершина параболы? В какой точке парабола пересекает ось Oy?
-
Постройте график функции:
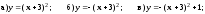
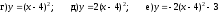 .
.
6.5. График и свойства квадратичной функции
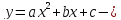
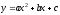 – квадратичная функция
– квадратичная функция
Квадратичную функцию
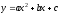 можно задать формулой вида
можно задать формулой вида
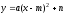 .
.
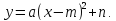 Доказательство.
Выделим из квадратного трёхчлена
Доказательство.
Выделим из квадратного трёхчлена
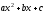 полный квадрат:
полный квадрат:
 .
.
Обозначим
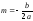 и
и
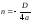 . Получим
. Получим
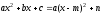
График функции
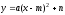 – парабола с вершиной в точке
– парабола с вершиной в точке
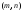 .
Значит, график функции
.
Значит, график функции
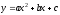 – парабола с вершиной в точке
– парабола с вершиной в точке
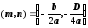 .
.
Ось симметрии параболы – прямая
 .
.
Парабола пересекает ось Oy в точке (0;с)
Пример 6. Построим график функции
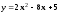 .
.
|
|
Решение. Выделим полный квадрат:
|
Задания для решения
-
Найдите вершину параболы, точку пересечения параболы с осью
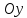 ,
точки пересечения с осью
,
точки пересечения с осью
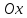 (если такие есть). Схематически постройте
параболу по полученным точкам:
(если такие есть). Схематически постройте
параболу по полученным точкам:

-
Найдите координаты точек пересечения графиков функций:
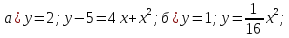
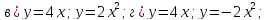
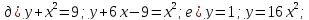
6.6. Системы уравнений с двумя переменными
Пример 7. Сумма квадратов двух чисел равна 25. Разность чисел равна 1. Найдём числа.
Решение. 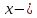 x
– первое число, y
– второе число.
x
– первое число, y
– второе число.
Нужно решить систему уравнений:
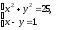
График уравнения
 – окружность радиуса
– окружность радиуса
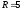 с центром в начале координат. График
уравнения
с центром в начале координат. График
уравнения
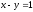 –
– 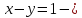 прямая
линия.
прямая
линия.
Окружность и прямая пересекаются в двух точках (рисунок 14.7). Значит, система уравнений имеет два решения.

|
Рисунок 14.7
|
Найдём соответствующие значения переменной y:
Ответ:
|
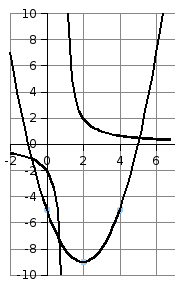
Пример 8. Найдите количество решений системы уравнений графически.

|
Рисунок 14.8 |
Решение. Графики
функций построим схематически.
Гипербола
Гипербола и парабола пересекаются в трёх точках. Значит, система уравнений имеет три решении. Ответ: 3 решения. |
7. Показательная и логарифмическая функции
7.1 Показательная функция
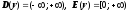
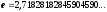 – число е.
– число е.
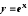 экспонента.
экспонента.
Пример 1. Построим графики функций
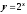 и
и
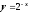 по точкам.
по точкам.
|
|
|
|
|
||||||||||||
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
x |
-2 |
-1 |
0 |
1 |
2 |
|||
|
y |
0,25 |
0,5 |
1 |
2 |
4 |
|
y |
4 |
2 |
1 |
0,5 |
0,25 |
|||
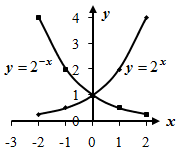
Рисунок 15.1
Графики функций пересекают ось Oy
в точке (0;1). Графики функций
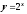 и
и
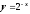 симметричны относительно оси Oy.
Функция
симметричны относительно оси Oy.
Функция
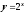 возрастает на всей числовой оси, функция
возрастает на всей числовой оси, функция
 …..
…..

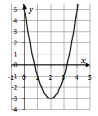
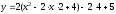
 парабола с вершиной в точке (2; –3).
Ветви параболы направлены вверх.
Парабола пересекает ось Oy
в точке (0;5).
парабола с вершиной в точке (2; –3).
Ветви параболы направлены вверх.
Парабола пересекает ось Oy
в точке (0;5).
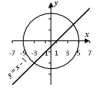
 – корни уравнения
– корни уравнения
 .
.
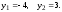
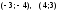 .
.
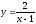 получается смещением гиперболы
получается смещением гиперболы
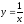 вправо на 1 и растяжением от оси
вправо на 1 и растяжением от оси
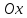 в 2 раза. Вершина параболы
в 2 раза. Вершина параболы
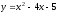 находится в точке
находится в точке
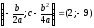 .
Парабола пересекает ось
.
Парабола пересекает ось
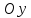 в точке (0;–5) и симметрична относительно
прямой
в точке (0;–5) и симметрична относительно
прямой
 .
.