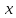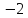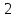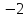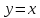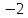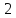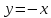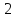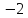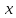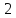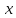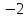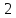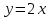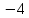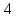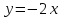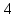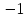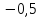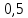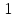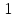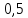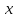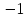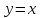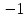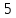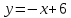- •Оглавление
- •Числовые выражения Свойства дробей
- •Основное свойство дроби
- •Действия с дробями
- •Линейные уравнения и системы линейных уравнений
- •Линейное уравнение с одной переменной
- •Системы линейных уравнений
- •Алгебраические выражения
- •Формулы сокращённого умножения
- •Тождественные преобразования рациональных выражений
- •Задания для решения
- •Квадратное уравнение и его корни
- •Задания для решения
- •Теорема Виета
- •Задания для решения
- •3.5. Уравнения, сводящиеся к квадратным
- •Задания для решения
- •Множества
- •4.1 Числовые множества
- •4.2 Операции над множествами
- •Пересечение множеств
- •Объединение множеств
- •Разность множеств
- •Задания для решения
- •Прямоугольная система координат
- •Прямоугольные координаты точки
- •Функции
- •6.1. Основные понятия
- •6.2. Функции
- •Задания для решения
- •6.3 Линейная функция
- •Задания для решения
- •6.4. Функции , ,
- •Задания для решения
- •6.5. График и свойства квадратичной функции
- •Задания для решения
- •6.6. Системы уравнений с двумя переменными
- •7. Показательная и логарифмическая функции
- •7.1 Показательная функция
- •Задания для решения
- •7.2 Показательные уравнения
- •7.3.Логарифмическая функция ,
- •Задания для решения
- •7.4. Показательные и логарифмические уравнения
- •Задания для решения
- •Геометрические фигуры на плоскости
- •Треугольники
- •Задания для решения
- •Четырёхугольники
- •Задания для решения
- •Окружность и круг
- •Задания для решения
- •9. Элементы тригонометрии
- •9.1 Таблица значений тригонометрических и обратных тригонометрических функций
- •9.2 Графики тригонометрических функций
- •Задания для решения
- •9.3 Тригонометрические преобразования и уравнения
- •Задания для решения
- •Арифметическая и геометрическая прогрессии
- •10.1 Арифметическая прогрессия
- •10.2 Геометрическая прогрессия
- •Варианты заданий
6.2. Функции
Функция

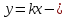 – прямая пропорциональная зависимость.
– прямая пропорциональная зависимость.
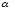

График функции
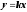
 – прямая (линия).
– прямая (линия).
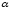

График проходит через начало координат
– точку
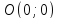 .
.
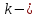
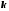
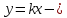 – угловой коэффициент прямой.
– угловой коэффициент прямой.


Область
определения – вся числовая ось:
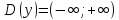 .
.
Область
значений – вся числовая ось:
 .
.
|
|
Функция
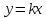 нечётная, так как
нечётная, так как
 .
.
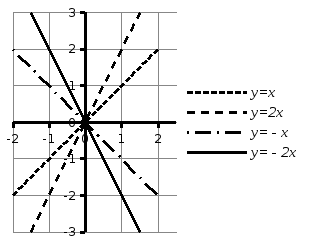
Пример 1. В системе координат
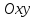 начертим графики функций
начертим графики функций
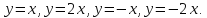 Для построения прямой линии необходимо
две точки. Зададим таблицы значений.
Для построения прямой линии необходимо
две точки. Зададим таблицы значений.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция
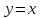 возрастает, т.к.
возрастает, т.к.
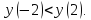
Функция
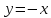 убывает,
т.к.
убывает,
т.к.
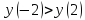 .
.
|
Рисунок 11.9 |
Функция 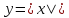
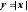
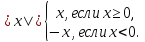
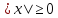
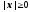 для любого x
для любого x
Функция
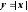 чётная, т.к.
чётная, т.к.
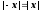 .
.

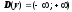 область определения,
область определения, 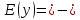
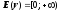 область значений.
область значений.
График функции 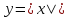
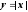 симметричен относительно оси
симметричен относительно оси
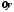
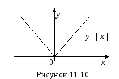
Построение графиков методом преобразований
Функция
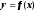 ,
,
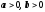 ,
,
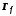 – график функции
– график функции
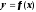 .
.
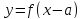
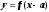
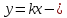 смещение
смещение
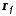 на
a вправо.
на
a вправо.
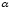


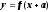
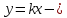 смещение
смещение
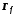 на
a влево.
на
a влево.
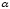

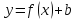
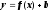
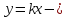 смещение
смещение
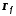 на b вверх.
на b вверх.
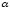

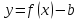
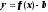
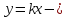 смещение
смещение
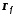 на b вниз.
на b вниз.
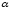

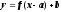
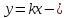 смещение
смещение
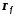 на
a вправо и на b
вверх
на
a вправо и на b
вверх
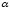

Пример 2. Построим графики функций
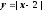 и
и
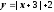 .
.
-

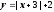 .
Смещение графика функции
.
Смещение графика функции 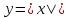
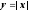 на 3 влево и на 2 вверх. Функция
на 3 влево и на 2 вверх. Функция
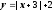 убывает при
убывает при
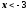 и возрастает при
и возрастает при 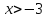
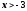 .
.

Рисунок 11.11
-
Постройте график функции:
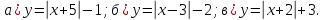
Функция 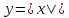
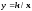 задаёт обратную пропорциональную
зависимость.
задаёт обратную пропорциональную
зависимость.
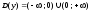
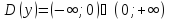 область
определения.
область
определения.
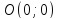
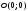 точка разрыва функции.
точка разрыва функции.
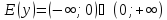
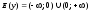 область значений.
область значений.
График функции называется гипербола.
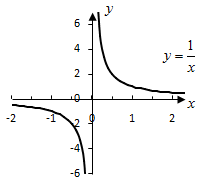


Рисунок 11.12
Пример 3. Построим график функции
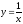 по точкам. Зададим таблицу значений:
по точкам. Зададим таблицу значений:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция
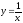 убывает. Функция нечётная.
убывает. Функция нечётная.
График функции
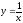 симметричен относительно начала
координат – точки
симметричен относительно начала
координат – точки
 .
.
Задания для решения
-
На одной координатной плоскости методом преобразований постройте графики функций
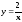 ,
,
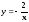 ,
,
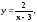
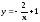 .
.
6.3 Линейная функция

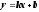 линейная функция.
линейная функция.
График линейной функции – прямая
(линия). 
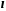 обозначение прямой.
обозначение прямой.
Прямая
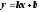 пересекает ось
пересекает ось 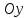
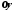 в точке b. k
– угловой коэффициент прямой.
в точке b. k
– угловой коэффициент прямой.
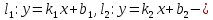 две прямые.
две прямые.
-
Прямые
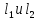 параллельны, если
параллельны, если 
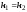 .
.
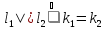
-
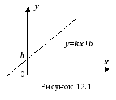
Прямые
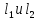
 пересекаются, если
пересекаются, если
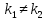 .
.
 прямые
прямые
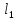 и
и
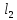 пересекаются в точке A.
пересекаются в точке A.
-
Прямые
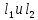 перпендикулярны, если
перпендикулярны, если 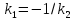
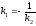 .
.
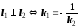
Пример 1. В системе координат
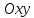 построим прямые
построим прямые
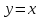 и
и
 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
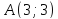 – точка пересечения прямых.
– точка пересечения прямых.
Прямые перпендикулярны, т.к.
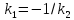 ,
,
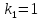 ,
,
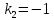 .
.
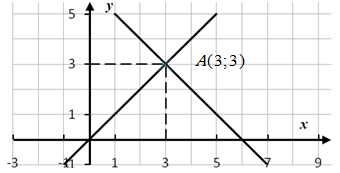
Рисунок 12.2