
- •Оглавление
- •Числовые выражения Свойства дробей
- •Основное свойство дроби
- •Действия с дробями
- •Линейные уравнения и системы линейных уравнений
- •Линейное уравнение с одной переменной
- •Системы линейных уравнений
- •Алгебраические выражения
- •Формулы сокращённого умножения
- •Тождественные преобразования рациональных выражений
- •Задания для решения
- •Квадратное уравнение и его корни
- •Задания для решения
- •Теорема Виета
- •Задания для решения
- •3.5. Уравнения, сводящиеся к квадратным
- •Задания для решения
- •Множества
- •4.1 Числовые множества
- •4.2 Операции над множествами
- •Пересечение множеств
- •Объединение множеств
- •Разность множеств
- •Задания для решения
- •Прямоугольная система координат
- •Прямоугольные координаты точки
- •Функции
- •6.1. Основные понятия
- •6.2. Функции
- •Задания для решения
- •6.3 Линейная функция
- •Задания для решения
- •6.4. Функции , ,
- •Задания для решения
- •6.5. График и свойства квадратичной функции
- •Задания для решения
- •6.6. Системы уравнений с двумя переменными
- •7. Показательная и логарифмическая функции
- •7.1 Показательная функция
- •Задания для решения
- •7.2 Показательные уравнения
- •7.3.Логарифмическая функция ,
- •Задания для решения
- •7.4. Показательные и логарифмические уравнения
- •Задания для решения
- •Геометрические фигуры на плоскости
- •Треугольники
- •Задания для решения
- •Четырёхугольники
- •Задания для решения
- •Окружность и круг
- •Задания для решения
- •9. Элементы тригонометрии
- •9.1 Таблица значений тригонометрических и обратных тригонометрических функций
- •9.2 Графики тригонометрических функций
- •Задания для решения
- •9.3 Тригонометрические преобразования и уравнения
- •Задания для решения
- •Арифметическая и геометрическая прогрессии
- •10.1 Арифметическая прогрессия
- •10.2 Геометрическая прогрессия
- •Варианты заданий
-
Алгебраические выражения
-
Формулы сокращённого умножения
-
-
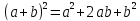 квадрат суммы a и b
квадрат суммы a и b
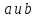 равен
квадрату первого члена плюс удвоенное
произведение первого члена на второй
плюс квадрат второго члена;
равен
квадрату первого члена плюс удвоенное
произведение первого члена на второй
плюс квадрат второго члена; -
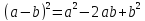 квадрат разности a и
b;
квадрат разности a и
b; -
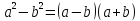 разность
квадратов;
разность
квадратов; -
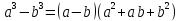 разность кубов;
разность кубов; -
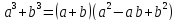 сумма кубов;
сумма кубов; -
 куб суммы;
куб суммы;
-
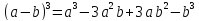 куб разности.
куб разности.
-
Тождественные преобразования рациональных выражений
Пример. Найдём
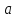 и
и
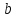 из тождества:
из тождества:
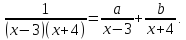
Приведём дроби к общему знаменателю:
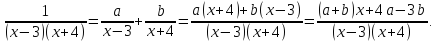
Дроби
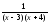 и
и
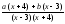 равны, их знаменатели равны. Значит,
равны числители:
равны, их знаменатели равны. Значит,
равны числители:
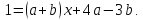
Приравняем коэффициенты при одинаковых степенях х:
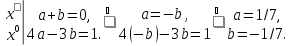
Пример 4. Выполним деление многочленов
с остатком:
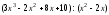 .
.
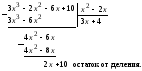
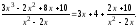
Пример 5. Выполним деление многочленов без остатка:
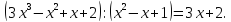
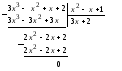
Задания для решения
-
Упростите выражение:

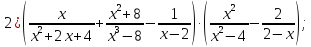
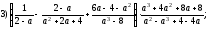
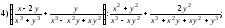
-
Найдите
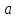 и
и
 из тождества:
из тождества:
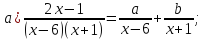
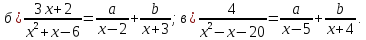
-
Выполните деление многочленов с остатком:
а)
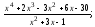 б)
б)
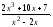
-
Сократите дроби:


-
Квадратное уравнение и его корни
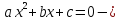 квадратное уравнение
квадратное уравнение
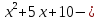
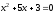 приведённое квадратное уравнение,
приведённое квадратное уравнение,
Рассмотрим квадратное уравнение

Получим равносильное приведённое квадратное уравнение
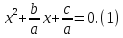
Выделим полный квадрат:
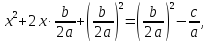

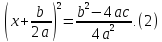
Уравнения (1) и (2) имеют одинаковые корни.
 дискриминант.
дискриминант.

-
 уравнение имеет 2 различных действительных
корня.
уравнение имеет 2 различных действительных
корня.
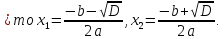
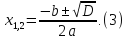
(3) – формула корней квадратного уравнения.
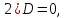 то уравнение (2) принимает вид:
то уравнение (2) принимает вид:
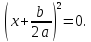
В этом случае уравнение (1) имеет два одинаковых корня
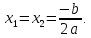
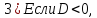 то уравнение
то уравнение

не имеет действительных корней.
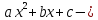 квадратный трёхчлен.
квадратный трёхчлен.
Квадратный трёхчлен
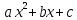 можно разложить на множители вида:
можно разложить на множители вида:
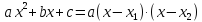 ,
,
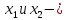 корни уравнения
корни уравнения
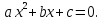
Задания для решения
-
Разложите квадратный трёхчлен на множители:
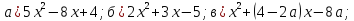
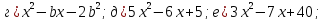
-
Теорема Виета
Теорема Виета:
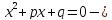 приведённое квадратное уравнение. Тогда
сумма корней
приведённое квадратное уравнение. Тогда
сумма корней
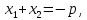 произведение корней
произведение корней

Доказательство:
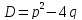 .
.
Если
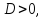 то уравнение имеет два корня:
то уравнение имеет два корня:
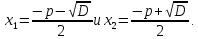
Найдём сумму и произведение корней:
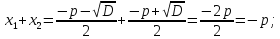
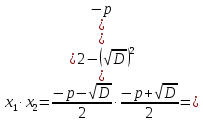

Задания для решения
-
Найдите сумму и произведение корней уравнения:
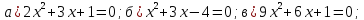
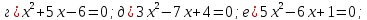
3.5. Уравнения, сводящиеся к квадратным
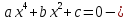 биквадратное уравнение.
биквадратное уравнение.
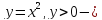 новая переменная.
новая переменная.
Получим квадратное уравнение
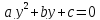 .
.
Пример 3. Решим биквадратное уравнение
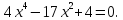
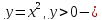 новая переменная.
новая переменная.
Получим квадратное уравнение
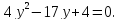
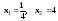 – корни квадратного уравнения,
– корни квадратного уравнения,
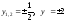 – корни биквадратного уравнения.
– корни биквадратного уравнения.
Пример 4. Решим уравнение
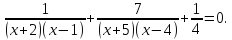
ОДЗ:
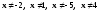 .
(1)
.
(1)
Выполним умножение в знаменателях дробей и получим:
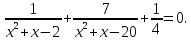
Введём новую переменную
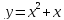 .
Получим уравнение.
.
Получим уравнение.
 , (2)
, (2)
ОДЗ:
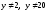 . (3)
. (3)
Умножим уравнение (2) на
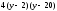 .
Получим
.
Получим
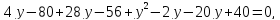
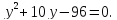
Корни этого уравнения
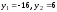 удовлетворяют условиям (3). Значит,
удовлетворяют условиям (3). Значит,
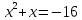 или
или
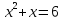 .
.
Уравнение
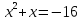 не имеет корней.
не имеет корней.
Уравнение
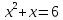 имеет корни
имеет корни
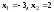 ,
которые условиям (1). Значит, исходное
уравнение имеет два корня:
,
которые условиям (1). Значит, исходное
уравнение имеет два корня: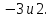
Ответ: :
Задания для решения
-
Решите уравнение с помощью замены переменной:
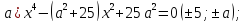
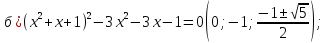
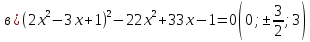
-
Решите уравнение с помощью замены переменной:
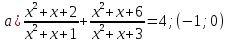
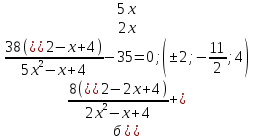
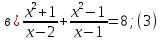
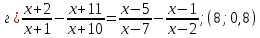
-
Множества
4.1 Числовые множества
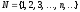 множество натуральных чисел
множество натуральных чисел
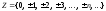
 множество целых чисел
множество целых чисел
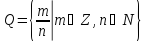 множество рациональных чисел.
множество рациональных чисел.
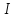 множество иррациональных чисел.
множество иррациональных чисел.
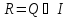 множество действительных чисел.
множество действительных чисел.
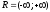
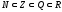 ,
,
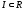 - отношения включения между множествами.
- отношения включения между множествами.
4.2 Операции над множествами
Рассмотрим множества:
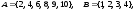

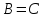
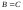 множество B
множество B  равно множеству C
равно множеству C
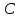 ,
т.к. B и C
состоят из одинаковых элементов.
,
т.к. B и C
состоят из одинаковых элементов.
 D подмножество A,
т.к. элементы множества D
принадлежат множеству A.
D подмножество A,
т.к. элементы множества D
принадлежат множеству A.
 пустое множество.
пустое множество.
Пустое множество  не содержит элементов.
не содержит элементов.
