Лабораторная № 1.

3.1. Дать определения:

Абсолютная погрешность измерения  - разность между результатом измерения Х и истинным значением Хo измеряемой величины:

Абсолютная погрешность выражается в единицах измеряемой величины. Относительная погрешность измерения  - отношение абсолютной погрешности измерения  к истинному значению измеряемой величины Хo:

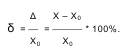
Относительная погрешность - безразмерная величина. Поскольку истинное значение измеряемой величины Хo неизвестно, то практически используют действительное значение измеряемой величины Хд, и тогда погрешность определяется как разность между измеренным Х и действительным значением Хд:

Действительное значение находят экспериментально, путем применения более точных методов и средств измерений. Обычно за действительное значение принимают показания образцовых средств измерения. Значение относительной погрешности  на практике определяется как отношение абсолютной погрешности к действительному значению:

Приведенная погрешность измерения  - это отношение абсолютной погрешности  к нормирующему значению Хn:

Систематическая погрешность - постоянная или закономерно изменяющаяся погрешность при повторных измерениях одной и той же величины в одинаковых условиях измерения.

Дополнительная погрешность обуславливается отклонением одной или нескольких влияющих величин от нормального значения. 

Основная погрешность - погрешность, возникающая в нормальных условиях применения средства измерения (температура, влажность, напряжение питания и др.), которые нормируются и указываются в стандартах или технических условиях.

Аддитивная погрешность – это погрешность, возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (абсолютного).

Мультипликативная погрешность – это погрешность, изменяющаяся вместе с изменением значений величины, подвергающейся измерениям.

3.2. Как оценить систематическую составляющую погрешности прибора?

Оценку систематических погрешностей можно получить по характеристикам используемого прибора (по паспортным данным или из свидетельства о поверке) и метода измерения (путем его анализа). Из документации на прибор можно оценить и учесть дополнительные систематические погрешности.

Систематические погрешности в ряде случаев можно определить экспериментальным путем. Результат измерений тогда можно уточнить посредством введения поправки.

Способы исключения систематических погрешностей делятся на четыре вида:

1) ликвидация причин и источников погрешностей до начала проведения измерений;

2) устранение погрешностей в процессе уже начатого измерения способами замещения, компенсации погрешностей по знаку, противопоставлениям, симметричных наблюдений;

3) корректировка результатов измерения посредством внесения поправки (устранение погрешности путем вычислений);

4) определение пределов систематической погрешности в случае, если ее нельзя устранить.

3.3. Как оценить доверительный интервал случайной погрешности однократного измерения при заданной доверительной вероятности и нормальном законе распределения?

Симметричный интервал в границами ± Δх(Р) называетсядоверительным интервалом случайной погрешности с довери-тельной вероятностью Р.

Доверительный интервал для нормального распределения находится по формуле:                                   где коэффициент t зависит от доверительной вероятности Р. Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999).