Задачи.

4.1. Сравните действительные числа и : 1) а = 1,(1234512), b = 1,(12345); 2) а = 1,0(123), b = 1,0(1231).

4.2. Рациональное число запишите в виде десятичной дроби.

4.3. Запишите бесконечные периодические десятичные дроби в виде обыкновенных дробей: 1) 0,(7); 2) 2,4(31).

4.4. Какое из чисел больше: 1) а или –а; 2) а или , если а≠0?

4.5. Докажите, что число log₂3 является иррациональным.

4.6. Найдите точные верхние и нижние границы мнжеоств: 1) {n}; 2){ }; 3) {}; 4) {} ().

4.7. Докажите, что нуль является нижней границей множеств: 1) ; 2) .

4.8. Найдите такие действительные числа x и y так, чтобы , если .

4.9. Вычислить произведение и частное , если: 1) ; 2) .

4.10. Разрешите систему уравнений .

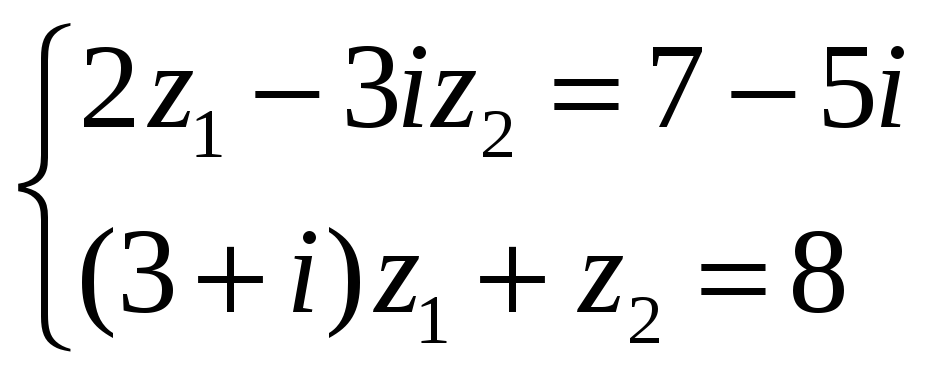4.11. Изобразите на комплексной плоскости множество точек, удовлетворяющих условиям: 1) ; 2) .

Домашнее задание 4.

4.12. Найдите сумму a + b действительных чисел а = 0,(51), b = 0,(53).

4.13. Сравните действительные числа и .

4.14. Зная, что числа и – иррациональные, докажите иррациональность числа .

4.15. Докажите, что нуль является нижней границей множеств: 1) ; 2) .

4.16. Разрешите систему уравнений .

4.17. Изобразите на комплексной плоскости множество точек, удовлетворяющих условию .

Занятие 5.Тригонометрическая форма комплексного числа.

Модулем комплексного числа z называется длина соответствующего ему вектора. Модуль числа обозначается |z| и вычисляется по формуле

. (1)

Аргументом комплексного числа называется угол угол между положительным направлением действительной оси и вектором z. Для числа аргумент не определяется. Аргумент комплекного числа z обозначается и определяется с точностью до слагаемого, кратного 2π.

Из геометрических соображений несложно представить действительную и мнимую части комплексного числа через его модуль r и аргумент :

, (2)

Откуда следует . (3)

Аргументы комплексного числа можно вычислить из уравнения , которое является следствием системы (3). Это уравнение имеет больше решений, чем система (3), но выбрать нужные решения (аргументы комплексного числа) можно по правилу: если , (т.е. число z расположено в правой полуплоскости), то ; если Rez<0, (т.е. число z расположено в левой полуплоскости), то .

Из равенств (2) следует, что камплексное число можно представить в виде , где . Такое представление комплексного числа называется тригонометрической формой комплексного числа. Тригонометрическая форма является исключительно удобной для умножаения и деления комплексных чисел.

Если , , то

, .

На основании этих равенств выводится формула возведения в степень

,

частный случай которой называется формулой Муавра.

Камплексное число w называется корнем степени n из комплекного числа z и обозначается , если . Если , то существубт n значений корня степени n из числа z, которые находятся по формуле

. (4)

Комплексные числа, являющиеся корнями степени n из числа z, соответствуют точкам комплекcной плоcкости, расположенным в вершинах правильного n-угольника, вписанного в окружность радиуса с центром в точке О.

Пример 1. Определить аргументы комплексных чисел .

▶ Поскольку , то . В то же время , а поэтому . ◄

Пример 2. Найти модули и аргументы чисел

.

▶ Для нахождения модулей и аргументов чисел и совсем необязательно пользоваться формулами (1) и (3). На основании формул приведения выполним следующие преобразования:

Поскольку и представлены в тригонометрической форме, то

. ◄

Пример 3. Записать в тригонометрической форме комплексное число

.

▶ Поскольку число имеет ||=1 и arg , число = мае ||=4 и , а число = имеет ||=2 и , то

, . Поэтому . ◄

Пример 4. Вычислить .

▶ При вычислении корня квадратного часто бывает более удобно использовать вместо формулы (4) определение корня второй степени из комплексного числа. Пусть , тогда 5–12i = . Числf а и b определяются из системы уравнений решения которой (–3; 2) и (3; –2). Таким образом, комплексные числа и , являются двумя значениями . ◄