
- •Пример. Вычислить сумму .
- •Домашнее задание 1.
- •Занятие 2. Метод математической индукции.
- •Пример 1. Доказать, что сумма первых n нечётных чисел () равна .
- •Пример 2. Найти все натуральные числа n, для которых верно неравенство
- •Задачи.
- •Домашнее задание 2.
- •Занятие 3. Элементы комбинаторики. Формула бинома Ньютона.
- •Пример . Сколько шестизначных чисел, кратных 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?
- •Задачи.
- •Домашнее задание 3.
- •Занятие 4. Действительные и комплексные числа.
- •Задачи.
- •Домашнее задание 4.
- •Занятие 5.Тригонометрическая форма комплексного числа.
- •Задачи.
- •Домашнее задание 5.
- •Занятие 6. Многочлены и рациональные дроби.
- •Пример 1. Решить уравнение .
- •Пример 2. Решить уравнение .
- •Пример 3. Записать многочлен в виде произведения двух многочленов второй степени с действительными коэффициентами.
- •►1) По формуле (3) представим: .
- •Задачи.
- •Домашнее задание 6.
- •Занятие 7. Функции и последовательности. Задачи
- •Домашнее задание 7.
- •Занятие 8. Предел последовательности. Задачи
- •Домашнее задание 8.
- •Занятие 9. Доказательство пределов. Задачи
- •Домашнее задание 9.
- •Занятие 10. Контрольная работа №1. Самоподготовка.
- •Занятие 11. Предел функции. Задачи
- •Домашнее задание 13.
- •Занятие 14. Сравнение функций. Вычисление пределов. Задачи
- •Домашнее задание 14.
- •Занятие 15. Производная, дифференциал, геометрический смысл. Задачи
- •Домашнее задание 15.
- •Занятие 16. Дифференцирование композиции. Задачи
- •Домашнее задание 16.
- •Домашнее задание 18.
- •Занятие 21. Неопределённый интеграл.
- •Домашнее задание 21.
- •Домашнее задание 28.
- •Занятие 29. Длина кривой. Объём тела вращения. Задачи
- •Домашнее задание 30.
- •Занятие 31. Контрольная работа №3. Самоподготовка.
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ РАДИОФИЗИКИ И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ И МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Виктор Ахраменко
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ.
1 семестр.
Методическое пособие по практическим занятиям для студентов первого курса
МИНСК
2011
Занятие 1. Множества. Суммирование.
1º. Множество
– первичное (неопределяемое)
понятие. Обозначают
множества большими
буквами A,
B, C,
X,.![]() ..;
..;
![]() – множество натуральных
чисел,
– множество натуральных
чисел,
![]() – целых,
– целых,
![]() – рациональных,
– рациональных,
![]() – действительных.
Принадлежность элемента x
множеству A обозначают
x
– действительных.
Принадлежность элемента x
множеству A обозначают
x![]() A;
если x не является
элементом A ,
то пишут x
A;
если x не является
элементом A ,
то пишут x![]() А.
Используют также запись:
А.
Используют также запись:
![]() ,
паказывающую, что
,
паказывающую, что
![]() являются элементами
множества X (и только
они); а также
X={x:
Р(x)},
которая характеризирует
множество X
как совокупность
элементов x,
удовлетворяющих условию
Р(x).
являются элементами
множества X (и только
они); а также
X={x:
Р(x)},
которая характеризирует
множество X
как совокупность
элементов x,
удовлетворяющих условию
Р(x).
Если каждый
элемент множества А является
элементом множества В,
то говорят:
"А
является подмножеством
множества В" или "
А содержится в В
" и пишут А![]() В
(или В
В
(или В![]() А).
Два множества А и В
называются равными
(обозначают
А).
Два множества А и В
называются равными
(обозначают
![]() ),
если они состоят
из одних и
тех же
элементов:
),
если они состоят
из одних и
тех же
элементов:
![]() ,
если и тольки если
,
если и тольки если
![]()
![]() и
и
![]() .
Множество, не имеющее
элементов, называется
пустым и обозначается
.
Множество, не имеющее
элементов, называется
пустым и обозначается
![]() .
.
Операции
над множествами определяются
следующим образом: 1)
пересечение
множеств
![]() ;
2)объединение
множеств
;
2)объединение
множеств
![]() ;
3) разность
множеств
;
3) разность
множеств
![]() .
.
2º.
Сумма заданных
![]() чисел
чисел
![]() записвается
записвается
![]() .
Буква
.
Буква
![]() называется индексом
суммирования.
Сумма не зависит
от того,
какой буквой
обозначен индекс
суммирования,
т.е.
называется индексом
суммирования.
Сумма не зависит
от того,
какой буквой
обозначен индекс
суммирования,
т.е.
 .
Иногда возникает
необходимость сдвинуть
границы изменения
индекса суммирования
в ту или иную
сторону. Например,
.
Иногда возникает
необходимость сдвинуть
границы изменения
индекса суммирования
в ту или иную
сторону. Например,
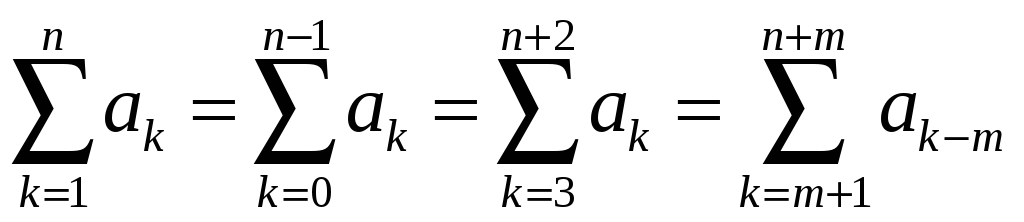 .
Операция суммирования
имеет свойство
линейности
.
Операция суммирования
имеет свойство
линейности
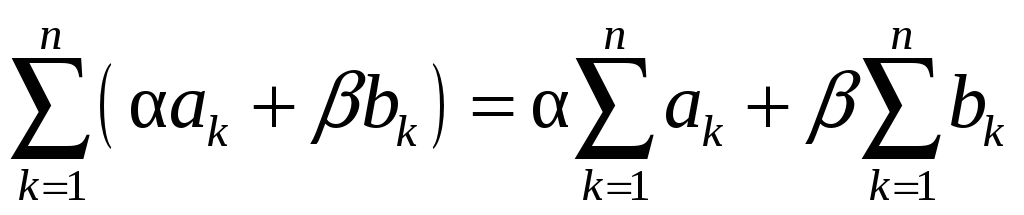 .
Сумму
.
Сумму
![]() склагаемых
склагаемых
![]() записвают в
виде
записвают в
виде
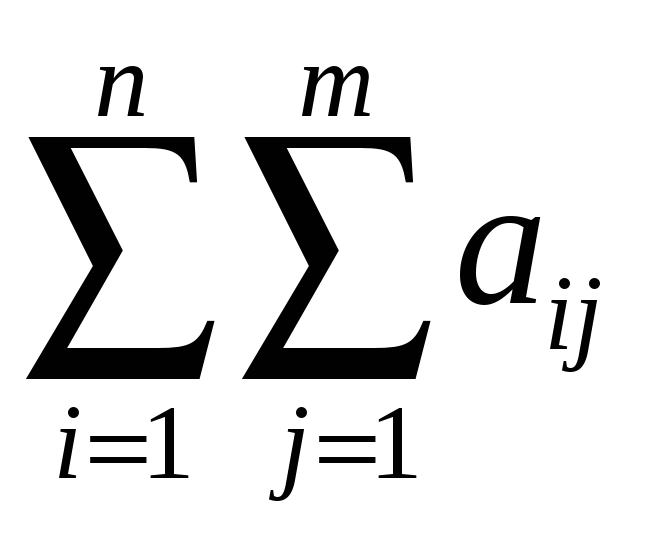 и называют двойной
суммой.
При этом
имеет место
равенство
и называют двойной
суммой.
При этом
имеет место
равенство
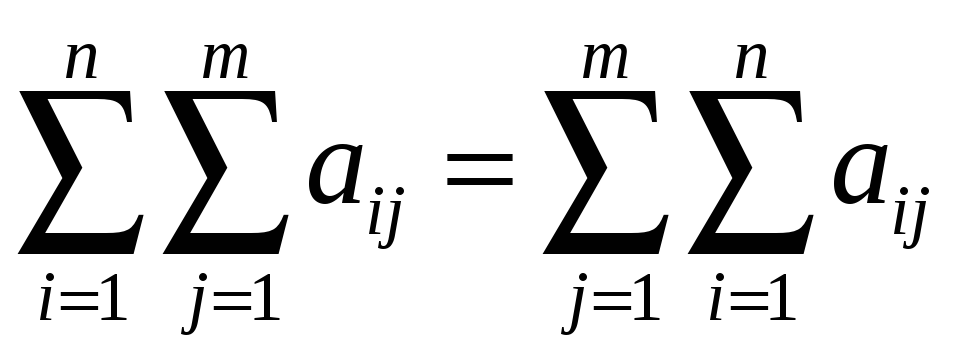 .
.
Пример. Вычислить сумму .
► Задачу о
вычислении
суммы
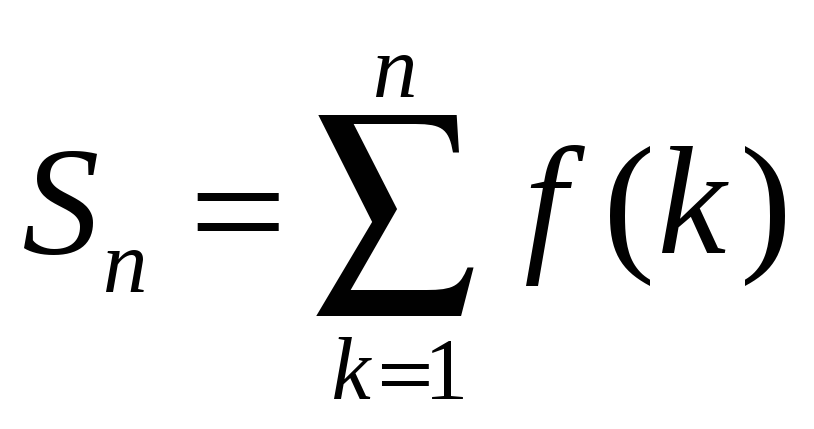 ,
где
,
где
![]() – заданная
функция,
обычно
рассматривают
как
задачу нахождения
– заданная
функция,
обычно
рассматривают
как
задачу нахождения
![]() как
функции
от
как
функции
от
![]() .
Например, если
.
Например, если
![]() ,
то
,
то
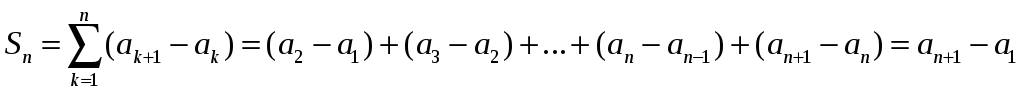 .
.
Посколку
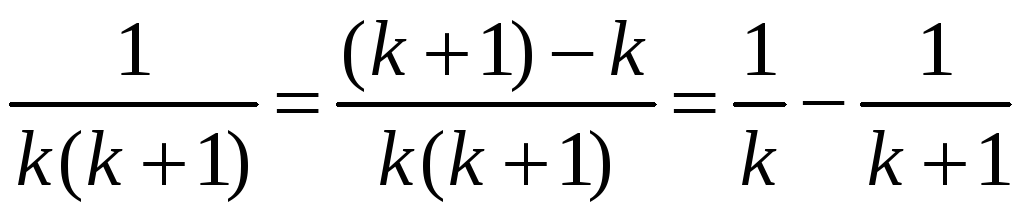 ,
то
,
то
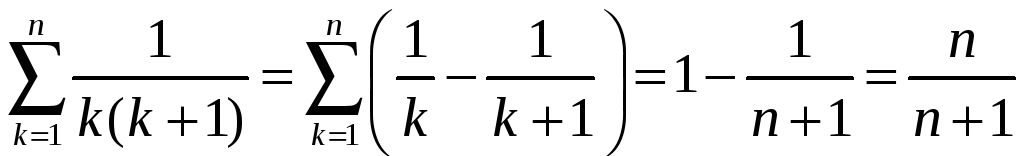 .
◄
.
◄
Задачи
1.1.
Даны
множества
![]() .
Используя операции объединения и
пересечения,
запишите
множество, состоящее из элементов,
принадлежащих: 1) всем трём
множествам; 2) хотя бы одному множеству;
3) по крайней мере двум из этих
множеств.
.
Используя операции объединения и
пересечения,
запишите
множество, состоящее из элементов,
принадлежащих: 1) всем трём
множествам; 2) хотя бы одному множеству;
3) по крайней мере двум из этих
множеств.
1.2.
Пусть А
– множество делителей числа 15; В
– множество простых чисел,
меньших
10; С –
множество чётных чисел, меньших 9. Найдите
множества:
1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ;
4)
;
4) ![]() ;
5)
;
5) ![]() ;
6)
;
6)
![]() .
.
1.3.
Укажите
множества
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
если:
1)
,
если:
1)![]() ;
2)
;
2)![]() ;
3)
;
3)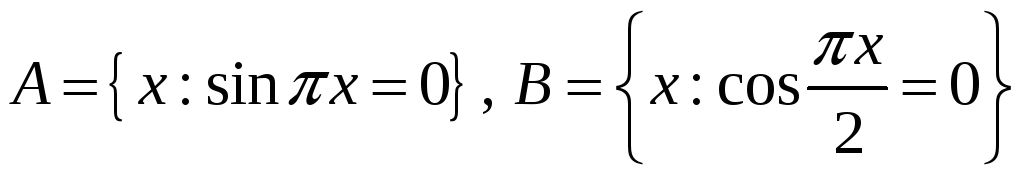 ;
4)
;
4)![]() ;
5)
;
5)![]() .
.
1.4.
Укажите
множество
![]() ,
если: 1)
,
если: 1)
![]() ;
2)
;
2)![]() где
где
![]() .
.
1.5.
Вычислить:
1)
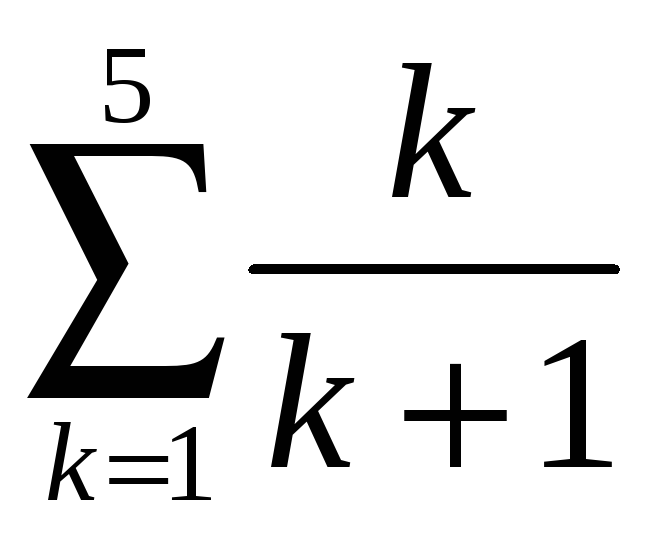 ;
2)
;
2)
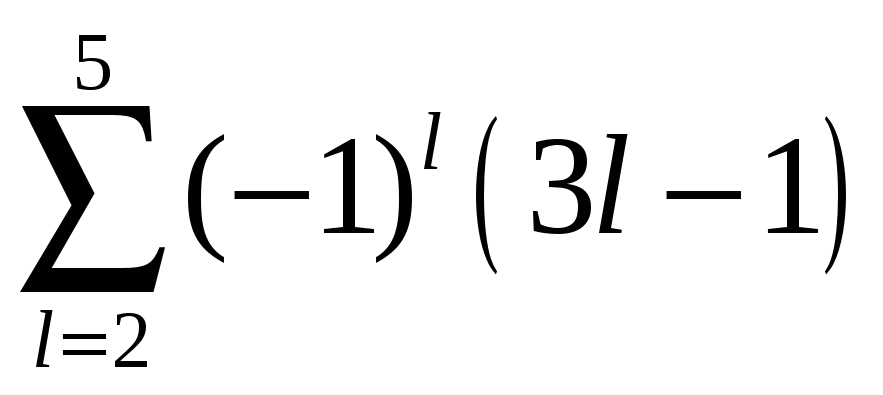 ;
3)
;
3)
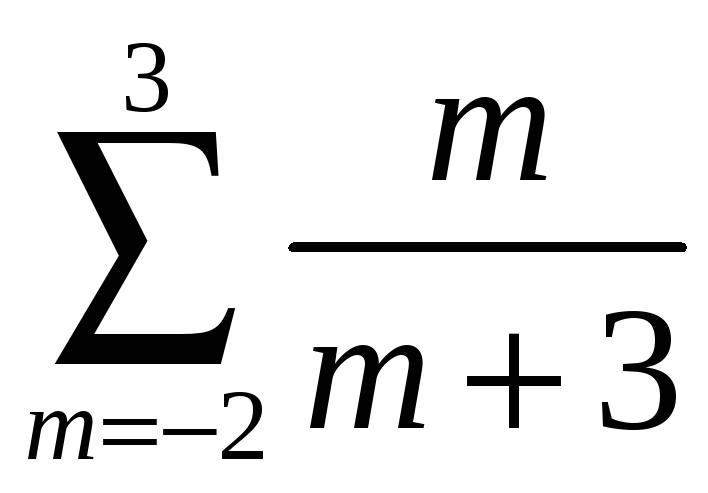 ;
4)
;
4)
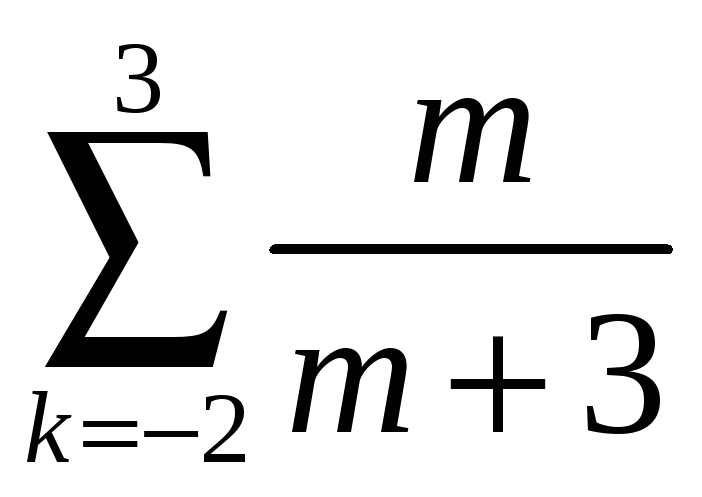 .
.
1.6.
Верно ли
равенство
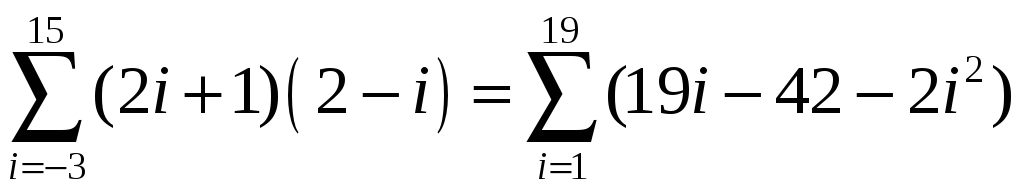 ?
?
1.7.
Вычислить:
1) 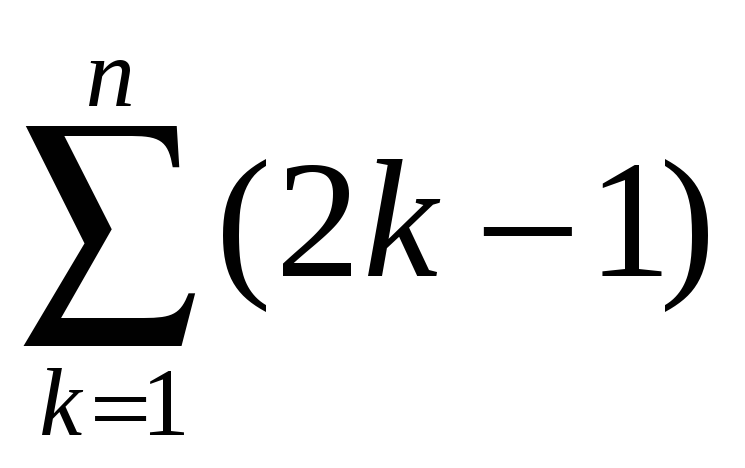 ;
2)
;
2) ![]() ;
3)
;
3) 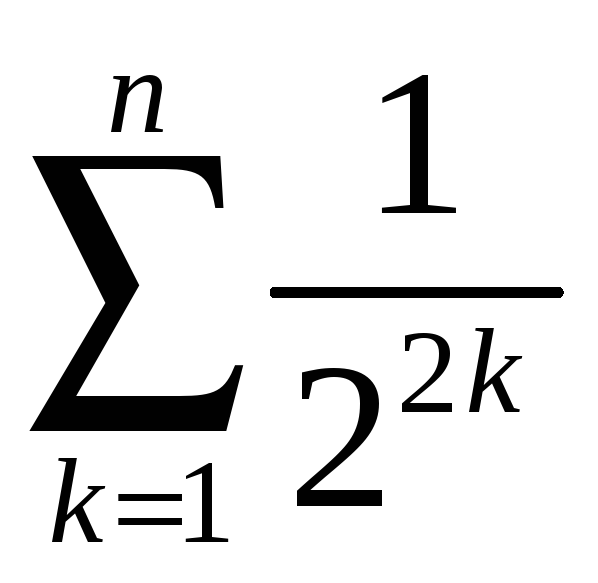 .
.
1.8.
Вычислить
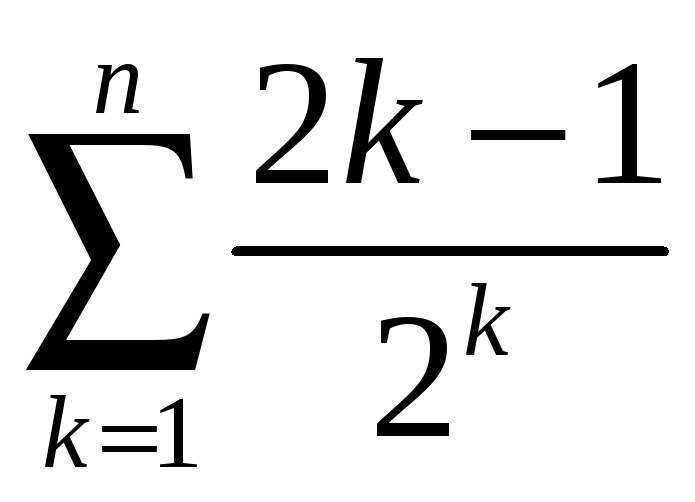 .
.
1.9.
Вычислить:
1)  ;
2)
;
2) 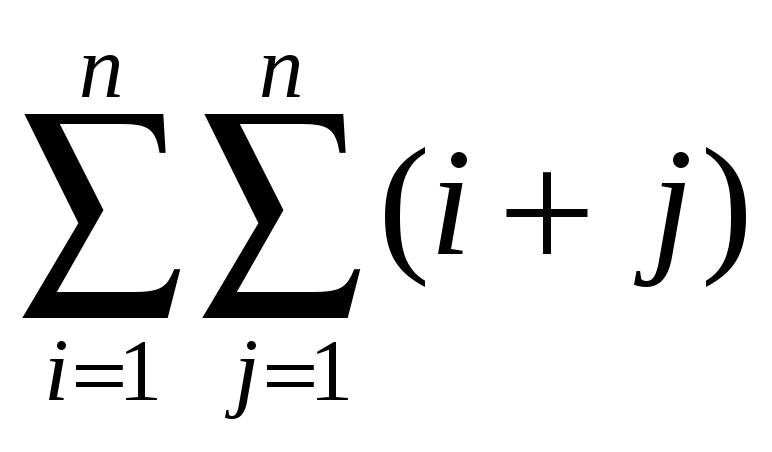 .
.
1.10.
Вычислить
1) 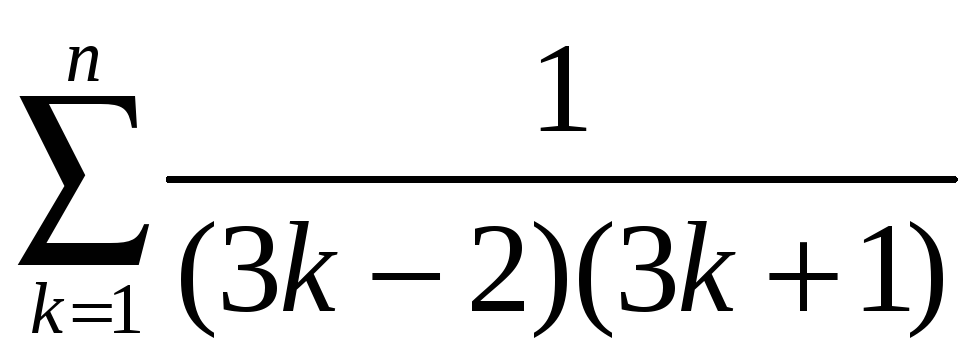 ;
2)
;
2) 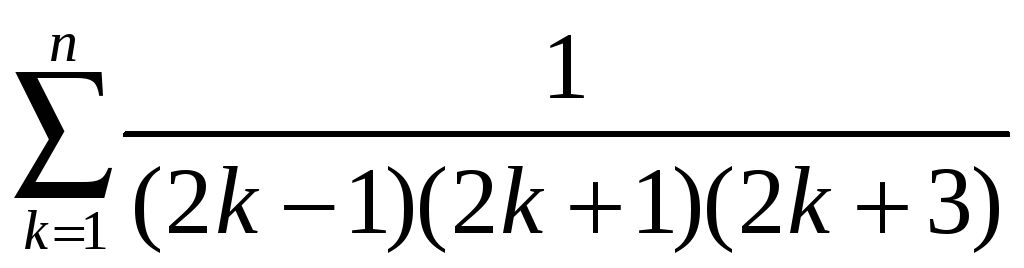 .
.
Домашнее задание 1.
1.11.
Определите
множества
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
если: 1)
,
если: 1)![]() ;
2)
;
2)![]() .
.
1.12.
Определите
множество
![]() ,
если:
1)
,
если:
1)
![]() ;
2)
;
2)
![]() .
.
1.13.
Вычислить:
1)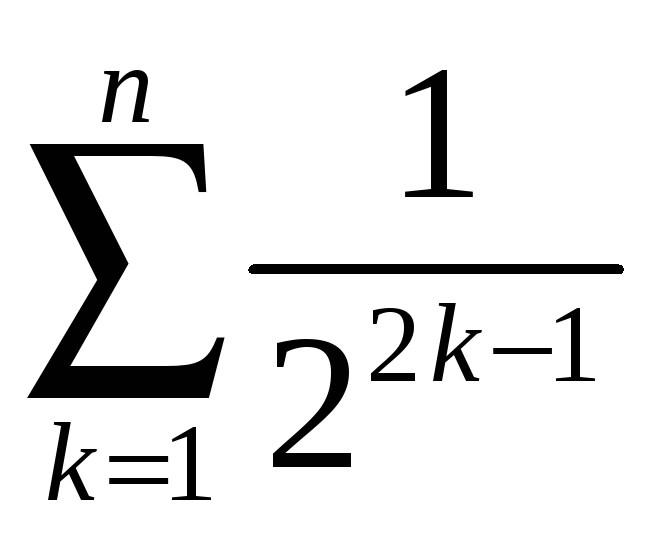 ;
2)
;
2)
 .
.
1.14.
Вычислить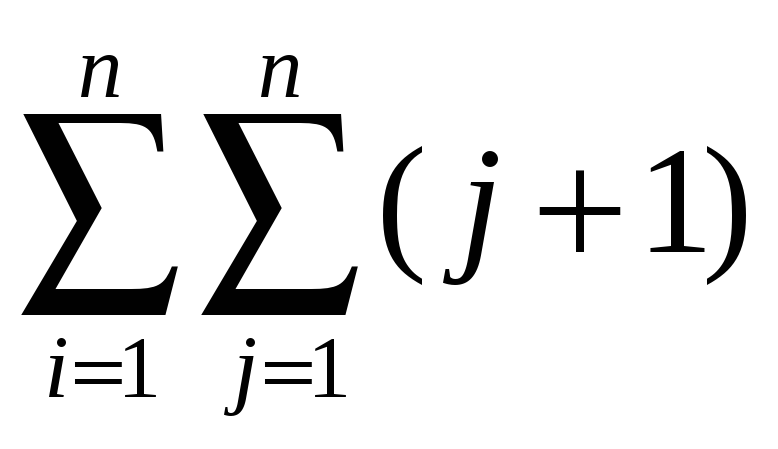 .
.
1.15.
Вычислить
1) 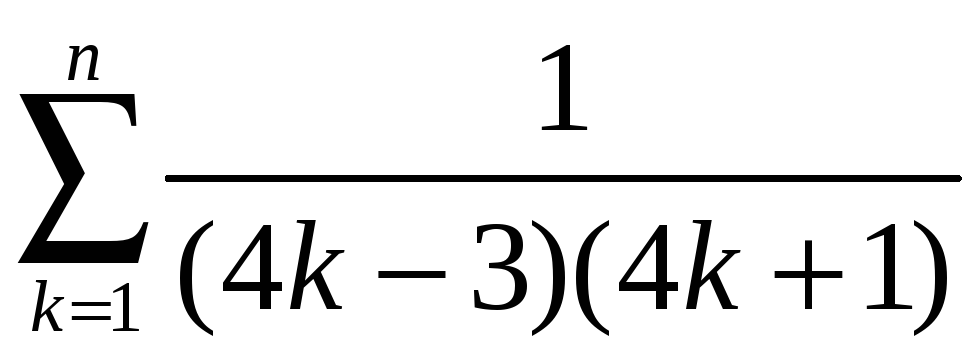 ;
2)
;
2)
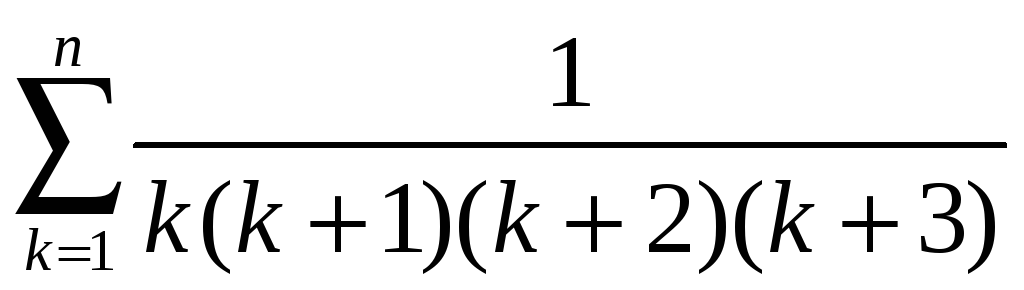 .
.
Занятие 2. Метод математической индукции.
1º. Для
доказательства истинности утверждения
![]() часто используют метод математической
индукции : утверждение
часто используют метод математической
индукции : утверждение
![]() считают истинным при всех
считают истинным при всех
![]() ,
если выполняются
следующие два
условия: 1) высказввание
,
если выполняются
следующие два
условия: 1) высказввание
![]() истинно при
истинно при
![]() ;
2) из истинности
высказывания
;
2) из истинности
высказывания
![]() следует истинность
высказывания
следует истинность
высказывания
![]() при всех
натуральных k. Условие
истинности высказывания
при всех
натуральных k. Условие
истинности высказывания
![]() ,
называется базой
индукции,
а предположение истинности
высказывания
,
называется базой
индукции,
а предположение истинности
высказывания
![]() – индуктивным
соглашением.
Если задачей обусловлено, что высказывание
– индуктивным
соглашением.
Если задачей обусловлено, что высказывание
![]() рассматривается начиная
с некоторого
числа
рассматривается начиная
с некоторого
числа
![]() (не с числа
1), то базой индукции
является истинность
высказывания
(не с числа
1), то базой индукции
является истинность
высказывания
![]() ,
а индуктивное
соглашение относится
к произвольному натуральному
k,
,
а индуктивное
соглашение относится
к произвольному натуральному
k,
![]() .
.
Пример 1. Доказать, что сумма первых n нечётных чисел () равна .
►Нужно
доказать
равенство
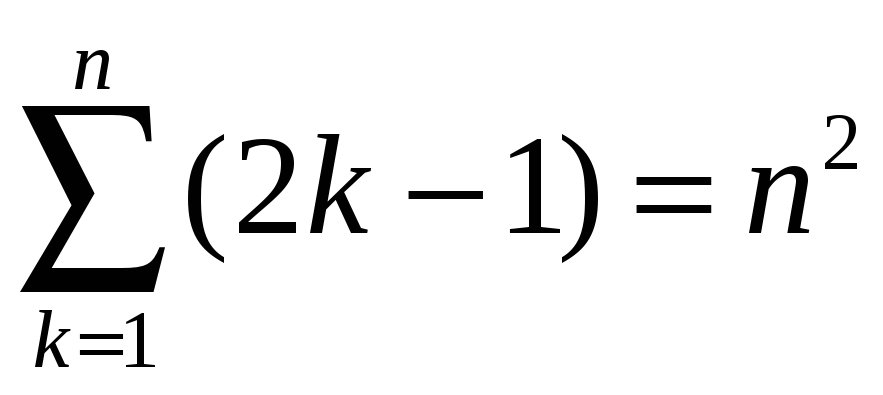 .
(1)
.
(1)
Используем метод математической индукции.
1) Формула (1) правдзицца для n = 1, бо 1 = 1.
2)
Пусть
![]() – произвольное
натуральное
число
и для
– произвольное
натуральное
число
и для
![]() равенство
(1)
истинно,
т.е.
равенство
(1)
истинно,
т.е.
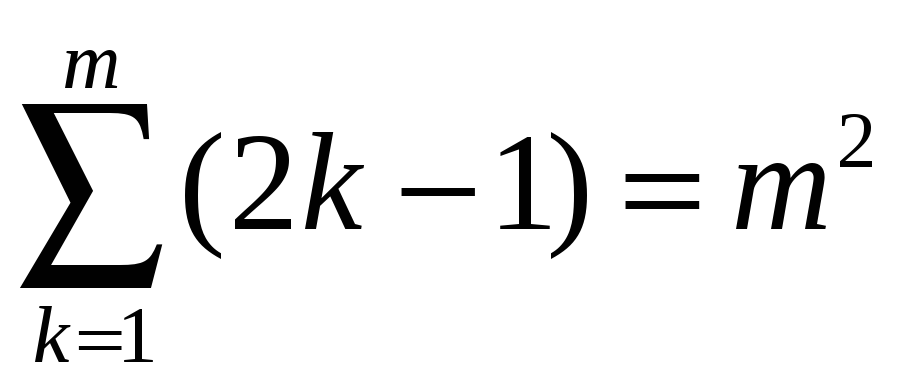 .
Докажем,
что из
этого
следует
истинность
(1) при
.
Докажем,
что из
этого
следует
истинность
(1) при
![]() .
Действительно,
.
Действительно,
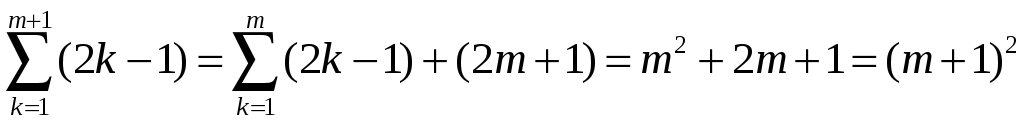 .
.
Это означает, что равенство (1) доказано для каждого натурального n. ◄
Пример 2. Найти все натуральные числа n, для которых верно неравенство
![]() . (2)
. (2)
► Утверждение,
которое можно было бы
доказвать
методом математической
индукции явно
не сформулировано.
По этой
причине
выясним закономерность
соотношения величин
![]() и
и
![]() .
Придадим последовательно
числу n
значения
.
Придадим последовательно
числу n
значения
![]() и получим
соответственно
и получим
соответственно
![]()
![]()
![]()
![]()
![]() .
Таким образом, можно
высказать
гипотезу: неравенство
(2) верное при
каждом
натуральном
.
Таким образом, можно
высказать
гипотезу: неравенство
(2) верное при
каждом
натуральном
![]() .
Докажем
это утверждение.
.
Докажем
это утверждение.
1) Истинность
базы индукции для
![]() уже доказана.
уже доказана.
2) Допустимпусцим,
что неравенство (2) верно
при произвольном
![]()
![]() ,
т.е.
,
т.е.
![]() .
(3)
.
(3)
Используя
неравенство
(3), докажем
верность неравенства
![]() .
(4)
.
(4)
Исходя
из неравенства
(3), имеем
![]() .
Если мы покажем
что
.
Если мы покажем
что
![]() ,
то это и будет
означать
верность неравенства
(4). Действительно, последнее
неравенство равносильно
неравенству
,
то это и будет
означать
верность неравенства
(4). Действительно, последнее
неравенство равносильно
неравенству
![]() ,
или
,
или
![]() ,
которое при
,
которое при
![]() является верным,
а тем самым верно
и неравенство
(4). Согласно методу
математической
индукции мы доказали,
что неравенство (2) верно
при всех
является верным,
а тем самым верно
и неравенство
(4). Согласно методу
математической
индукции мы доказали,
что неравенство (2) верно
при всех
![]() ,
а также
убедились в
его верности
при n=1.
◄
,
а также
убедились в
его верности
при n=1.
◄
