
- •Уравнение поверхности в пространстве.
- •Классификация поверхностей.
- •Плоскость в пространстве.
- •Неполные уравнения плоскости.
- •Уравнение плоскости, проходящей через три заданные точки.
- •(4) Уравнение плоскости, проходящей через 3 заданные точки.
- •Уравнение плоскости в отрезках на осях.
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.
- •Нормированное (нормальное) уравнение плоскости.
- •Пучки и связки плоскостей.
- •Прямая в пространстве.
- •Общие уравнения прямой в пространстве.
- •Канонические уравнения прямой.
- •Параметрические уравнения прямой.
- •Уравнения прямой, проходящей через две заданные точки.
- •Условие принадлежности двух прямых к одной плоскости.
- •Расстояние от точки до прямой.
- •Расстояние между двумя прямыми в пространстве.
- •Взаимное расположение прямой и плоскости в пространстве.
- •1. Пересечение прямой и плоскости.
- •Угол между прямой и плоскостью. Условия параллельности и перпендикулярности.
- •Условие параллельности прямой и плоскости.
- •Условие перпендикулярности прямой и плоскости.
- •Условие принадлежности прямой l к плоскости α.
- •Связка прямых.
Условие параллельности прямой и плоскости.
L|| ![]() n
n![]() q
q ![]() n·q=0 Al+Bm+Cn=0 (13)
n·q=0 Al+Bm+Cn=0 (13)
Условие перпендикулярности прямой и плоскости.
L![]()
![]() n||q
n||q ![]()
![]() (14)
(14)
Условие принадлежности прямой l к плоскости α.
Для того, чтобы
прямая L:
![]() принадлежала плоскости :
Ах+Ву+Сz+D=0 необходимо выполнение 2-х
условий:
принадлежала плоскости :
Ах+Ву+Сz+D=0 необходимо выполнение 2-х
условий:
-
L||;
-
Одна из точек прямой L, например точка М0(х0,у0,z0), принадлежит плоскости .
Т.о. условие принадлежности прямой плоскости:
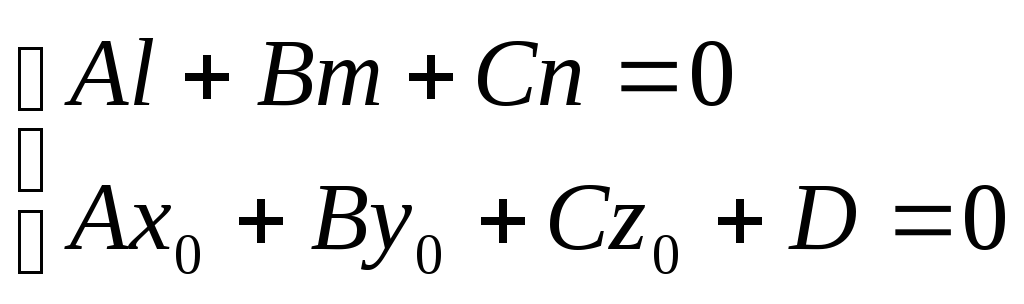 (15)
(15)
Пример. Составить
уравнение плоскости, проходящей через
точку М(4;-3;6) перпендикулярно прямой
![]() .
.
Из условия следует, что в качестве нормального вектора плоскости можно взять направляющий вектор прямой, т.е. n=q=(1;1;-2), получаем уравнение: x+y-2z+D=0. Подставляя в это уравнение координаты точки М, Найдем значение параметра D.
Связка прямых.
Совокупность всех прямых, проходящих через точку М1(x1,y1,z1), называется связкой прямых (с центром в точке М1).
Уравнения связки прямых с центром в точке М1 имеют вид:
![]() (16)
(16)
где l, m, n - произвольные числа, такие, что l2+m2+n20/
Действительно, всякая прямая, определяемая уравнениями (16), проходит через точку М1(x1,y1,z1). С другой стороны, если L – наперед заданная прямая, проходящая через точку М1(x1,y1,z1), то эта прямая однозначно определяется заданием, кроме точки М1(x1,y1,z1), направляющим вектором q={l;m;n} и потому определяются каноническими уравнениями, совпадающими с уравнениями (16).
