Неполные уравнения плоскости.

Общее уравнение прямой называется полным, если все его коэффициенты не равны 0. в противном случае уравнение называется неполным.

1. D=0 Ax+Ву+Сz=0 – плоскость, проходящая через начало координат.

Остальные случаи определяются положением нормального вектора n={А;В;С}.

2. А=0 Ву+Сz+D=0 – уравнение плоскости, параллельной оси Ох. (Т.к. нормальный вектор n={0;В;С} перпендикулярен оси Ох).

3. В=0 Ах+Сz+D=0 - уравнение плоскости, параллельной оси Оу. (Т.к. нормальный вектор n={А;0;С} перпендикулярен оси Оy).

4. С=0 Ах+Ву+D=0 - уравнение плоскости, параллельной оси Оz. (Т.к. нормальный вектор n={А;B;0} перпендикулярен оси Оz).

5. А=В=0 Сz+D=0 – z=-D/C – уравнение плоскости, параллельной плоскости Оху (т.к. эта плоскость параллельна осям Ох и Оу).

6. А=С=0 Ву+D=0 - у=-D/В- уравнение плоскости, параллельной плоскости Охz (т.к. эта плоскость параллельна осям Ох и Оz).

7. В=С=0 Ах+D=0 – x=-D/A- уравнение плоскости, параллельной плоскости Оуz (т.к. эта плоскость параллельна осям Оу и Оz).

8. A=D=0 By+Cz=0 - уравнение плоскости, проходящей через ось Ох.

9. B=D=0 Ax+Cz=0 - уравнение плоскости, проходящей через ось Оy.

10. A=B=D=0 Cz=0 (z=0) – координатная плоскость Оху. (т.к. эта плоскость параллельна Оху и проходит через начало координат).

11. А=С=D=0 By=0 (y=0) – координатная плоскость Охz. (т.к. эта плоскость параллельна Охz и проходит через начало координат).

12. B=C=D=0 Ax=0 (x=0) – координатная плоскость Оуz. (т.к. эта плоскость параллельна Оуz и проходит через начало координат).

Уравнение плоскости, проходящей через три заданные точки.

Выведем уравнение плоскости, проходящей через 3 различные точки М₁(х₁;у₁;z₁), М₂(х₂;у₂;z₂), М₃(х₃;у₃;z₃), не лежащие на одной прямой. Тогда векторы М₁М₂=(х₂-х₁;у₂-у₁;z₂-z₁) и М₁М₃=(х₃-х₁;у₃-у₁;z₃-z₁) не коллинеарны. Поэтому точка М(х,у,z) лежит в одной плоскости с точками М₁, М₂ и М₃ тогда и только тогда, когда векторы М₁М₂, М₁М₃ и М₁М=(х-х₁;у-у₁;z-z₁) - компланарны, т.е. , когда их смешанное произведение равно 0

(М₁М· М₁М₂· М₁М₃=0), т.е.

(4) Уравнение плоскости, проходящей через 3 заданные точки.

(Разложив определитель по 1-й строке и упростив получим общее уравнение плоскости: Ах+Ву+Сz+D=0).

Т.о. три точки однозначно определяют плоскость.

Уравнение плоскости в отрезках на осях.

Плоскость Π пересекает оси координат в точках М₁(а;0;0), М₂(0;b;0), M₃(0;0;c).

М(х;у;z)- переменная точка плоскости.

Векторы

М₁М=(х-а;у;z)

М₁М₂=(0-а;b;0) определяют данную плоскость

М₁М₃=(-a;0;c)

Т.е. М₁М· М₁М₂· М₁М₃=0

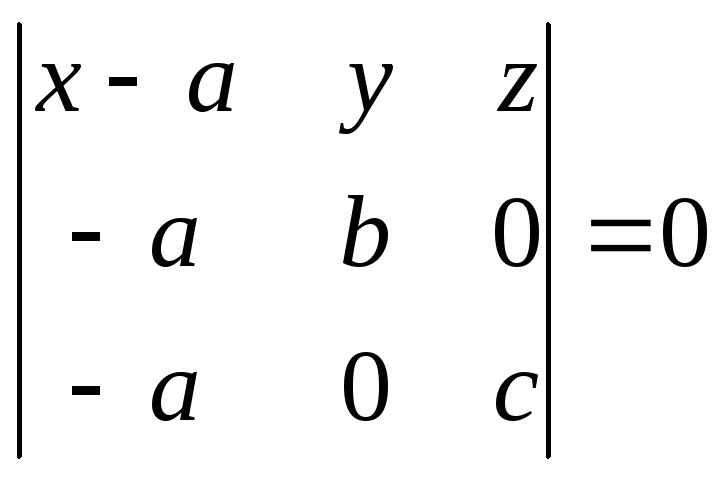Разложим по 1-й строке: (х-а)bc-y(-ac)+zab=xbc-abc+yac+zab=0

Разделим равенство на abc≠0. Получим:

(5) уравнение плоскости в отрезках на осях.

Уравнение (5) можно получить из общего уравнения плоскости, предполагая, что D≠0, разделим на D

Ax+By+Cz+D=0

Ax+By+Cz=-D

Обозначив –D/A=a, -D/B=b, -C/D=c – получим уравнение 4.

Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.

Угол φ между двумя плоскостями α₁ и α₂ измеряется плоским углом между 2 лучами, перпендикулярными прямой, по которой эти плоскости пересекаются. Любые две пересекающиеся плоскости образуют два угла, в сумме равных . Достаточно определить один из этих углов.

Пусть плоскости заданы общими уравнениями:

₁: A₁x+B₁y+C₁z+D₁=0

₂: A₂x+B₂y+C₂z+D₂=0

Нормальные векторы этих плоскостей: n₁={A₁;B₁;C₁}, n₂={A₂;B₂;C₂}.

Тогда искомый угол φ можно определить как угол между нормальными векторами n₁ и n₂, следовательно:

сosφ=, т.е. сosφ= (6)

1. Если плоскости α₁||α₂, то и нормальные векторы n₁||n₂. Следовательно, условие параллельности плоскостей: 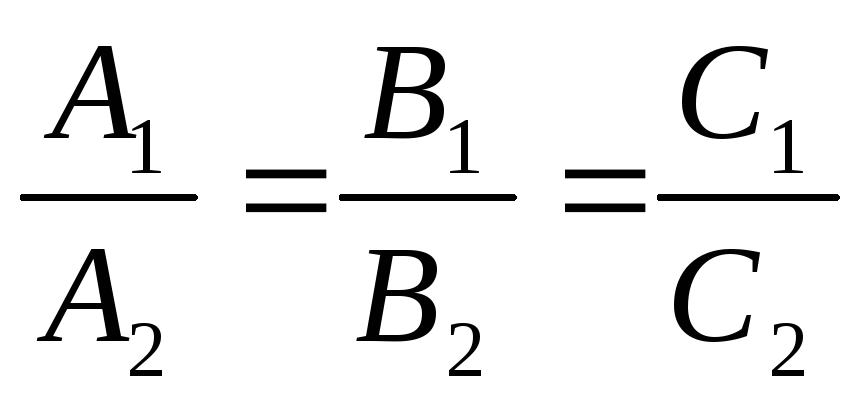(7)

При этом, если , то плоскости совпадают.

2) Если плоскости α₁α₂, то и нормальные векторы n₁n₂. Следовательно, условие перпендикулярности плоскостей: А₁А₂+В₁В₂+С₁С₂=0 (8).

Пример. Составить уравнение плоскости, проходящей через точку М(-1;3;1) параллельно плоскости 2х-3у+4z-5=0.

Т.к. α₁||α₂, то в качестве нормального вектора искомой плоскости возьмем вектор n₁=(2;-3;4). Параметр D найдем, подставив в уравнение 2х-3у+4z +D=0 координаты точки М.