
- •В.Г.Гавриленко, В.А.Яшнов
- •Введение
- •1.1. Бюджет канала связи
- •С учетом того, что мощность шума определяется выражением
- •Представим переданный сигнал в комплексной форме записи
- •Следовательно, огибающая принимаемого сигнала имеет вид
- •Здесь введен приведенный поверхностный импеданс
- •3.3.2. Отражательные формулы
- •3.3.3. Функция ослабления
- •В результате подстановки (3.120) в (3.119) получаем
- •В результате имеем
- •Тогда вместо (3.149) получаем
- •В результате из (3.170) получаем
- •3.4.4. Влияние пологих неровностей рельефа
- •В результате интерференционная формула принимает вид [11]
- •3.5. Распространение радиоволн в условиях города
- •Аналогично из (12) получаем
- •3.6. Распространение радиоволн внутри зданий и помещений
- •Таблица 3.2
- •Материал
- •Таблица 3.3
- •Относительная диэлектрическая проницаемость и тангенс потерь
- •Материал
- •Оргстекло
- •Оргстекло
- •3.6.2. Сравнение результатов измерений и расчетов

представить в виде произведения поля источника в свободном пространстве на медленно меняющуюся функцию
A |
= |
Il |
w(x, y, z, z |
)eik1r− |
, |
(3.118) |
|
4π |
|||||||
1z |
|
s |
r− |
|
|
где w(x, y, z, zs) – функция ослабления.
Вычислим функцию ослабления для вертикального диполя, расположенного вблизи плоской границы раздела двух сред. Запишем выражение для вертикальной компоненты векторного потенциала
|
|
|
|
|
Il |
|
|
|
eik1r− |
|
|
eik1r+ |
|
|
|
|
∞ ei κ1 (z+zs ) J0 (k ρ)k dk |
|
|
|
|
||||||||||||||||
|
A1z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
− 2ik1η∫ |
|
|
|
|
|
|
|
, |
|
(3.119) |
||||||
|
|
4π |
|
|
|
|
r |
− |
|
r |
+ |
|
|
κ |
1 |
(κ |
1 |
+k η) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|||||||
полученное при условии |
|
|
η |
|
<<1 . Здесь η |
– приведенный поверхностный импеданс |
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
земной поверхности, κ |
1 |
= |
|
|
|
|
|
|
k2 −k |
2 , |
k |
= k |
ε . Преобразуем интеграл, |
входящий в |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
||||||||||
выражение для векторного потенциала, используя соотношение |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −i ∫ei (κ1 +k1η)ζ dζ . |
|
|
|
|
|
|
|
(3.120) |
|||||||||||||
|
|
|
|
|
|
κ |
1 |
+ k η |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате подстановки (3.120) в (3.119) получаем |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Il |
eik1r− |
|
|
|
|
|
|
eik1r+ |
|
|
|
|
∞ ∞ ei κ1 (z+zs +ζ )ei κ1ηζ J0 (k ρ)k dk d |
ζ |
|
|||||||||||||||||||||
A1z = |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
−2k1η∫∫ |
|
|
|
|
|
|
|
|
|
|
. |
(3.121) |
||||||||||
|
|
|
|
|
|
|
|
r+ |
|
|
|
|
|
κ1 |
|
|
|
||||||||||||||||||||
|
4π r− |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Интеграл по k легко вычисляется
∞ |
i κ |
(z+z +ζ ) |
J0 (k ρ)k dk |
|
|
|
e |
ik |
|
ρ2 |
+ |
(z+z +ζ )2 |
|
|
|
|
|
||||||||||
∫ |
e |
|
1 |
|
s |
|
= −i |
|
|
1 |
|
|
|
s |
|
|
. |
|
(3.122) |
||||||||
|
|
|
|
|
|
|
|
ρ2 + (z + zs +ζ )2 |
|
||||||||||||||||||
0 |
|
|
|
|
|
|
|
κ1 |
|
|
|
|
|
|
|
|
|||||||||||
В результате имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ik r |
|
ik r |
|
|
∞ |
|
i κ1 |
|
|
|
2 |
|
2 |
|
|
|
|
||
|
|
|
|
|
Il |
|
|
|
|
e |
ηζ |
+ ρ |
|
+(z+zs +ζ ) |
|
|
|
||||||||||
A |
|
= |
e |
1 |
− + e |
1 + |
+ 2ik η |
∫ |
|
|
|
|
|
|
|
|
dζ . |
(3.123) |
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
1z |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
4π r− |
|
r+ |
|
|
|
ρ + |
(z + zs +ζ ) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим важный для радиосвязи частный случай z = zs = 0 . Тогда |
|
||||||||||||||||||||||||||
|
|
|
|
|
Il |
|
|
|
|
|
−ik r |
∞ eik1ηζ eik1 ρ2 +ζ 2 dζ eik1ρ |
|
|
|
||||||||||||
A1z |
= |
|
2 |
+ |
2ik1ηρ e |
1 |
∫ |
|
|
|
2 |
|
|
2 |
|
|
|
|
. |
|
(3.124) |
||||||
4π |
|
|
ρ |
+ζ |
|
ρ |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, выражение для функции ослабления имеет вид
∞ ik ηζ |
|
ik |
1 |
ρ2 +ζ 2 |
dζ . |
|
||
w(ρ)= 2 + 2ik1ηρ e−ik1r ∫e |
1 |
e |
|
|
|
(3.125) |
||
|
|
2 |
+ζ |
2 |
||||
0 |
|
ρ |
|
|
|
|
||
Проанализируем полученную формулу. Фаза подынтегральной функции определяется выражением
ϕ = k1 [ηζ + ρ2 +ζ 2 ]. |
(3.126) |
||||
Точка стационарной фазы ζ0 определяется из условия [13] |
|
||||
∂ϕ |
|
= 0 , |
|
(3.127) |
|
|
|
||||
∂ζ |
|
|
|||
|
ζ =ζ0 |
|
|
|
|
откуда следует, что |
|
η |
|
|
|
|
|
|
|
||
ζ0 |
|
= − |
ρ . |
(3.128) |
|
|
1 |
−η2 |
|
||
При условии η
 <<1 точка стационарной фазы лежит вне интервала интегрирования
<<1 точка стационарной фазы лежит вне интервала интегрирования
вблизи нижнего предела. Следовательно, основной вклад в интеграл дает небольшая окрестность вблизи точки ζ = 0 . Разлагая подынтегральную функцию вряд в окрест-
ности точки ζ = 0 , получаем
2 |
|
2 |
|
|
|
|
|
|
|
ζ 2 |
|
|
||
eik1 ρ |
+ζ |
≈ eik1ρ |
eik1 |
|
|
, |
|
(3.129) |
||||||
2 ρ |
|
|||||||||||||
ρ2 +ζ |
2 |
|
ρ |
|
|
|
|
|
|
|
|
|
||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ ik |
1 |
η+ |
ζ |
ζ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
w(ρ)= 2 + 2ik1η∫e |
|
2 |
ρ dζ . |
|
(3.130) |
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Введем новую переменную интегрирования u = |
|
|
k1 |
(ζ +ηρ). В результате замены по- |
||||||||||
лучаем |
|
|
|
|
|
|
|
2r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
ρη2 |
|
∞ |
|
|
|||
w(ρ)= 2 + 2i η |
2k1 ρ e−i |
1 |
|
|
|
∫eiu 2 du . |
(3.131) |
|||||||
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
k1ρ |
η |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||

Соотношение (3.131) будет исходным для анализа функции ослабления. Будем
далее полагать, что ε =1, а ε |
2 |
= ε + i |
σ |
. Здесь ε и σ – относительная диэлектриче- |
|
||||
1 |
ωε0 |
|
||
|
|
|
||
ская проницаемость и удельная проводимость почвы. Заметим, что в полученном выражении фигурирует безразмерный параметр, который принято называть численным расстоянием
ρs = |
ik 0 ρ |
. |
(3.132) |
|
|||
|
2ε2 |
|
|
При распространении радиоволн над земной поверхностью часто реализуется условие σ /ωε0 >> ε , тогда ε2 ≈ i σ /ωε0 и численное расстояние становится действительной величиной
|
|
ρs = |
k2 |
ρ |
. |
(3.133) |
|
|
0 |
|
|||
|
|
2σZ0 |
||||
|
|
|
|
|
||
Здесь Z = µ0 |
– характеристический импеданс свободного пространства. |
|
||||
0 |
ε0 |
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим поведение функции ослабления при малых численных расстояниях, т.е. при условии ρs <<1. В этом случае нижний предел интегрирования в выражении (3.131) мал и приближенно можно считать, что
∞ |
|
∞ |
1 |
|
|
∫eiu 2 |
du ≈ ∫eiu 2 du = |
i π . |
(3.134) |
||
k1ρ |
η |
0 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Тогда выражение для функции ослабления принимает вид
w(ρ)= 2(1 +i πρs ). |
(3.135) |
При малых численных расстояниях ( ρs <<1) w(ρ)≈ 2 , т.е. амплитуда поля убывает с
расстоянием по закону 1 ρ , так же, как в свободном пространстве. Поле вертикаль-
ρ , так же, как в свободном пространстве. Поле вертикаль-
ного электрического диполя вблизи земной поверхности при этом удваивается по сравнению со случаем свободного пространства. Таким образом, при малых численных расстояниях земная поверхность эквивалентна идеально проводящему полупространству.
При больших численных расстояниях ( ρs >>1) входящий в выражение для функции ослабления интеграл удобно взять по частям. В результате получаем
∞ |
1 |
|
|
|
|
1 |
|
|
|
∫exp(iu 2 )du = − |
eia |
2 |
|
|
|
||||
|
|
1 |
+ |
|
|
+... , |
(3.136) |
||
2ia |
|
2ia |
2 |
||||||
a |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
где a = |
k0 ρ . Используя (3.136), перепишем выражение для функции ослабления |
|
2ε2 |

w ≈ 2 |
− 2 ρ |
s |
1 |
|
1 + |
1 |
|
, |
(3.137) |
|
|
|
|
ρs |
|
|
|
|
|
|
|
|
|
|
|
|
|
2ρs |
|
|
||
Окончательно получаем |
|
|
|
|
|
|
|
|
|
|
|
w ≈ − |
1 |
. |
|
|
|
|
|
(3.138) |
|
|
|
|
|
|
|
|
||||
|
|
|
ρs |
|
|
|
|
|
|
|
Выражение (3.138) для функции ослабления справедливо при больших значениях численного расстояния, т.е. при условии
ρs |
|
>>1. |
(3.139) |
|
Таким образом, результаты анализа показывают, что при больших численных расстояниях поле убывает по закону 1/ ρ2 , т.е. гораздо быстрее, чем в свободном про-
странстве.
Принципиально важным является вопрос о скорости распространения радиоволн вдоль земной поверхности. Отметим, что в общем случае функция ослабления является комплексной величиной и может быть представлена в виде
w(ρ)= |
|
w(ρ) |
|
exp(i α(ρ)), |
(3.140) |
|
|
где α(ρ) – аргумент функции ослабления. С учетом (3.140) фаза волны, распространяющейся вдоль земной поверхности, может быть записана в виде
ϕ(ρ,t )= k0 ρ −ωt +α(ρ). |
(3.141) |
Следовательно, фазовая скорость определяется следующим выражением:
v = dρ |
= − |
∂ϕ / ∂t |
= |
ω |
|
∂ϕ / ∂ρ |
k0 + dα dρ |
||||
dt |
|
|
При больших значениях численного расстояния
w = − |
1 |
= |
2i ε2 |
, |
||
ρs |
|
|||||
|
|
|
k0 ρ |
|||
следовательно, |
|
|
|
|
|
|
|
π |
|
|
|
σω |
|
α = |
|
|
|
|
|
|
2 |
+ arctg |
εε0 |
||||
|
|
|
|
|||
= |
|
|
c |
|
|
. |
|
1 + |
1 |
|
dα |
|
|||
|
|
|
|||||
|
|
|
k0 |
dρ |
|||
.
(3.142)
(3.143)
(3.144)
Из (3.144) следует, что α не зависит от расстояния ρ . Это означает, что при больших
численных расстояниях фазовая скорость не зависит от электрических свойств земной поверхности и равна скорости света в вакууме.
3.3.4. Потери при распространении радиоволн над плоской поверхностью Земли
При распространении радиоволн в пригородной зоне на свободных от строений пространствах для расчета радиотрасс могут быть использованы так называемые отражательные формулы, согласно которым электромагнитное поле в точке приема может быть представлено в виде суммы прямой волны и волны, отраженной от поверхности Земли,
|
|
E = E |
0 |
1 + R2 |
+ 2R cos(2kz cosϑ +ψ ), |
|
(3.145) |
|||||||
где |
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
E0 |
= |
|
90PT |
sinϑ , |
|
R = |
ε cosϑ − |
ε − cos2 ϑ |
, |
(3.146) |
||
|
|
|
d |
|
ε cosϑ + |
ε − cos2 ϑ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
PT – излучаемая мощность, |
d – расстояние между передающей и приемной антенна- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ми, измеряемое вдоль поверхности |
|||
|
|
|
|
|
|
|
|
|
|
|
Земли, |
R – коэффициент отраже- |
||
|
|
|
|
|
|
|
|
|
|
|
ния Френеля плоской волны от |
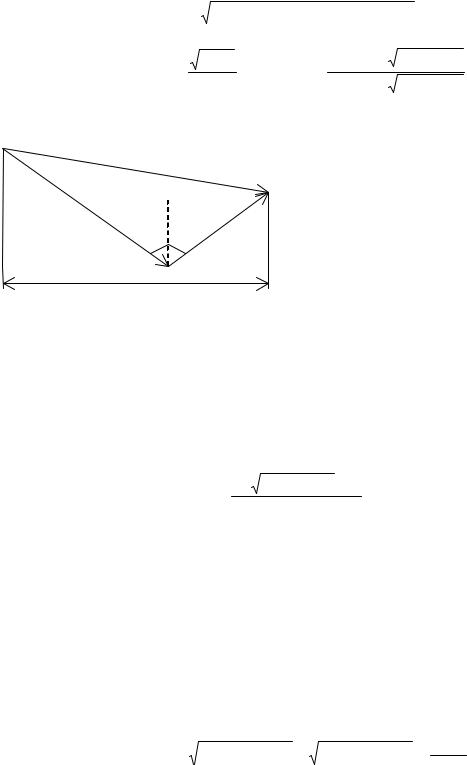
|||
|
z1 |
|
|
|
|
|
|
|
|
|
земной |
поверхности, ε |
– ком- |
|
|
ϑ |
ϑ |
|
|
|
|
z2 |
плексная диэлектрическая |
прони- |
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
цаемость Земли, ϑ – угол падения |
||||||
|
|
|
|
|
|
|
|
|
|
|
волны (рис. 3.10). На практике |
|||
|
|
|
|
|
|
|
|
|
|
|
часто высоты подъема передаю- |
|||
|
|
d |
|
|
|
|
|
|
|
|
щей и |
приемной антенн |
удовле- |
|
|
|
Рис. 3.10 |
|
|
|
|
|
|
|
творяют соотношению |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
4z1z2 |
|
<< d , |
|
|
(3.147) |
||
|
|
|
|
|
|
|
λ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда с учетом направленных свойств антенн вместо (3.145) имеем |
|
|
||||||||||||
|
|
|
|
|
E = 4π |
60PTGTGR z1z2 . |
|
|
(3.148) |
|||||
|
|
|
|
|
|
|
|
|
d2 |
|
|
|
|
|
Выражение (3.148) известно как квадратичная формула Введенского [14].
Для оценки принимаемой мощности можно воспользоваться следующими соотношениями. Мощность на входе приемной антенны, расположенной вблизи земной поверхности, может быть представлена в виде
P |
= P |
|
1 − exp(ik ∆r ) |
|
2 , |
(3.149) |
|
|
|||||
r |
r 0 |
|
|
|
|
|
где ∆r – разность хода между прямой и отраженной от земной поверхности волнами. Если высоты расположения антенн удовлетворяют условию (3.147), то
∆r = |
(z |
+ z )2 |
+ d2 |
− |
(z |
− z )2 |
+ d2 |
≈ 2z1z2 . |
(3.150) |
|
1 |
2 |
|
|
1 |
2 |
|
d |
|
|
|
|
|
|
|
|
|
|
