
- •В.Г.Гавриленко, В.А.Яшнов
- •Введение
- •1.1. Бюджет канала связи
- •С учетом того, что мощность шума определяется выражением
- •Представим переданный сигнал в комплексной форме записи
- •Следовательно, огибающая принимаемого сигнала имеет вид
- •Здесь введен приведенный поверхностный импеданс
- •3.3.2. Отражательные формулы
- •3.3.3. Функция ослабления
- •В результате подстановки (3.120) в (3.119) получаем
- •В результате имеем
- •Тогда вместо (3.149) получаем
- •В результате из (3.170) получаем
- •3.4.4. Влияние пологих неровностей рельефа
- •В результате интерференционная формула принимает вид [11]
- •3.5. Распространение радиоволн в условиях города
- •Аналогично из (12) получаем
- •3.6. Распространение радиоволн внутри зданий и помещений
- •Таблица 3.2
- •Материал
- •Таблица 3.3
- •Относительная диэлектрическая проницаемость и тангенс потерь
- •Материал
- •Оргстекло
- •Оргстекло
- •3.6.2. Сравнение результатов измерений и расчетов
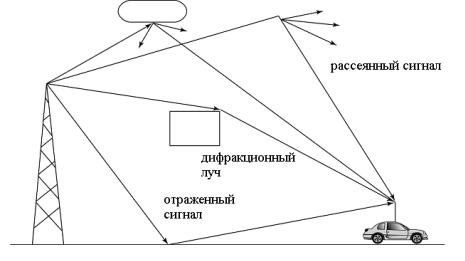
Рис. 1.6
Представим переданный сигнал в комплексной форме записи
s(t )= Re[g(t)exp(iωt)], |
(1.41) |
где Re[…] – знак действительной части выражения […], ω – несущая частота сигнала, g(t) – комплексная огибающая сигнала s(t). Огибающую удобно представить в виде
g(t)= |
|
g(t) |
|
exp(iϕ(t))= R(t)exp(iϕ(t)) |
(1.42) |
|
|
где R(t) – модуль огибающей, а ϕ(t) – ее фаза. Для сигнала с частотной или фазовой модуляцией R(t) будет постоянной величиной.
В процессе распространения сигнала на трассе происходит изменение огибающей сигнала, которая в этом случае может быть записана в следующем виде:
~ |
(t)=α(t)e |
−iθ (t ) |
g(t), |
(1.43) |
g |
|
где множитель α(t)e−iθ (t ) характеризует затухание сигнала на трассе. Амплитуда
модифицированной огибающей (1.43) может быть представлена в виде произведения трех сомножителей
α(t)R(t)= m(t) r0 (t) R(t). |
(1.44) |
Здесь m(t) – множитель, описывающий крупномасштабное замирание огибающей, r0 (t) – мелкомасштабное замирание. Иногда m(t) называют локальным
средним или логарифмически нормальным замиранием, поскольку его значения можно статистически описывать с помощью логарифмически нормальной функции распределения вероятностей. При этом выраженное в децибелах значение m(t) будет описываться гауссовой функцией распределения вероятностей.
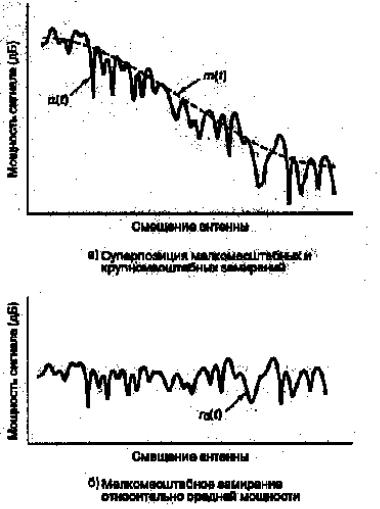
Множитель r0 (t) описывает релеевское замирание. На рис. 1.7 схематически по-
казаны крупномасштабные и мелкомасштабные замирания сигнала. Предполагается, что передается немодулированная волна, т.е. в любой момент времени R(t )=1 . Характерное смещение антенны, соответствующее мелкомасштабным
замираниям, примерно равно половине длины волны. Локальное среднее m(t) можно оценить путем усреднения огибающей сигнала по 10-30 длинам волн. Логарифмически нормально распределенное замирание является относительно медленно меняющейся функцией местоположения приемной антенны. Для мобильного приемника замирания в пространстве эквивалентны временным вариациям сигнала.
Крупномасштабные замирания
Для систем мобильной связи Окумурой [7] было проведено большое число измерений затухания на трассах различной протяженности для различных высот передающей и приемной антенн. На основе результатов измерений Хата [8] предложил эмпирические формулы, позволяющие рассчитать затухание сигнала. Результаты измерений и теоретических расчетов показывают, что среднее значение потерь растет с ростом расстояния d между передающей и приемной антеннами пропорционально некоторой степени расстояния
|
|
d |
n |
|
|
|
|
, |
|
|
|
|||
Lp (d ) |
|
|
||
|
d0 |
|
|
|
(1.45)
где d0 – некоторое
|
начальное |
расстоя- |
|
|
ние, |
соответствую- |
|
|
щее некоторой точ- |
||
|
ке в |
дальней зоне |
|
|
передающей антен- |
||
|
ны. Обычно d0 вы- |
||
|
бирается |
равным |
|
Рис. 1.7 |
1 км |
для |
макросот, |
|
100 м – для микро- |
||
|
|||
сот и 1 м – для пикосот. Показатель степени n в свободном пространстве равен 2. При распространении вдоль улиц или в коридорах зданий, где наблюдается волноводный

механизм распространения радиоволн n может быть меньше 2. При наличии препятствий n больше двух. Обычно потери выражаются в децибелах
|
|
d |
|
|
|
|
|
|
, |
(1.46) |
|
|
|
||||
Lp (d)= Ls(d0 )+10nlg d |
|
||||
|
|
0 |
|
|
|
где Ls(d0 ) – затухание на трассе прямой видимости длиной d0 .
График зависимости Lp (d) в логарифмическом масштабе представляет
Рис 1 8
собой прямую линию, тангенс угла наклона которой равен 10n . На рис. 1.8 показаны потери в зависимости от расстояния, измеренные в нескольких городах Германии. Здесь потери измерялись относительного начального расстояния d0 =100 м. Из рис. 1.8 видно, что разброс величины потерь на различных
трассах может быть значительным. Измерения показывают, что потери являются случайной величиной, имеющей логарифмически нормальное распределение в окрестности среднего значения. Таким образом, потери можно представить в следующем виде
|
d |
|
|
|
|
|
|
+ Xσ , |
(1.47) |
||
|
|||||
Lp (d)= Ls(d0 )+10nlg d |
|
||||
|
0 |
|
|
|
|
где Xσ – случайная гауссова величина с нулевым средним и среднеквадратичным отклонением σ . Значение Xσ зависит от местоположения приемной антенны и расстояния между приемником и передатчиком. Обычные значения Xσ
– это 6-10 дБ, в ряде случаев и больше.
Таким образом, для статистического описания потерь вследствие крупномасштабного замирания при расположении корреспондирующих пунктов на определенном расстоянии необходимы следующие параметры: 1) эталонное расстояние d0 , 2) показатель степени n и 3) среднеквадратичное отклонение
Xσ .
Мелкомасштабное замирание
Предположим, что перемещение приемной антенны происходит в ограниченной области пространства так, что влияние крупномасштабного замирания можно не учитывать, т.е. множитель m(t ) в (4) равен единице. Пусть сиг-
нал в точку приема приходит различными путями в результате отражения от многих объектов, расположенных вдоль радиотрассы (многолучевое распространение). С каждой траекторией распространения сигнала связано свое время задержки τn (t ) и свой амплитудный множитель αn (t ). Принимаемый сигнал в
этом случае можно записать в виде
r (t )= ∑αn (t )s[t −τn (t )]. |
(1.48) |
|
n |
|
|
|
Подставляя (1.41) в (1.48), получаем |
|
|
|
|
|
|
|
|
|
|
i ω[t −τn (t )] |
= |
||
r (t )= Re |
∑αn (t )g[t −τn (t )] e |
|
||
|
n |
|
|
|
|
|
|
|
−i ωτn (t ) |
|
|
= |
|
|
i ωt |
|||
Re |
∑αn (t )e |
|
g[t −τn (t )] e |
|
||
|
|
|
n |
|
|
|
Следовательно, огибающая принимаемого сигнала имеет вид
z(t )= ∑αn (t )e−i ωτn (t ) g[t −τn (t )].
(1.49)
(1.50)
n
Рассмотрим передачу немодулированного сигнала (несущей) на частоте ω . В этом случае g(t )=1 и из (1.50) получаем
z(t )= ∑αn (t )e−i ωτn (t ) =∑αn (t )e−i θn (t ) , |
(1.51) |
|
n |
n |
|
где θn (t )=ωτn (t ). Сигнал (11) состоит из суммы переменных во времени векторов, имеющих амплитуду αn (t ) и фазу θn (t ). Заметим, что фаза сигнала изменя-

ется на 2π радиан при изменении задержки τn на величину 2π /ω =1/ f . Например, при значении несущей частоты сигнала f = 900 Мгц задержка состав-
ляет всего 1,1 нс. Такое изменение времени задержки соответствует изменению длины пути распространения радиоволн в свободном пространстве на 33 см.
Выражение (1.51) можно записать в более компактном виде
z(t )=α(t )e−i θ (t ). |
(1.52) |
Здесь α(t ) – результирующая амплитуда, а θ(t ) |
– результирующая фаза. На |
рис. 1.9 показан пример интерференции двух сигналов (прямого и отраженного), приводящей к мелкомасштабным замираниям. Отраженный сигнал имеет
Потеря амплитуды
|
|
|
|
|
|
|
|
|
|
Отраженный |
|
|
|
|
|
|
|
|
|
сигнал |
|
|
|
yn |
|
|
|
|
|
|
|
|
|
|
Желательный |
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
сигнал |
|
|
|
xn |
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.9

меньшую по сравнению с прямым сигналом амплитуду и фазовый сдвиг, связанный с увеличением пути распространения. Отраженные сигналы можно описать с помощью ортогональных компонентов xn (t ) и yn (t ), где
xn (t )+ iy n (t )=αn (t )e−i θn (t ) . |
(1.53) |
Если количество таких компонентов велико и ни один из них не преобладает (такая ситуация имеет место при отсутствии прямого сигнала), то в фиксированный момент времени переменные xr (t ) и yr (t ), являющиеся результатом
суммирования всех xn (t ) и yn (t ), соответственно, будут иметь гауссову функ-
цию распределения вероятностей. Эти ортогональные компоненты дают мелкомасштабное замирание r0 , определенное в (1.54). При немодулированной несу-
щей r0 является модулем z(t )
r (t )= |
x 2 |
(t )+ y2 |
(t ). |
(1.54) |
0 |
r |
r |
|
|
Если принимаемый сигнал является суммой множества отраженных сигналов и значительного по амплитуде прямого сигнала (при наличии прямой видимости между передающей и приемной антеннами), то амплитуда огибающей в этом случае имеет райсовскую функцию распределения плотности вероятности
|
r0 |
|
(r02 + A2 ) |
r0 A |
|
|
|||||||
p(r )= |
|
|
|
exp − |
|
|
I 0 |
|
|
2 |
для |
r0 ≥ 0, A ≥ 0 . |
(1.55) |
|
2 |
2σ |
2 |
σ |
|||||||||
0 |
σ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
для других r0 , A |
|
||
|
|
|
|
|
|
|
|
|
|
||||
В этом случае замирания называют райсовскими. Здесь I 0 (x ) – модифи-
цированная функция Бесселя первого рода нулевого порядка.
При движении приемника величина r0 меняется со временем, но в любой
фиксированный момент времени – это случайная величина, являющаяся положительным действительным числом. Поэтому, описывая функцию плотности
вероятности, зависимость от времени можно опустить. При этом параметр σ 2 имеет смысл средней мощности многолучевого сигнала, A – так называемый зеркальный компонент. Распределение Райса часто записывают через параметр K , определяемый как отношение мощности зеркального компонента к мощности многолучевого сигнала
K = |
A2 |
. |
(1.56) |
|
2σ 2 |
||||
|
|
|
При уменьшении зеркального компонента до нуля распределение Райса стремится к распределению Релея
|
r |
|
exp |
|
− |
r 2 |
|
|
I |
|
r A |
для |
r ≥ 0 |
|
|
|||
p(r )= |
|
0 |
|
0 |
|
|
0 |
0 |
|
|
. |
(1.57) |
||||||
|
|
2 |
2 |
|||||||||||||||
σ |
2 |
|
|
2σ |
|
σ |
|
|
0 |
|||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
для других |
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Релеевский замирающий компонент иногда называют случайным, рассеянным или диффузным. Таким образом, распределение Релея описывает канал в отсутствии зеркального компонента.
Мелкомасштабное замирание проявляется двумя способами: (1) путем расширения цифровых импульсов сигнала и (2) посредством переменного во времени поведения канала, вызванного движением мобильной станции. Каждый из возможных механизмов замираний можно рассматривать в двух областях – временной и частотной. Во временной области расширение сигнала, связанное с многолучевостью, характеризуется временем задержки, а в частотной области – полосой когерентности. Подобным образом нестационарный механизм во временной области будет характеризоваться временем когерентности сигнала, а в частотной области – скоростью замирания или доплеровским расширением.
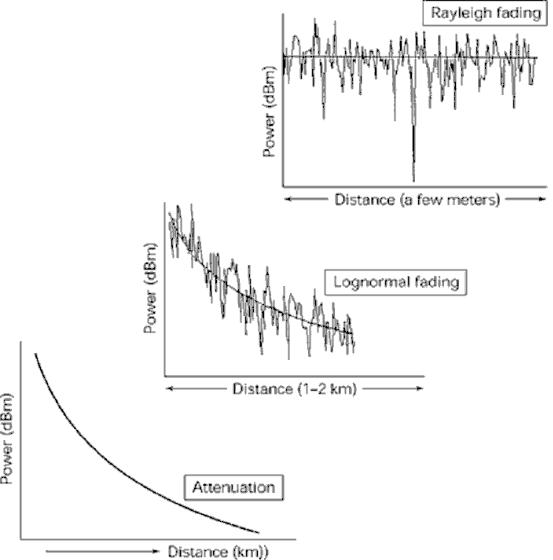
На рис. 1.10 приведены характерные зависимости амплитуды принимаемого сигнала при наличии замираний.
Рис. 1.10
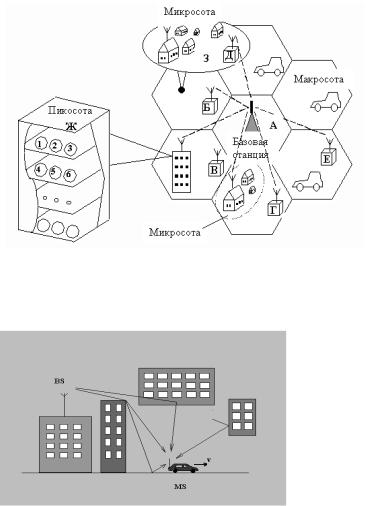
2. Основные особенности распространения радиоволн в системах мобильной связи
Типовая модель системы мобильной связи включает в себя одну или несколько поднятых антенн базовой станции, относительно короткий участок радиотрассы прямой видимости (LOS), несколько радиотрасс с переотражениями, т.е. трасс непрямой видимости (NLOS), а также несколько антенн подвижных станций. Структура такой системы показана на
рис. 2.1.
Размеры макросот, как правило, больше километра. Мощность передающей станции превышает 10 Вт. Коэффициент усиления пере-
Рис. 2.1 |
дающей антенны – 10- |
|
20 дБ. |
Макросоты |
|
плохо изолированы одна от другой. Распространение сигнала внутри макросоты характеризуется большим временным рассеянием. В пределах макросоты находится большое число рассеивателей, распространение имеет многолучевой характер.
Микросоты имеют размеры 0,1-1 км. Типичная мощность передатчика базовой станции более 1 Вт. Используются передающие антенны с коэффициентом усиле-
Рис. 2.2 ния 5-10 дБ. Микросоты хорошо изолированы одна от другой. Для сигналов, распространяющихся внутри микросоты характерны небольшие временные
задержки. Присутствуют как открытые, так и закрытые трассы. При связи с подвижным объектом наблюдаются значительные замирания сигнала (до 20-30 дБ), связанные с изменением условий распространения радиоволн.
Пикосоты (офисы, магазины, железнодорожные станции, аэропорты) имеют размеры 10-200 м. Антенна базовой станции располагается либо вне здания, либо внутри него. В последнем случае часто используются распределенные антенные системы. Коэффициенты усиления антенн около 2 дБ. Для пикосот характерно очень малые времена задержки сигнала.
В большинстве случаев радиосвязь ведется в отсутствие прямой видимости. В этих условиях может существовать более одного пути распространения радиоволн между базовой и мобильной станциями. Такое распространение называется многолучевым. Радиоволны приходят в точку приема в результате многократного отражения от зданий и других объектов. Трасса распространения

радиоволн, как правило, нестационарна, что связано либо с перемещением мобильной станции, либо с перемещением других подвижных объектов, например, автомобилей. Распространение радиоволн в подобных условиях характеризуется следующими основными эффектами: замираниями, связанными с многолучевостью; затенением (или экранированием); временным рассеянием; доплеровским рассеянием и потерями при распространении. Рис. 2.2 иллюстрирует многолучевой характер распространения радиоволн между базовой и мобильной станциями. В результате многократного отражения радиоволн от различных объектов при работе передатчика в режиме непрерывного излучения создается сложная интерференционная картина, приводящая к замираниям принимаемого сигнала. Пример таких замираний (федингов), связанных с движением приемника приведен на рис. 2.3.
При работе передатчика в импульсном режиме многолучевое распро-
|
странение может приводить к тому, |
|
|
что в точке приема наблюдаются сиг- |
|
|
налы с различными временными за- |
|
|
держками. Накладываясь один на дру- |
|
|
гой, они могут приводить к заметному |
|
|
искажению сигнала |
(межсимвольной |
|
интерференции). Это явление называ- |
|
|
ется временным рассеянием сигнала. |
|
|
Основными |
характеристиками |
|
временного рассеяния являются верх- |
|
|
няя граница временного рассеяния и |
|
|
среднеквадратичное значение времен- |
|
Рис. 2.3 |
ного рассеяния (рис. 2.4 и 2.5). |
|
|
|
|
Рис. 2.4 |
|
Рис. 2.5 |
|
|
|
|
|
|
Замирания на трассе можно разделить на долговременные (усредненные) и кратковременные (быстрые). Если усреднить быстрые замирания, связанные с многолучевостью, остается неселективное затенение. Причиной этого явления являются особенности рельефа местности вдоль трассы распространения радиоволн.
В следующем разделе будут рассмотрены некоторые модели, используемые для описания особенностей распространения радиоволн в системах мобильной связи.

3.Модели, используемые для описания распространения радиоволн
3.1.Основы теории распространения радиоволн в свободном пространстве и при наличии препятствий
3.1.1. Решение уравнения Гельмгольца для векторного потенциала в свободном пространстве
При изучении излучения и распространения электромагнитных волн широко используются векторные и скалярные потенциалы электромагнитного по-
ля. Известно, что векторный потенциал электрического типа A для гармонических полей удовлетворяет уравнению Гельмгольца [9]
∆A + k2 A = −j , |
(3.1) |
где k = ω εε0 µµ0 – волновое число, j – плотность электрического тока в ис-
точнике. В однородном безграничном пространстве с заданным распределением токов в ограниченной области V строгое решение уравнения (3.1) можно записать в виде
|
1 |
∫ j |
eikr |
|
1 |
|
|
∂ϕ |
|
∂A |
|
A = |
|
|
dV − |
|
|
|
|
−ϕ |
|
(3.2) |
|
|
|
|
∫ A |
|
dS , |
||||||
|
4π |
V |
r |
|
4π |
S |
|
∂n |
|
∂n |
|
где n – внешняя нормаль к поверхности |
S , |
ϕ – вспомогательная функция, |
|||||||||
удовлетворяющая однородному уравнению Гельмгольца. В качестве такой функции можно взять
ϕ = |
eikr |
, |
(3.3) |
|
r |
||||
|
|
|
где r – расстояние от текущей точки интегрирования до точки наблюдения. Если наряду с заданным в области V распределением j заданы значе-
ния A и ∂A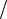 ∂n на поверхности S , то (3.3) представляет собой решение урав-
∂n на поверхности S , то (3.3) представляет собой решение урав-
нения (3.1). В случае свободного пространства оказывается возможным выбрать поверхность S таким образом, чтобы поверхностный интеграл в (3.2) был равен нулю. Следовательно, электромагнитное поле заданных в токов в свободном пространстве может быть представлено в виде
A = |
1 |
∫ j |
eikr |
dV . |
(3.4) |
|
4π |
r |
|||||
|
V |
|
|
В частности, если источником служит элементарный электрический вибратор, расположенный в начале декартовой системы координат и ориентированный
вдоль оси z , то j = Il δ (x)δ (y)δ (z)ez , где Il – токовый момент. Тогда
A = |
Il |
|
eikr |
e . |
(3.5) |
|
|
||||
|
4π |
|
r |
z |
|
|
|
|
|
Как видно из (3.5), поле элементарного электрического вибратора представляет собой расходящуюся сферическую волну. Следовательно, выражение (3.4) для произвольного излучателя на больших расстояниях также представляет собой сферическую волну.
3.1.2. Математическая формулировка принципа Гюйгенса-Френеля.
Рассмотрим замкнутую область пространства, ограниченную двумя замкнутыми поверхностями S и S1 , внутри которой находится точка наблюдения. Предпо-
ложим, что источники поля расположены внутри области V0 , ограниченной поверхностью S . Применяя формулу (3.2), получаем [10]
|
1 |
|
|
∂ϕ |
|
∂A |
1 |
∫ |
|
∂ϕ |
|
∂A |
|
A = − |
|
|
|
|
−ϕ |
|
|
|
|
−ϕ |
|
(3.6) |
|
4π |
∫ A |
∂n |
dS − |
4π |
A |
∂n |
dS . |
||||||
|
S |
|
|
∂n |
S1 |
|
|
∂n |
|
||||
Поскольку вне области, ограниченной поверхностью S1 , токов нет, то поверх- |
|||||||||||||
ностный интеграл по S1 |
равен нулю. С другой стороны, токи вне поверхности |
||||||||||||
S вообще отсутствуют. Следовательно, поле в точке наблюдения может быть определено двояким образом:
|
|
|
1 |
∫j |
e |
ikr |
dV , |
|
|||
|
|
|
|
||||||||
|
|
|
|
|
|||||||
|
|
4π |
|
r |
|
||||||
|
|
|
V0 |
|
|
|
|
(3.7) |
|||
A = |
1 |
|
|
|
|
∂ϕ |
|
|
|
||
|
|
∫ |
|
|
−ϕ |
∂A |
|
||||
− |
4π |
A |
∂n |
dS. |
|
||||||
|
S |
|
|
|
|
∂n |
|
||||
Здесь S – произвольная замкнутая поверхность, охватывающая источники поля, V0 – объем, занимаемый источниками.
Таким образом, в соответствии с выражениями (3.7) поле в точке наблюдения может быть определено как поле первичных излучателей непосредственно, либо может рассматриваться как поле вторичных источников, непрерывно распределенных по замкнутой поверхности, охватывающей первичные источники. Понятие вторичных источников было впервые введено Гюйгенсом во второй половине XVII века. В соответствии с принципом Гюйгенса каждая точка волнового фронта может рассматриваться как источник вторичных сферических волн. В начале XIX века Френель дополнил принцип Гюйгенса, сделав его пригодным для объяснения дифракционных эффектов. Формула (3.7) , по существу, является математической формулировкой принципа Гюйгенса-Френеля.
3.1.3. Зоны Френеля
Рассмотрим пример применения формулы Кирхгофа (3.7). Пусть поверхность S состоит из двух частей – плоскости S0 и полусферы S∞ радиуса r∞ с

центром на плоскости S0 (см. рис. 3.1). Предположим, что в точке О располо-
жен точечный излучатель – элементарный диполь. В соответствии с (3.7) поле в точке наблюдения А можно записать в виде
|
1 |
∫ |
|
∂ϕ |
|
A = − |
|
|
|
−ϕ |
|
|
|
||||
4π |
A |
∂n |
|||
|
S0 |
|
|
Вычислим интеграл по полусфере
Рис. 3.1
∂∂An ≈ ik
∂A |
1 |
|
∂ϕ |
|
|
|
|
|
|
||
dS − |
4π |
∫ A |
∂n |
∂n |
S∞ |
S∞ . Заметим, что
,
Iπl erikr cos(n, eρ ). 4
|
∂A |
|
−ϕ |
|
(3.8) |
dS . |
||
|
∂n |
|
∂∂ϕn = ∂∂ϕr cos(n, er ),
(3.9)
∂∂An = ∂∂Ar cos(n, eρ ).
(3.10)
Здесь er и eρ – единичные векторы. Если радиус полусферы r∞ достаточно велик, так что выполняются
условия |
kr >>1 и |
||
kρ >>1 , то |
|
||
∂ϕ ≈ ik |
eikr |
cos(n, e ) |
|
|
|||
∂n |
r |
r |
|
(3.11) |
|||
|
|
||
|
|
(3.12) |
|
При устремлении радиуса полусферы r∞ к бесконечности интеграл по полусфе-
ре стремится к нулю.
Отметим, что при наличии внутри рассматриваемой области нескольких первичных источников интеграл по поверхности полусферы бесконечно большого радиуса также стремился к нулю.
Таким образом, в однородной безграничной среде поле может быть выражено через поверхностный интеграл по безграничной плоскости, расположенной между излучателем и точкой наблюдения
|
1 |
∫ |
|
∂ϕ |
|
∂A |
|
A = − |
|
|
|
−ϕ |
|
(3.13) |
|
|
|
||||||
|
A |
|
dS . |
||||
|
4π |
S0 |
|
∂n |
|
∂n |
|
Известно, что на этой плоскости можно выделить наиболее существенную область интегрирования. Воспользуемся тем, что существует некоторая свобода в выборе функции ϕ . Функция ϕ является решением уравнения Гельмгольца,
соответствующим расходящимся волнам. Можно выбрать ϕ так, чтобы на поверхности S0 выполнялось одно из двух условий: ϕ = 0 или ∂ϕ ∂n = 0 . В качестве таких функций можно выбрать следующие:
∂n = 0 . В качестве таких функций можно выбрать следующие:
ϕ = eikr1 |
− eikr 2 |
, |
(3.14) |
|
r |
r |
2 |
|
|
1 |
|
|
|
|
ϕ = eikr1 |
+ eikr 2 . |
(3.15) |
||
r |
r |
2 |
|
|
1 |
|
|
|
|
Здесь r1 – расстояние от точки наблюдения до произвольной точки в области наблюдения, а r2 – расстояние от зеркального изображения точки наблюдения в плоскости S0 до той же точки. Тогда используя (3.14) из (3.13) получаем
|
1 |
∫ |
|
∂ |
|
ikr |
|
|
|
|
|
|
|
|
|
||||
A = − |
|
A |
|
e |
|
dS . |
(3.16) |
||
2π S |
|
|
|
||||||
|
|
∂n |
r |
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
Пользуясь формулой (3.16), можно вычислить поле в точке наблюдения в виде интеграла по вторичным источникам, расположенным в безграничной плоскости, которую удобно расположить перпендикулярно прямой, соединяющей первичный источник и точку наблюдения. Взяв в качестве первичного источника элементарный электрический диполь, получаем
A = |
iI l |
|
eik (r +ρ ) |
cos(n, e )dS . |
(3.17) |
4πλ S∫ |
|
||||
|
rρ |
r |
|
||
|
|
|
|||
0 |
|
|
|
||
Анализ интеграла (3.17) позволяет установить наличие области, существенной при распространении радиоволн. Этот анализ удобно проводить с помощью построения зон Френеля. Разделим плоскость S0 на области, границы которых
определяются следующими условиями
ρ |
1 |
+ r − (ρ |
0 |
+ r |
0 |
)= λ |
, |
|
|
|
1 |
|
2 |
|
|
|
|||
|
|
|
|
|
|
λ |
|
|
|
ρ2 + r2 − (ρ0 |
+ r0 )= 2 |
, |
(3.18) |
||||||
|
|
|
|
|
|
|
2 |
|
|
… |
|
|
|
|
|
|
|
|
|
ρn + rn − (ρ0 |
+ r0 )= n |
λ . |
|
||||||
|
|
|
|
|
|
|
2 |
|
|
Согласно этим равенствам вторичные источники, расположенные на границах двух соседних зон, излучают волны, приходящие в точку наблюдения в проти-
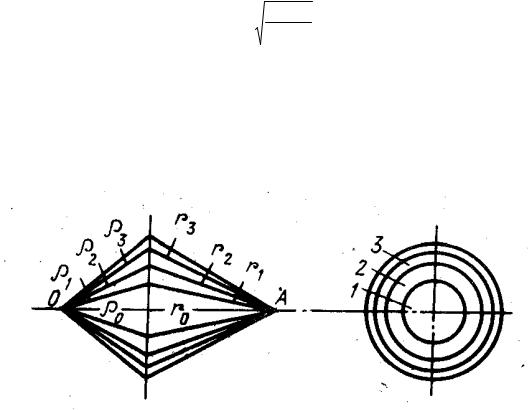
вофазе. В данном случае первая зона Френеля представляет собой круг, а следующие зоны – концентрические кольца (см. рис. 3.2). Радиус внешней границы зоны Френеля с номером n определяется выражением
R |
n |
= nλρ0r0 . |
(3.19) |
|
|
ρ0 |
+ r0 |
|
|
|
|
|
||
Площади всех зон одинаковы и равны
a |
= |
πλρ0r0 . |
(3.20) |
0 |
|
ρ0 + r0 |
|
Основной вклад в поле в точке наблюдения вносят вторичные источники, рас-
Рис. 3.2
положенные в пределах нескольких первых зон Френеля.
Если перемещать плоскость S0 параллельно самой себе вдоль прямой,
соединяющей источник и точку наблюдения, то границы зон Френеля опишут в пространстве эллипсоиды вращения с фокусами в точках, где расположен источник и точка наблюдения. Область пространства между двумя соседними эллипсоидами называют пространственной зоной Френеля.
Таким образом, из проведенного анализа можно сделать вывод о наличии области пространства, существенной для распространения радиоволн. Эта область представляет собой несколько первых пространственных зон Френеля.
3.1.4. Дифракция на крае полубесконечного экрана
Представим себе экран в виде полубесконечного тонкого металлического листа, расположенного на пути распространения радиоволн. Очевидно, что влияние экрана будет значительным, если он пересекает область, существенную для распространения радиоволн. Определим поле в точке наблюдения при наличии экрана. Для этого можно воспользоваться формулой (3.16). Однако значение векторного потенциала на плоскости S0 , которую считаем совмещенной
с плоскостью экрана, неизвестно. Воспользуемся приближением Кирхгофа. В этом приближении считается, что поле в части плоскости, дополняющей плоскость экрана, совпадает с невозмущенным полем, которое имело бы место при
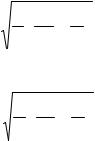
отсутствии экрана; токи на теневой стороне экрана настолько малы, что ими можно пренебречь. Введем декартову систему координат x, y, z , с осью x , на-
правленной вдоль прямой, соединяющей источник и точку наблюдения. При этих допущениях можно преобразовать интеграл (17), воспользовавшись разложением
|
y |
2 |
+ z |
2 |
1 |
|
1 |
|
|
|
ρ + r ≈ ρ0 + r0 + |
|
|
|
+ |
|
(3.21) |
||||
|
|
|
|
|
|
|||||
|
|
2 |
|
|
ρ0 |
|
. |
|||
|
|
|
|
|
|
r0 |
|
|||
Функция, стоящая под знаком интеграла в (3.17) представляет собой произведение медленно меняющихся множителей на быстро осциллирующую функцию. Медленно меняющиеся множители можно считать постоянными и равными их значению в центре первой зоны Френеля. Вынося их за знак интеграла, получаем
|
|
|
|
|
2 |
2 |
) |
|
1 1 |
|
|
|||
A = iI l |
e |
ik (ρ +r ) |
|
(y |
+z |
|
|
|
||||||
0 0 |
∫∫e |
|
2 |
|
|
|
ρ0 |
+ |
r0 |
dydz . |
(3.22) |
|||
|
|
|
ik |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ0r0 |
|
|
|
|
|
|
|
|
|
|
|
|
4πλ |
|
|
|
|
|
|
|
|
|
|
|
|
|
При этом в соответствии с принципом Кирхгофа интеграл берется по части плоскости, дополняющей плоскость экрана. Введем новые переменные интегрирования u и v
|
2 |
|
1 |
|
1 |
|
|
|
u = z |
|
+ |
|
, |
(3.23) |
|||
|
|
ρ0 |
|
|
||||
|
λ |
|
|
r0 |
|
|
||
|
2 |
|
1 |
|
1 |
|
|
|
v = y |
|
+ |
|
, |
(3.24) |
|||
|
|
ρ0 |
|
|
||||
|
λ |
|
|
r0 |
|
|
||
Смысл переменных u и v виден из следующих соотношений. Из формулы (3.19), определяющей радиусы зон Френеля, получаем
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Rn |
|
|
|
|
|
|
|
= n . |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
λ |
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0 |
|
|
r0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Согласно (3.23)-(3.24) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
2 |
+ z |
2 |
1 |
|
|
|
1 |
|
|
|
|
R2 |
|
1 |
|
1 |
|
|
u |
2 |
+ v |
2 |
||||||
|
|
|
|
|
|
+ |
|
|
= |
|
|
|
|
+ |
|
= |
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
λ |
|
|
|
ρ0 |
|
|
|
|
|
|
λ |
|
ρ0 |
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
r0 |
|
|
|
|
|
|
r0 |
|
|
|
|
|||||||||||
Сравнивая (3.25) и (3.26), находим
(3.25)
(3.26)

u2 + v2 |
= nR , |
(3.27) |
|
2 |
|||
|
|
где nR – число зон Френеля, укладывающихся в круге радиуса R , совпадаю-
щем с плоскостью экрана и центром на линии наблюдения. Осуществив замену переменных, получаем
|
i I l |
e |
ik (ρ |
|
+r ) |
|
|
π |
|
2 |
|
π |
2 |
|
|||
A = |
|
0 |
0 |
∫ei |
2 u |
du∫ei |
2 v |
dv . |
(3.28) |
||||||||
|
|
|
ρ0 + r0 |
||||||||||||||
2 4π |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Так как − ∞ ≤ y ≤ ∞ , то и − ∞ ≤ v ≤ ∞. Поэтому второй интеграл в (3.28) |
|
||||||||||||||||
|
|
|
∞ |
π |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
∫ei 2 v2 |
dv = |
|
2i . |
|
|
|
(3.29) |
|||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переменная u в первом интеграле меняется от значения u = u0 , где |
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
||
|
|
|
u0 |
= z0 |
|
|
+ |
1 |
|
|
(3.30) |
||||||
|
|
|
|
λ |
|
ρ |
|
, |
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
r0 |
|
|
|
|||
до бесконечности. Отметим, что в отсутствие экрана u0 = −∞. При этом значе-
ние первого интеграла также определяется (3.29). В этом случае, как и следовало ожидать, получаем выражение для поля диполя в свободном пространстве
I l eik (ρ0 +r0 )
A = 4π ρ0 + r0 .
При наличии экрана из (3.28) получаем
A = |
1 I l |
e |
ik (ρ |
+r ) ∞ |
π |
2 |
||
|
0 |
0 |
∫ei |
2 u |
du . |
|||
|
2i 4π |
ρ0 |
+ r0 |
u |
|
|
||
|
|
|
|
|
|
0 |
|
|
Введем дифракционный множитель
F (u )= |
1 |
∞ i |
π u2 |
du = |
1 |
|
∞ |
cos |
π u2du + |
∞ |
sin |
|
|
|
∫ |
e 2 |
|
∫ |
∫ |
π u2du . |
|||||||||
0 |
2 |
|
|
|
2 |
|
|
2 |
|
2 |
|
|||
|
|
u0 |
|
|
|
|
u0 |
|
|
u0 |
|
|
|
|
(3.31)
(3.32)
(3.33)
Входящие в правую часть выражения (3.33) интегралы могут быть выражены через интегралы Френеля
u |
π u2du , |
|
C(u0 )= ∫0 cos |
(3.34) |
|
0 |
2 |
|
u |
π u2du . |
|
S(u0 )= ∫0 sin |
(3.35) |
|
0 |
2 |
. |
|
|
В результате для дифракционного множителя получаем выражение
F (u |
)= |
1 |
|
1 |
−C(u |
|
|
1 |
− S(u |
|
(3.36) |
2 |
|
2 |
) |
+ i |
2 |
) . |
|||||
0 |
|
|
0 |
|
|
0 |
|
|
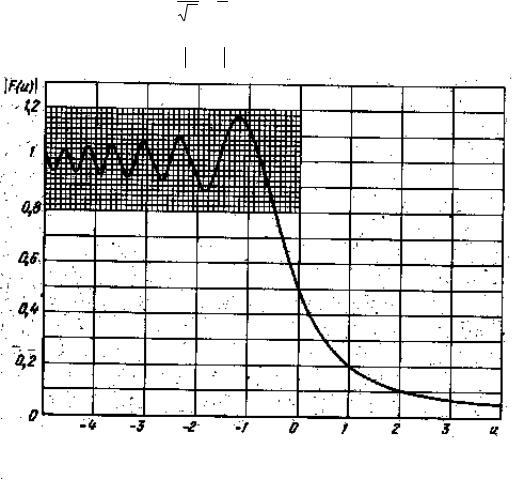
График зависимости F (u0 ) приведен на рис. 3.3.
про-
-
ее
в
Рис. 3.3

Решение задачи о дифракции радиоволн на крае непрозрачного экрана служит основой для анализа условий распространения радиоволн на трассах со сложным рельефом.
3.1.5. Отражение радиоволн от границы раздела двух сред
При исследовании характера распространения радиоволн на различных трассах (вдоль земной поверхности, в условиях городской застройки, внутри зданий и помещений) одним из основных эффектов является отражение радиоволн от различных поверхностей. Характер отражения волны определяется электрическими и магнитными свойствами среды, геометрическими свойствами
поверхности, а также параметрами падающей волны. |
|
|
|
|
|
|
|
|||||
Рассмотрим падение пло- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ской электромагнитной волны на |
|
|
|
|
|
x |
|
|
|
|
||
плоскую границу раздела двух |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сред, характеризуемых ком- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϑ2 |
|
|
||
плексными |
диэлектрическими |
|
|
|
|
|
|
|
|
|
|
|
|
ϑ1 |
|
|
|
|
|
|
|||||
проницаемостями ε1 и ε2 и маг- |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
нитными проницаемостями µ1 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ϑ1 |
|
|
|
|
|
|
|
z |
|||
|
|
0 |
|
|
|
|
||||||
µ2 . При анализе отражения ра- |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
диоволн от границы раздела двух |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сред удобно отдельно рассмот- |
|
|
|
|
|
|
|
|
|
|
|
|
реть два случая – отражение ТЕ- |
|
|
|
|
|
|
|
|
|
|
|
|
иТМ-волн.
Впервом случае вектор
напряженности электрического поля падающей волны перпендикулярен плоскости падения
(см. рис. 3.4), а вектор напряженности магнитного поля – лежит в этой плоскости. Введем декартову систему координат с осью z , направленной перпендикулярно границе раздела. Электромагнитное поле в области z < 0 представим в виде суперпозиции падающей и отраженной волн
Ey(1) = eik1 sinϑ1x (eik1 cosϑ1z + R e−ik1 cosϑ1z ), |
(3.37) |
H x(1) = −eik1 sinϑ1x cosϑ1 (eik1 cosϑ1z − R e−ik1 cosϑ1z ). |
(3.38) |
ζ1 |
|
Здесь ϑ1 – угол падения волны на границу раздела двух сред, k1 = ω |
ε1ε0 µ1µ0 – |
волновое число, R – коэффициент отражения ТЕ-волны. |
|
В области z > 0 поле представляет собой прошедшую волну |
|
Ey(2) = eik2 sinϑ2x T eik 2 cosϑ2z , |
(3.39) |
H x(2) = −eik 2 sinϑ2x cosϑ2 T eik2 cosϑ2z . |
(3.40) |
ζ2 |
|
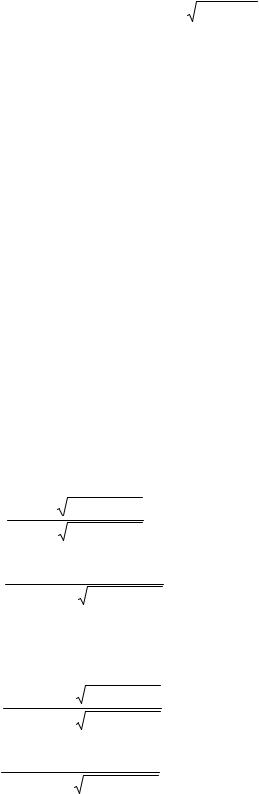
В формулах (3.39)-(3.40) – ϑ2 – угол преломления, k2 = ω ε2ε0 µ2 µ0 – волновое
число, T – коэффициент прохождения ТЕ-волны.
Используя условия непрерывности тангенциальных компонент поля на границе раздела сред (при z = 0 ), легко получить выражения для коэффициента
отражения R и коэффициента прохождения T |
|
|
|
|
||||||||
R = ζ |
2 cosϑ1 −ζ1 cosϑ2 |
, |
(3.41) |
|||||||||
|
|
|
ζ |
2 |
cosϑ +ζ |
1 |
cosϑ |
2 |
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|||
T |
|
= |
|
|
2ζ2 cosϑ1 |
|
|
. |
(3.42) |
|||
|
ζ |
2 |
cosϑ +ζ |
1 |
cosϑ |
2 |
||||||
|
|
|
|
1 |
|
|
|
|||||
Угол преломления ϑ2 связан с углом падения ϑ1 законом Снеллиуса |
|
|||||||||||
k1 sinϑ1 |
= k2 sinϑ2 . |
|
|
|
|
(3.43) |
||||||
В условиях распространения радиоволн вдоль земной поверхности, внутри зданий и помещений часто µ1 = µ2 =1 . Тогда удобно ввести относительный комплексный показатель преломления второй среды относительно первой
n′2 = εε |
2 . |
|
|
|
|
|
(3.44) |
|
1 |
|
|
|
|
|
|
При этом вместо (3.41)-(3.42) получаем |
|
|
|
|
|
|
|
R = cosϑ − |
n |
′2 |
− sin |
2 |
ϑ |
, |
(3.45) |
cosϑ + |
n′2 |
− sin2 |
ϑ |
|
|
||
T = |
2 cosϑ |
|
|
, |
(3.46) |
||
n′2 cosϑ + |
|
n′2 − sin2 ϑ |
|
||||
где ϑ – угол падения волны.
Аналогично для ТМ-волны получаются следующие выражения для ко-
эффициентов отражения и прохождения |
|
|
|
|
|
|
R|| = n′2 |
cosϑ − |
n′2 |
− sin2 ϑ |
, |
(3.47) |
|
n′2 |
cosϑ + |
n′2 |
− sin2 ϑ |
|
|
|
T|| = |
2n |
′ |
cosϑ |
|
. |
(3.48) |
|
− sin2 ϑ |
|||||
n′2 cosϑ + |
|
n′2 |
|
|
||
Из приведенных формул видно, что коэффициенты отражения и прохождения зависят от угла падения волны на границу раздела, а также от частоты волны и параметров среды. Характерные значения относительной диэлектрической проницаемости и удельной электрической проводимости для некоторых видов почвы приведены в табл.3.1
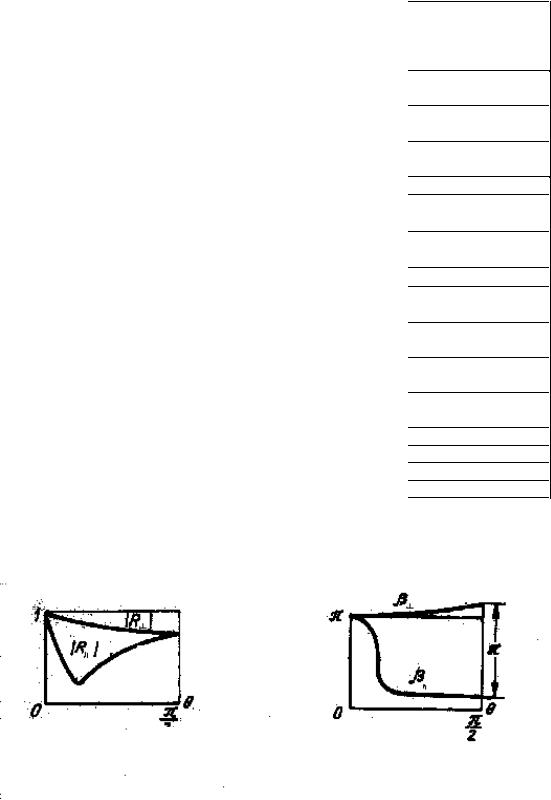
|
|
|
Табл. 3.1 |
Вид земной по- |
Длина волны, м |
ε |
σ , Сим/м |
верхности или по- |
|
|
|
крова |
|
|
1–6 |
Морская вода |
>1,0 |
75 |
|
|
0,1 |
70 |
1–6 |
|
0,03 |
65 |
10–20 |
|
0,003 |
10 |
10–20 |
Пресная вода |
>1,0 |
80 |
10-2–3 10-2 |
|
0,1 |
75 |
1–2 |
|
0,03 |
65 |
10–20 |
|
0,003 |
10 |
2 10-2–3 10-1 |
Влажная почва |
>1,0 |
20–30 |
|
|
0,1 |
20–30 |
5 10-1–1 |
|
0,03 |
10–20 |
1–3 |
Сухая почва |
>1,0 |
3–6 |
10-5–2 10-3 |
|
0,1 |
3–6 |
10-2–7 10-2 |
|
0,03 |
3–6 |
10-1–2 10-1 |
Мерзлая почва |
>1,0 |
3–6 |
10-3–10-2 |
|
0,1 |
|
|
|
0,03 |
|
10-2–10-1 |
Лед (t = - 100C) |
>1,0 |
4–5 |
|
|
0,1 |
3–5 |
10-4–10-3 |
|
0,03 |
2–3 |
10-4–10-3 |
Снег (t = - 100C) |
>1,0 |
1,2 |
10-6 |
|
0,1 |
1,2 |
10-5 |
|
0,03 |
1,2 |
10-5 |
Лес |
>10 |
1,004 |
10-6–10-5 |
|
0,1 |
1,04–1,4 |
10-6–10-5 |
На рис. 3.5. в качестве примера приведены зависимости модулей коэффициентов отражения и аргументов от угла падения для различных поляризаций.
Рис. 3.5

3.2. Модель распространения радиоволн в свободном пространстве
Модель свободного пространства находит широкое применение при анализе условий распространения радиоволн в различных системах связи. Эта модель предполагает отсутствие отражения радиоволн от каких-либо поверхностей. Среда распространения в пределах радиотрассы считается однородной. Не учитывается дифракция волн на препятствиях, рассеяние, рефракция и другие явления, сопровождающие процесс распространения радиоволн.
3.2.1. Излучение элементарного электрического диполя в свободном пространстве
Рассмотрим излучение электрического диполя длиной l , ориентированного вдоль оси z декартовой системы координат. Предположим, что распределение тока вдоль диполя определяется функцией I (z′). Пусть
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
′ |
′ |
|
|
|
|
|
(3.49) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∫I (z )dz = I 0l . |
|
|
|||||||||||
|
|
− |
l |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
Величину |
I 0l |
называют токовым |
моментом. Электромагнитное |
поле на |
|||||||||||
расстоянии r от диполя в дальней зоне (k0r >>1) можно представить в виде [9- |
|||||||||||||||
13] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = − |
ik 0 I 0l |
ζ |
0 |
sinθ eik0r |
, |
(3.50) |
|||||||
|
|
4π |
|||||||||||||
|
|
|
|
|
θ |
|
|
r |
|
|
|||||
|
|
|
|
|
|
Hϕ |
= − |
ik 0 I 0l |
|
sinθ eik0r |
, |
(3.51) |
|||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
4π |
|
|
r |
|
|
|
где k0 =ω |
ε0µ0 |
– волновое число, ζ0 |
= |
µ0 / ε0 |
|
|
– характеристический импеданс |
||||||||
вакуума. В формулах (3.50)-(3.51) используется сферическая система координат r ,θ,ϕ . Средняя плотность потока энергии, определяемая вектором Пойнтинга
|
|
|
SG = 1 Re[EG, HG* |
], |
(3.52) |
|
|
|
2 |
|
|
|
|
имеет радиальное направление и может быть вычислена по формуле |
|
|||||
S |
= |
|
15π(I 0l )2 |
sin2 θ . |
|
(3.53) |
λ2r 2 |
|
|||||
R |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Полная мощность, излучаемая диполем, может быть определена интегрированием потока вектора Пойнтинга через замкнутую поверхность (например, сферу), охватывающую диполь

2π π |
|
|
|
|
|
l |
|
|
2 |
|
PΣ = ∫∫SRr |
2 |
|
2 |
2 |
|
|
|
|||
|
sinθdθdϕ = 40π |
|
I 0 |
|
|
|
. |
(3.54) |
||
|
|
λ |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|
0 |
|
|
|
Используя выражения (3.50) и (3.54), можно выразить напряженность электрического поля в дальней зоне через излучаемую мощность
Eθ = −i 90PΣ sinθ eik0r . |
(3.55) |
|||
|
|
r |
|
|
Если в качестве источника электромагнитного излучения взять |
||||
гипотетический «изотропный излучатель», то излучаемая |
им мощность PΣ |
|||
может быть представлена в виде |
|
|
|
|
PΣ = |
E2 |
4πr 2 , |
(3.56) |
|
0 |
||||
240π |
||||
|
|
|
||
откуда амплитудное значение напряженности электрического поля на расстоянии r от источника принимает следующий вид:
E0 = |
60PΣ . |
|
(3.57) |
|
r |
|
|
Если ввести понятие мощности излучения в заданном направлении |
P(θ,ϕ), |
||
определяемое выражением |
|
|
|
P(θ,ϕ)= S r 2 |
, |
(3.58) |
|
|
R |
|
|
то полная излучаемая мощность получается интегрированием P(θ,ϕ) по телесному углу
2ππ
PΣ = ∫∫P(θ,ϕ)sinθdθdϕ .
0 0
Важной характеристикой любого излучателя является направленного действия D , определяемый следующим образом:
D = 4π P(θ,ϕ)max ,
PΣ
(3.59)
коэффициент
(3.60)
где P(θ,ϕ)max – мощность, излучаемая в направлении главного максимума
диаграммы направленности. С учетом (3.60) из (3.57) получаем выражение для максимального значения амплитуды напряженности электрического поля
E0 = |
60PΣ D . |
(3.61) |
|
r |
|
В некоторых случаях определяют не напряженность электрического поля, а мощность на входе приемника, которая равна произведению плотности потока мощности на эффективную площадь приемной антенны Aef
Pr = SR Aef . |
(3.624) |
|||
Эффективная площадь приемной |
антенны Aef |
связана с коэффициентом |
||
направленного действия D соотношением |
|
|||
A |
= |
D λ2 |
. |
(3.63) |
|
||||
ef |
|
4π |
|
|
|
|
|
||
Если передающая и приемная антенны характеризуются коэффициентами направленного действия D1 и D2 , то мощность на входе приемника
P |
= |
D1D2 λ2 |
P . |
(3. 64) |
|
(4πr )2 |
|||||
r |
|
Σ |
|
Формула (3.64) находит применение при расчете линий радиосвязи, а также в радиолокации.
3.2.2. Потери в свободном пространстве. Максимальная зона обслуживания
Большинство моделей, используемых для расчета радиотрасс в системах мобильной радиосвязи, основаны на простейшей формуле, определяющей мощность принимаемого сигнала PR в свободном пространстве
|
|
|
|
λ |
2 |
|
|
P |
= G |
G |
|
|
|
P , |
(3.65) |
|
|||||||
R |
T |
|
R |
4πd |
T |
|
|
где PT – мощность |
передатчика, |
GT и GR |
– |
коэффициенты усиления |
||
передающей и приемной антенн, d |
– расстояние между приемником и |
|||||
передатчиком, λ – |
длина волны. |
Обычно |
для |
характеристики трассы |
||
распространения вводят величину потерьLP , определяемую выражением |
||||||
|
|
LP = |
PT |
. |
|
(3.66) |
|
|
|
|
|||
|
|
|
PR |
|
|
|
Из формулы (3.65) для распространения в свободном пространстве |
получаем |
LP (дБ)= 20 lg f (МГц)+ 20 lg d(км)−10 lg GT +10 lg GR + 32,45 ; |
(3.67) |
где f – несущая частота сигнала.
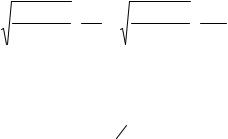
Для изотропных передающей и приемной антенн с коэффициентами усиления, равными 1 (т.е. для идеальных всенаправленных антенн), для трассы прямой видимости потери рассчитываются по формуле
LP [дБ]= 20 lg f [МГц]+ 20 lg d[м]+ 32,45 . |
(3.68) |
Из приведенных соотношений следует, что на трассах прямой видимости принимаемая мощность уменьшается на 6 дБ при каждом удвоении расстояния и при каждом удвоении частоты.
Большинство систем мобильной связи работают в условиях распространения радиоволн при отсутствии прямой видимости. На основе экспериментальных данных были предложены модели для оценки потерь L(d)
при распространении в отсутствие прямой видимости. Эти модели описываются следующими выражениями:
L(d)≈ LP (d / d0 )n , |
(3.69) |
где LP – потери при распространении на трассе прямой видимости длиной d0 ,
d – расстояние между передатчиком и приемником. Показатель степени n для различных условий может изменяться в пределах 3,5 ≤ n ≤ 5 . Для связи внутри зданий, как показывают экспериментальные данные, 2 ≤ n ≤ 4 .
Приведенные соотношения позволяют оценить дальность связи или максимальную зону обслуживания dmax . Для трасс прямой видимости, полагая в
(3.49) PR = PR min , где PR min – минимальная мощность принимаемого сигнала,
обеспечивающая приемлемое значение вероятности ошибки на бит (BER), получаем
dmax = |
PTGTGR |
λ |
= |
PTGTGR |
c . |
(3.70) |
|
PR min |
4π |
|
PR min |
4πf |
|
Для комбинированной радиотрассы, включающей участки прямой и непрямой видимости, можно получить следующее выражение для дальности связи [3,4]:
|
PTGTGR |
|
λ |
|
2 |
1n |
|
d = |
|
|
|
d0 . |
(3.71) |
||
P |
|
|
|||||
4πd |
|
|
|||||
|
R min |
|
|
0 |
|
|
|
|
|
|
|
||||

3.3.Распространение радиоволн над земной поверхностью.
3.3.1.Задача Зоммерфельда
Рассмотрим задачу об излучении элементарного электрического вертикального диполя, расположенного вблизи плоской границы раздела двух однородных сред с диэлектрическими проницаемостями ε1 и ε2. Плотность тока вертикального элементарного диполя зададим в виде
j |
= I lδ(z − zs )δ(x)δ(y)eGz , |
|
(3.72) |
|
z |
|
где I– сила тока в антенне, |
l– раз- |
|
|
меры диполя, δ – символ функции |
|||
|
|
|||
zs |
|
Дирака, ez – |
единичный |
вектор, |
x |
направленный |
вдоль оси |
Z (см. |
|
|
рис. 3.7). |
|
|
|
|
|
|
|
|
|
|
В силу |
симметрии |
задачи |
|
|
электромагнитные поля |
полно- |
|
|
|
стью определяются одной компо- |
||
нентой векторного потенциала Az . Следовательно, уравнение Гельм-
|
гольца может быть записано в |
Рис. 3.7 |
следующем виде: |
|
− в верхнем полупространстве (в атмосфере)
∆A |
+ k2 A |
= −Il δ(z − z )δ(x )δ(y), |
(3.73) |
||
1z |
1 1z |
|
|
s |
|
− в нижнем полупространстве |
|
|
|
|
|
|
∆A |
+ k2 A |
= 0 , |
(3.74) |
|
|
2z |
2 |
2z |
|
|
где k1 = k0 ε1µ1 и k2 |
= k0 ε2 µ2 |
– |
волновые числа в верхнем и нижнем полупро- |
||
странствах. Тангенциальные компоненты напряженности электрического и магнитного поля выражаются через Az следующим образом:
|
1 |
|
∂2 A |
|
|
∂A |
|
|||
Ex = − |
|
|
z |
; |
H x = |
|
z |
; |
|
(3.75) |
i ωεε0 |
|
|
||||||||
|
|
∂x∂z |
|
|
∂y |
|
||||
|
1 |
|
∂2 A |
|
|
|
∂A |
|
||
Ey = − |
|
|
z |
; |
H y = − |
|
z |
. |
(3.76) |
|
i ωεε0 |
|
|
||||||||
|
|
∂y∂z |
|
|
|
∂x |
|
|||
Из условий непрерывности тангенциальных компонент полей на границе раздела при z = 0 получаем граничные условия для вертикальной компоненты векторного потенциала

|
A |
= A |
|
; |
|
|
1 |
|
|
∂A1z |
= |
1 |
|
∂A2z |
при z=0. |
(3.77) |
|
|
|
|
|
|
|
|
|||||||||
|
1z |
2z |
|
|
|
ε1 |
|
|
∂z |
ε2 |
|
∂z |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
Фурье |
Будем искать решение для векторного потенциала с помощью преобразования |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Az (x, y) |
|
∞ |
∞ |
~ |
(kx ,ky , z)exp(ikx x + iky y)dkx dky , |
(3.78) |
|||||||||
|
= ∫ |
∫ |
Az |
|||||||||||||
|
|
|
|
−∞ −∞ |
|
|
|
|
|
|
|
|
|
|
||
~ |
(kx ,ky , z)– фурье-образ искомой функции. Используя интегральное представление |
|||||||||||||||
где Az |
||||||||||||||||
для δ-функции |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
||
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|||
|
|
δ(x) |
= |
|
1 |
|
|
∞ exp(ikx x)dkx , |
(3.79) |
|||||||
|
|
|
|
|
|
|||||||||||
−∞
получаем обыкновенные дифференциальные уравнения для спектральных компонент векторного потенциала
d |
2 |
~ |
|
|
2 ~ |
I l |
|
|
|
A1z |
2 |
|
|||||
|
|
+ (k1 |
−k )A1z = − |
|
δ(z − zs ); |
|||
dz2 |
4π2 |
|||||||
d |
2 |
~ |
|
|
2 ~ |
|
|
|
A2z |
2 |
|
|
|||||
|
|
|
|
|
+ (k2 |
−k )A2z = 0 , |
|
|
dz |
2 |
|
|
|||||
|
|
|
|
|
|
|||
где k 2 = kx2 +ky2 .
Граничные условия для уравнений (3.80)-(3.81) принимают вид
~ |
~ |
~ |
|
1 |
|
~ |
|
|||
1 ∂A1z |
|
|
∂A2z |
|
||||||
A1z = A2z , |
|
|
|
= |
|
|
|
. |
||
ε1 ∂z |
ε2 |
∂z |
||||||||
|
|
|
|
|||||||
Решение этих уравнений можно представить в виде
~ |
|
i |
κ z |
|
|
|
|
|
−i κ |
z |
|
i I l |
i κ |
|
|
z−z |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||
A |
= C e |
1 |
|
+C |
2 |
e |
|
2 |
|
|
+ |
|
e |
1 |
|
s |
|
, |
|||
|
|
|
|
|
|
|
|||||||||||||||
1z |
1 |
|
|
|
|
|
|
|
|
|
|
|
8π2 κ1 |
|
|
|
|
|
|
||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= C |
i κ |
z |
+C |
|
|
e |
−i κ |
|
z |
, |
|
|
|
|
|
|
|
||||
A |
e |
2 |
|
4 |
2 |
|
|
|
|
|
|
|
|
||||||||
2z |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(3.80)
(3.81)
(3.82)
(3.83)
(3.84)
где κ |
1 |
= |
k 2 |
−k 2 , κ |
2 |
= |
k 2 −k 2 , |
C −C |
4 |
– произвольные постоянные. Последнее |
|
|
|
1 |
|
|
2 |
|
1 |
|
|||
|
|
|
|
|
|
|
~ |
описывает плоские волны, распространяющиеся от ис- |
|||
слагаемое в выражении для A1z |
|||||||||||
точника, расположенного в точке z = zs . C1 |
– амплитуда плоской волны, распростра- |
||||||||||
няющейся в положительном направлении оси z , C2 – в отрицательном. Следовательно, C1 характеризует амплитуду волн, отражающихся от плоскости z = 0 . Постоянную C2 следует положить равной нулю, так как нет источников, расположенных на бесконечности. Аналогично, C3 = 0 . Константы C1 и C4 находятся из граничных условий

|
|
|
|
|
|
|
|
C + |
|
i I l |
|
|
|
ei κ1zs = C |
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
8π2 κ1 |
|
|
4 |
(3.85) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i κ1 |
|
|
|
|
i I l |
|
|
i κ z |
|
|
|
|
|
i κ2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 s |
|
|
|
|
|
|
C4 , |
|
|
|
ε1 |
|
|
|
− 8π2 κ1 |
|
|
|
= − ε2 |
|
||||||||||||
|
|
|
C1 |
e |
|
|
(3.86) |
|||||||||||||||
откуда |
|
|
|
|
ε2 κ1 − ε1κ2 |
|
|
|
i I l |
|
|
|
|
|
|
|
|
|
||||
C |
|
= |
|
|
|
|
|
|
|
ei κ1zs , |
|
|
(3.87) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
ε2 κ1 + ε1κ2 8π2 κ |
1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2ε2 κ1 |
|
|
|
i I l |
|
|
|
i κ z |
|
|
|
||||
C |
4 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
e |
1 s . |
|
|
(3.88) |
||
|
ε2 |
κ1 + ε1κ2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
8π2 κ1 |
|
|
|
|
|||||||||||||
Таким образом, решение задачи Зоммерфельда в интегральной форме можно записать в следующем виде:
в верхнем полупространстве
A1z (x, y)= |
|
i I l |
|
∞ ∞ |
ei κ1 |
|
z−zs |
|
+ ε2 κ1 − ε1κ2 |
ei κ1(z+zs) exp(ikx x + iky y) |
dkx dky |
; |
|||||||||||||
|
|
|
|
||||||||||||||||||||||
|
8π2 −∞∫ −∞∫ |
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ε2 κ1 + ε1κ2 |
|
|
|
|
|
|
|
|
|
|
κ1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.89) |
||
в нижнем полупространстве |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
A |
(x, y) |
= |
i I lε |
2 |
∞ ∞ ei κ1zs e−i κ2z |
|
exp ik |
|
x + ik |
|
y dk |
dk |
|
. (3.90) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
4π2 |
−∞∫ −∞∫ ε2 κ1 + ε1κ2 |
|
|
|
||||||||||||||||||||
|
|
2z |
|
|
|
( |
x |
|
y |
) |
x |
|
y |
|
|
|
|||||||||
В полученных выражениях можно от двойных перейти к однократным интегралам. Для этого воспользуемся полярными координатами как в плоскости (x, y), так и в
плоскости (kx ,ky )
x = ρ cosϕ, |
kx = k cosφ, |
(3.91) |
|
y = ρsinϕ, |
ky = k sinφ. |
||
|
где ρ = x 2 + y 2 . Заметим, что интегралы по переменной φ выражаются через функции Бесселя первого рода нулевого порядка J0 (x)
|
|
1 2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
exp(ik ρ cos(φ −ϕ))dφ =J0 (k ρ). |
|
|
|
|
|
(3.92) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2π ∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Используя это соотношение, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
iIl |
∞ i κ |
1 |
|
z−z |
|
|
|
ε |
κ |
1 |
−ε κ |
i κ |
(z+z ) k |
|
J |
0 |
(k |
|
ρ)dk |
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
A1z = |
|
|
∫ e |
|
s |
|
+ |
2 |
|
|
1 2 |
e |
1 |
s |
|
|
|
|
|
(3.93) |
||||||||||||
4π |
|
|
|
|
ε |
κ |
1 |
+ε κ |
|
|
|
|
|
|
κ |
1 |
|
|||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
iIl ε2 |
∞ |
i κ1zs −i κ2 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
A2 z = |
∫ |
e |
|
|
e |
|
|
k J0 (k ρ)dk . |
|
|
|
|
(3.94) |
|||||||||||||||||
|
|
2π |
ε κ |
1 |
+ε κ |
2 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
