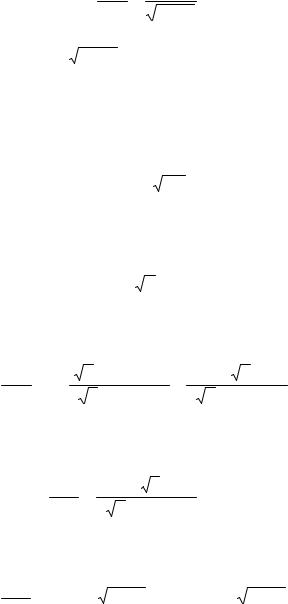
|
|
|
En+1 = |
A1+γn . |
|
|
|
|
|
|
|
(3.229) |
||
|
|
|
E0 |
|
3n +1 |
|
|
|
|
|
|
|
|
|
Здесь множитель 1/ |
3n +1 связан с многократной дифракцией радиоволн на |
|||||||||||||
крышах зданий, а фактор A1+γn |
|
описывает затухание в кронах деревьев. |
||||||||||||
Для практических расчетов из выражений (10)-(11) при малых значениях |
||||||||||||||
α и g можно получить приближенные формулы. Заметим, |
что при малых |
|||||||||||||
значениях аргумента X ≈ πg2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
F (X )≈ [ πX − 2X ei π / 4 ]eiπ / 4+iX . |
|
|
|
(3.230) |
|||||||
Для наиболее часто встречающихся на практике случаев 0 ≤ X < 0,3 . При этом |
||||||||||||||
из (4) следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ds,h / |
|
d ≈ −1/ 2 + g ei π / 4 , |
|
|
|
|
(3.231) |
||||
и из (11) при 0,1 ≤ g < 0,3 и достаточно больших n ( n ≥ 6 )получаем |
||||||||||||||
E |
n+1 |
|
2 − A e−i |
∆k∆d |
+ |
2 2 |
|
|
g ei |
π |
/ 4 |
|
(3.232) |
|
|
≈ A |
|
−i∆k∆d |
|
−i |
∆k∆d |
|
. |
||||||
E0 |
|
2 2 − A e |
2 2 |
− A e |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
Пусть 0,1 ≤ |
|
1/ 2 − 2A exp(− i ∆k∆d) |
|
< g < 0,3 , тогда вместо (3.232) имеем |
|
||||||
|
|
|
|||||||||
|
|
En+1 ≈ |
2 2 |
|
|
gA . |
(3.233) |
||||
|
|
E0 |
2 2 − A e−i ∆k∆d |
|
|
||||||
Аналогично из (12) получаем |
|
|
|
||||||||
En+1 ≈ A(Aγn / |
3n +1 + 2g(1 − Aγn / 3n +1)ei π / 4 ), |
(3.233) |
|||||||||
|
|
E0 |
|
|
|
|
|
|
|
|
|
и далее для n >>1 |
En+1 |
|
|
|
|
|
|
|
|
||
|
|
|
≈ 2Ag . |
|
(3.234) |
||||||
|
|
|
|
|
|||||||
|
|
|
E0 |
|
|
|
|||||
В отсутствие деревьев вместо (20) и (22) соответственно получаем |
|
||||||||||
|
|
|
|
|
En+1 |
≈1,55g . |
(3.235) |
||||
|
|
|
|
|
E0 |
|
|
|
|||
|
|
|
|
|
En+1 |
|
≈ 2g . |
(3.236) |
|||
|
|
|
|
|
E0 |
||||||
|
|
|
|
|
|
|
|
||||
3.5.4.Одновременный учет отражения от земной поверхности и дифракции
Всистемах мобильной связи в городских условиях приемная антенна часто расположена на небольшой высоте над земной поверхностью существенно ниже уровня крыш окружающих зданий, т.е. в отсутствие прямой видимости. В этих условиях сигнал от базовой станции попадает в приемную антенну в результате многократных отражений от стен зданий и других поверхностей, в результате дифракции на кромках и углах зданий, а также в результате рассеяния на различных малых объектах. Таким образом, принимаемый сигнал представляет собой сумму сигналов, пришедших вдоль различных траекторий с различным затуханием и фазовым сдвигом. В результате многолучевого распространения амплитуда принимаемого сигнала может испытывать значительные вариации относительно среднего уровня. Аналогичные условия наблюдаются при распространении радиоволн внутри помещений. В связи с этим возникает задача расчета радиоканала с учетом многократных отражений радиоволн и дифракции на кромках зданий (в городских условиях) или на кромках стен, перегородок (внутри помещений).
Полное поле в точке приема можно представить в виде суммы нескольких лучей: прямого луча; отраженного от земной поверхности луча; дифракционного луча, испытавшего дифракцию на крае препятствия; луча, пришедшего в точку наблюдения после отражения от земной поверхности и в результате дифракции на крае препятствия; луча, последовательно испытавшего дифракцию и отражение от земной поверхности. Соответствующее выражение имеет вид
ET = Elos + Eref + Edifr + Edr + Erd , |
(3.237) |
где Elos и Eref – компоненты поля, соответствующие прямому и отраженному
от земной |
поверхности |
лучам, Edifr |
– компонента поля, соответствующая |
дифракции |
на кромке |
препятствия, |
Edr и Erd характеризуют сигналы, |
отраженные и земной поверхности и испытавшие дифракцию. Выражения для этих компонент можно представить в следующем виде:
Elos = |
E0 |
|
|
e−ikd1 , |
|
|
|
|
|
(3.238) |
||||
|
d1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E |
ref |
|
= |
E0 |
|
R (ψ,ε)e−ikd 2 , |
|
|
|
|
(3.239) |
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
d2 |
|
v |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
E0 |
|
′ |
′ |
−ikd 3 |
|
|
|||
Edif |
= |
|
|
|
|
|
Dv,h (β,φ1 ,φ1 |
, s1 |
, s1 )e |
|
|
, |
(3.240) |
|
|
d3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
E0 |
|
′ |
|
′ |
|
−ikd 4 |
|
|
||
Edr |
= |
|
|
|
|
Dv,h (β,φ2 ,φ2 |
, s2 |
, s2 )e |
|
, |
(3.241) |
|||
|
d4 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
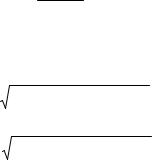
E0 |
′ |
′ |
−ikd 5 |
|
|
Erd |
= |
|
Dv,h (β,φ3 ,φ3 |
, s3 , s3 )e |
|
, |
(3.242) |
d5 |
|
||||||
|
|
|
|
|
|
|
где E0 – напряженность электрического поля на единичном расстоянии от источника, Rv,h и Dv,h коэффициенты отражения и дифракции, приведенные в
[29]. В формуле (3.239) ε – комплексная диэлектрическая проницаемость почвы. Угол отражения ψ определяется выражением
ψ= arctg h0 + h2 .
a0 + a1
Вформулах (3.238)-(3.243) использованы следующие обозначения:
|
|
|
|
|
|
|
|
d1 = (h0 − h2 )2 + (a0 + a1 )2 , |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
d2 = (h0 + h2 )2 + (a0 + a1 )2 , |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
′ |
, |
|
|
|
|
′ |
, |
|
|
|
||
|
|
|
|
d3 = s1 + s1 , |
|
|
|
d4 = s2 + s2 |
d5 = s3 + s3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
− h1 |
|
|
|
|
|
|
|
|
|
|
+ h1 |
|
|
|
|||||||
|
|
|
|
|
|
h0 |
|
|
, |
θhp2 |
|
|
|
|
h0 |
|
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
θhp1 = arctg |
a |
|
|
|
= arctg |
|
a |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||
φ1 |
= φ2′ = |
π +θhp1 , |
|
|
|
φ3′ = |
|
|
π |
+θhp2 , |
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
′ |
|
′ |
= |
(h0 − h1 ) |
, |
|
|
|
|
′ |
|
|
(h0 + h1 ) |
|
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
s1 |
= s2 |
sinθhp1 |
|
|
|
s3 = |
|
|
sinθhp2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|||||
θ |
|
|
= arctg |
|
|
|
|
, |
θ |
|
= arctg |
|
|
|
|
|
, |
||||||||||
|
|
|
− h |
|
|
|
|
+ h |
|
||||||||||||||||||
|
hp3 |
|
|
h |
|
|
|
|
hp4 |
|
|
|
h |
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
||||
φ1 = φ3 = 2π −θhp3 , |
|
|
|
φ2 = 2π −θhp4 , |
|
|
|
|
|
||||||||||||||||||
s |
= s |
= |
(h1 − h2 ) |
, |
|
|
|
s = |
(h1 + h2 ) |
, |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
3 |
|
cosθhp3 |
|
|
|
|
|
2 |
|
|
sinθhp4 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(3.243)
(3.244)
(3.245)
(3.246)
(3.247)
(3.248)
(3.249)
(3.250)
(3.251)
(3.252)
На рис. 3.31 в качестве примера приведена зависимость относительного уровня принимаемого сигнала в зависимости от расстояния до препятствия. Геометрия задачи показана на рис. 3.30. Из приведенной зависимости видно, что на небольших расстояниях от препятствия заметен эффект экранировки, приводящий к уменьшению амплитуды принимаемого сигнала примерно на 30 дБ. На расстоянии около 7 м появляется прямой сигнал и амплитуда суммарного сигнала становится сравнимой с амплитудой сигнала в свободном пространстве.
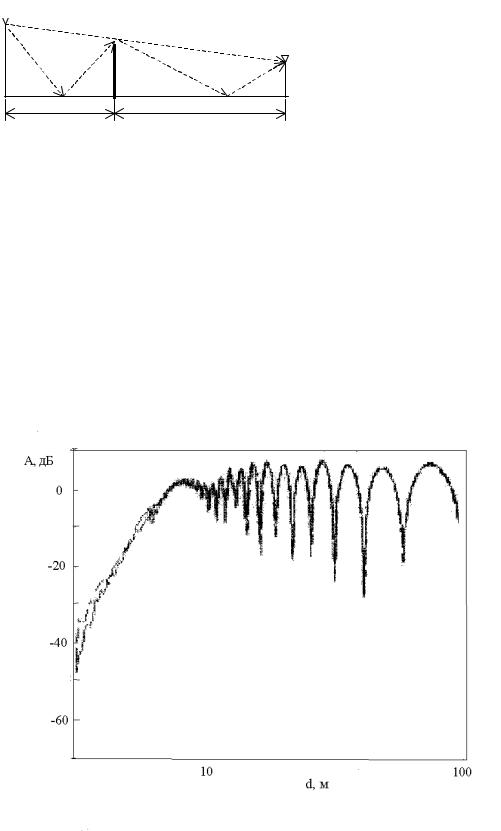
T |
h0=1,5м |
|
h1=1м |
||
|
||
|
R |
|
|
h2=0,5м |
a0 |
a1 |
Рис. 3.30
Рис. 3.31