9.2. Интерполирование кривых с помощью алгебраических полиномов канонического вида

Алгебраической кривой (полиномом степени k) называют выражение

P(х)=C₀+C₁х+C₂х²+…+C_k х^k, (9.6)

где х – независимый параметр, k - степень полинома. Выражение (9.6) называются каноническим видом полиномов. При его использовании затрачивается минимальное число операций в расчёте значений P(х) в случае применения схемы Горнера, когда вычисления производятся по формуле P(х) = C₀ + х(C₁+х(C₂ +…+ х(C_k-1 +C_k х)…)). Также канонический вид полиномов имеет наименьшее число коэффициентов, что минимизирует объем памяти, требуемой для его хранения.

Рассмотрим в общем виде задачу интерполирования (точного построения), в которой требуется точно выполнить набор условий, накладываемых в отдельных узловых точках, при помощи единой алгебраической кривой P(х) наименьшей степени k.

Постановку задачи можно сформулировать следующим образом:

построить полином P(х) наименее возможной степени k, который:

1) проходит через заданные точки P₀ =(х₀, у₀),P₁=(х₁, у₁), … ,P_n = (х_n, у_n);

2) в некоторых точкахP_i =(х_i, у_i),производные полинома P(х) до некоторой степени j должны принимать заданные значения: P(х _i)= у_i ,... , P ^j(х _i)= у_i ^j .

Для отдельных частных случаев решение задачи найдено в явной форме (в виде готовых формул, не требующих предварительного составления и решения уравнений). Так, при простом прохождении функции через узлы без учета ее производных в узлах (пункт 2 общей постановки) решение рассмотренной задачи дают интерполяционные полиномы Лагранжа и Ньютона. При дополнительном задании первых производных в узлах решение дает полином Эрмита. Данные полиномы дают решение в готовом виде. Их общим недостатком является увеличенное число элементарных операций, затрачиваемых при расчете значений по сравнению с полиномом канонического вида. Его можно устранить, применяя группировку слагаемых при степенях параметра х.

Рассмотрим общее решение сформулированной задачи интерполирования для полинома Р(x) канонического вида минимально возможной степени k на некотором наборе узлов x₀, x₁,…, x_n.

При расчете минимального значения k исходят из следующих соображений: число неизвестных коэффициентов С₀, C₁, …,C_k в полиноме равно (k+1). Общее число условий, накладываемых на функцию в узлах, складывается из:

1. количества заданных точек P₀,P₁,…,P_n – их число равно (n+1);

2. общего числа производных 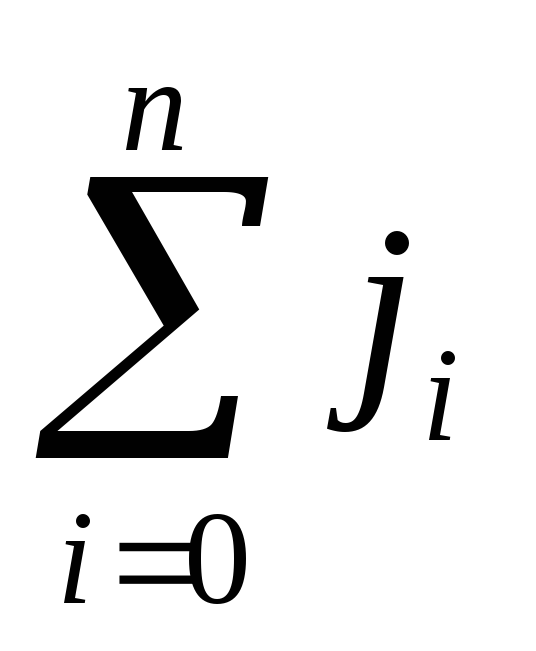, заданных в этих точках.

Решение задачи интерполирования всегда существует и является единственным, если k+1 = n+1+. При выполнении этого условия число неизвестных равно числу уравнений. Отсюда следует предварительная величина минимальной степени интерполирующего полинома:

k=n+. (9.7)

После определения k решается задача об определении коэффициентов полиномаС = {С₀,С₁,…,С_n}. Для этого составляется система из k уравнений, каждое из которых образуется подстановкой значения x = x_i в условие первого типа y(x_i) = y_i, что дает уравнение вида: C₀+C₁x_i+C₂x_i²+…+C_kx_i^k=y_{i .}

Для раскрытия условия на первую производную y(x_i) = y_i выполняем подстановку x = x₁ в производную. Получаем уравнение: C₁+2C₂x_i +…+kC_kx_i^k-1=y_i.

Производные более высоких порядков раскрываются аналогично. Итоговую систему линейных уравнений можно представить в виде:

AC=Y, (9.8)

где C=(C_0,C₁,…,C_k) – искомый вектор коэффициентов полинома,

Y – вектор заданных точечных значений функции и ее производных,

A – матрица коэффициентов.

Искомый вектор неизвестных коэффициентов равен:

C = A^-1Y, (9.9)

где A^-1 –матрица, обратная к А .

Пример 1. Заданы:

1) значения полинома в трех узлах: y(x₀) = y₀; y(x₁)=y₁; y(x₂)=y₂ и

2) значение первой производной в узле x₀ : y(x₀)=y₀.

Необходимо построить интерполирующий полином наименее возможной степени.

Решение.

1.Определение степени полинома k. Число n=2, суммарное число заданных значений производных =1. Следовательно, по формуле (9.7) k=3 и полином имеет вид: P(x) = C₀ + C₁x + C₂x² + C₃x³, где (С₀, C₁, C₂, C₃) - постоянные коэффициенты.

2.Определение коэффициентов полинома. Из условий вида 1) подстановкой вместо х значений х₀, х₁, х₂ получаем уравнения

C₀+C₁x₀+C₂x₀²+C₃x₀³ = y₀;

C₀+C₁x₁+C₂x₁²+C₃x₁³ = y₁;

C₀+C₁x₂+C₂x₂²+C₃x₂³ = y₂ .

Из условия вида 2) подстановкой х = х₀ в P(x) = C₁ + 2C₂x + 3C₃x² получаем уравнение C₁ + 2C₂x₀ + 3C₃x₀² = y₀.

Объединяя полученные уравнения, получаем систему вида (9.8), где

; ; .

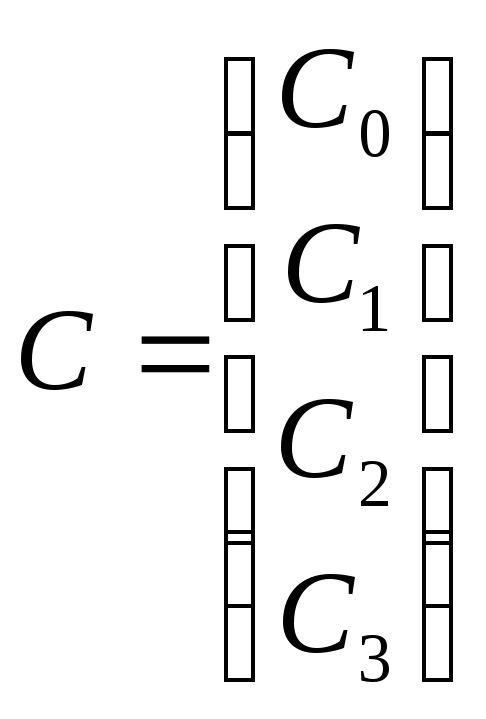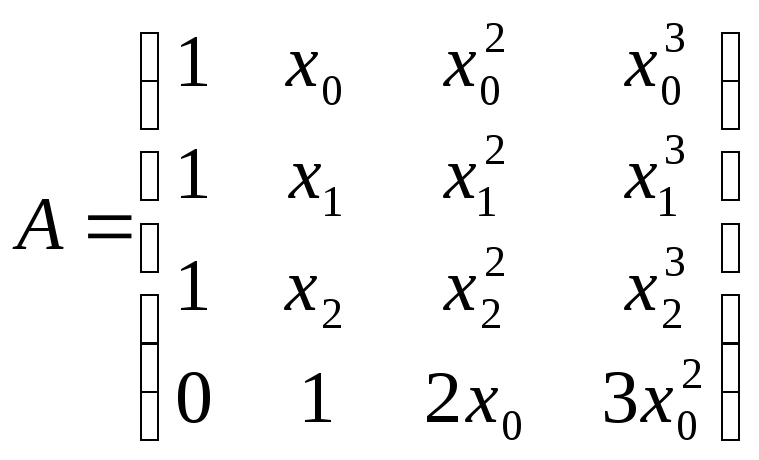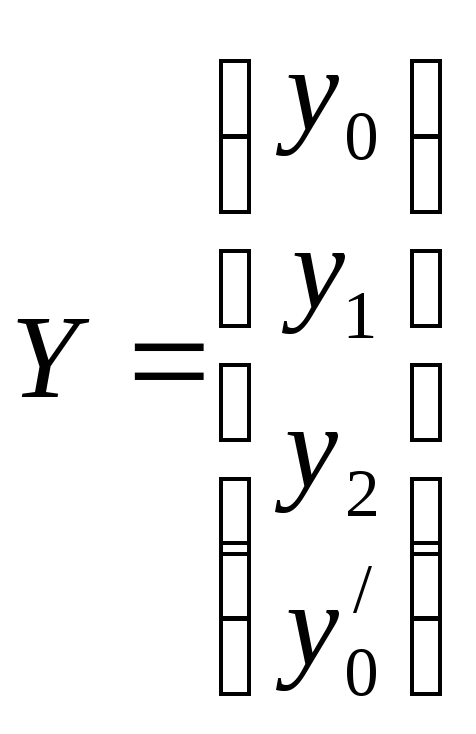Решением системы является вектор C=A^-1 *Y.

Замечание. При специальном задании геометрических условий возможны случаи, когда реальная степень полинома меньше значения, задаваемого формулой (9.7). Например, если в приведенном выше примере задать условия вида:

0. y(1)=0; y(2)=1; y(3)=2; 2) y(1)=1; то при этом

;;

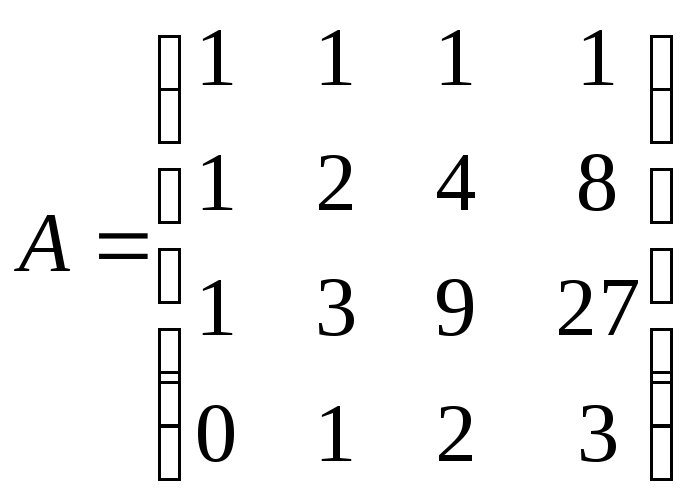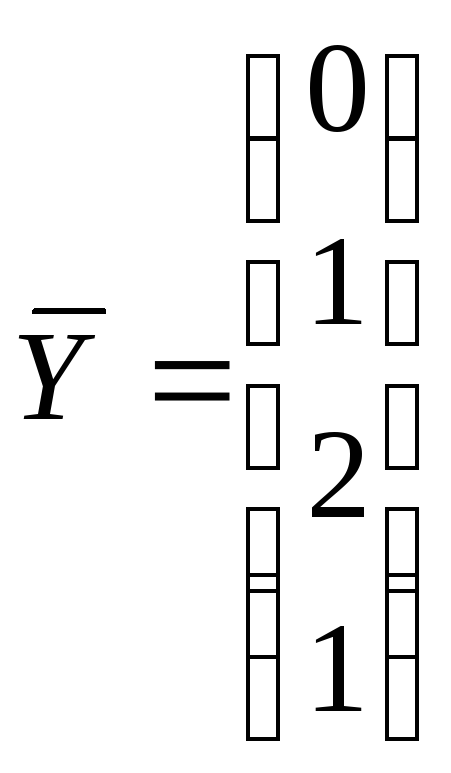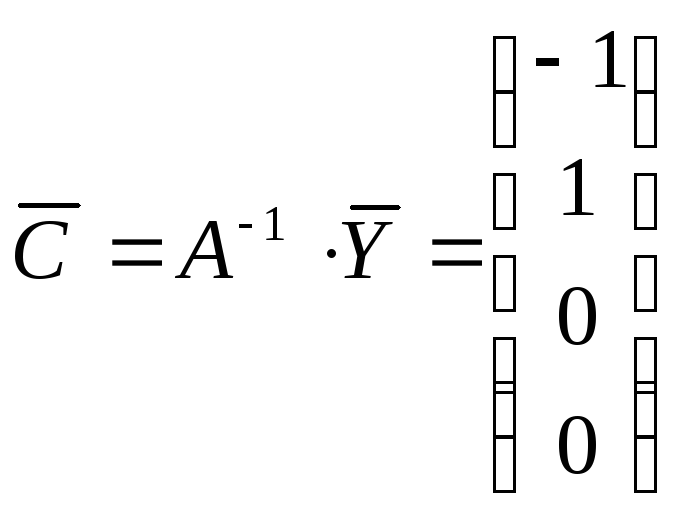; P(x) = x-1; k = 1 < 3.

Таким образом, в данном частном случае реальная степень интерполирующего полинома равна 1. Геометрический смысл примера понятен из Рис.9.1: точки Р₀, Р₁, Р₂ лежат на прямой y=(x-1), угол наклона производной y(x₀) также равен углу наклона этой прямой, поэтому в данном случае вместо кубической параболы (k=3) минимальную степень полинома получаем на наклонной прямой, имеющей k=1.

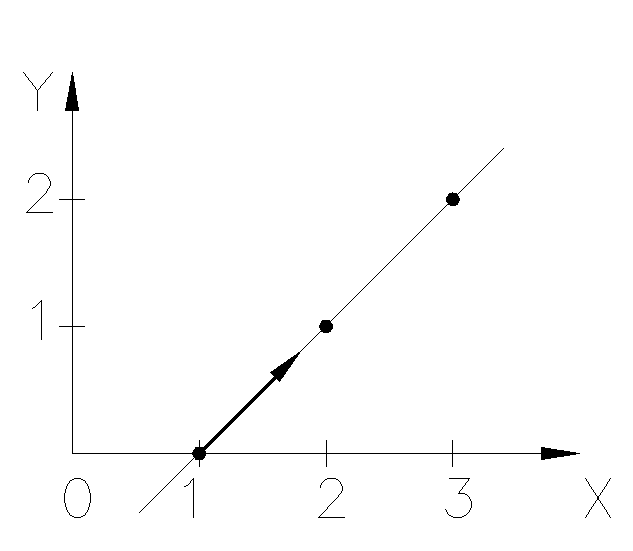
Рис.9.1

Если рассматривать частный случай y(1)=1; y(2)=1; y(3)=1; 2) y(1)=0 ;

то векторыY и С будут следующими:

; .

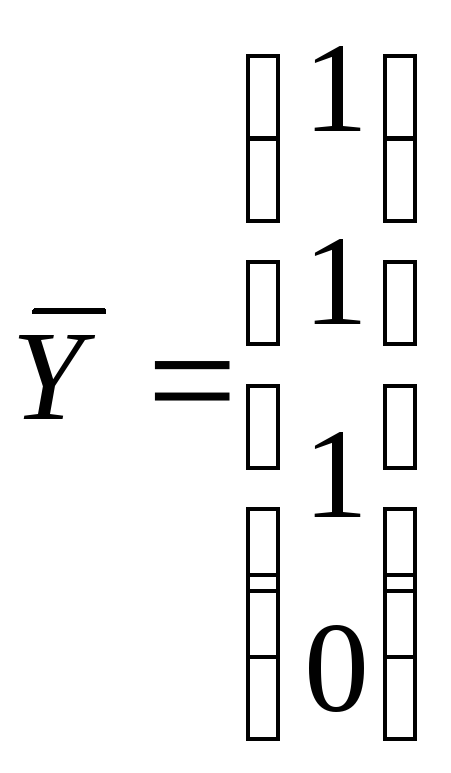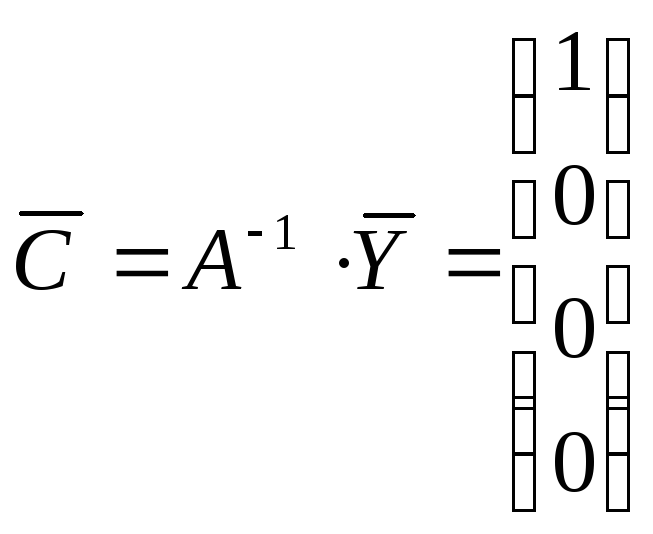Интерполирующий полином примет вид: P(x) = 1. В данном случае реальное значение k=0, т.к. все точки лежат на прямой y=1 и угол наклона производной равен 0 (Рис. 9.2).

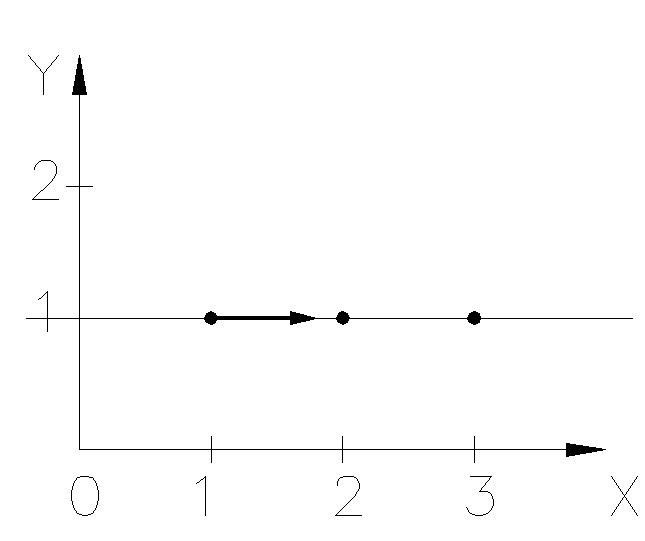
Рис. 9.2

В обоих приведенных примерах имеет место дублирование условий, наложенных на интерполирующих полином, поскольку некоторые из них оказываются излишними, описывающими объект, уже полностью определённый предыдущими условиями. Рассмотренные примеры показывают, что окончательное значение степени полинома k может быть уточнено только после расчета его коэффициентов.

Расчет одного значения полинома канонического вида степени k по схеме Горнера требует выполнения k сложений и k умножений. Сложность вычисления линейная по k - О(k¹).

Вопросы для проверки знаний.

1. Какое выражение называют алгебраической кривой (полиномом) ?

2. В чем заключаются преимущества канонической формы представления полиномов ?

3. Для каких частных случаев задачи интерполирования по заданным узлам существуют явные решения в формульном виде ?

4. По какой формуле может быть рассчитана предварительная величина минимальной степени интерполирующего полинома ?

5. Каким образом составляются линейные уравнения по условиям, заданным в узлам на интерполирующий полином ?

6. Почему после расчета коэффициентов полинома его степень может оказаться меньше ее предварительной минимальной величины ?

Практические задания.

1. Найти степень полинома k и матрицу А (по возможности в численном виде) для определения коэффициентов полиномаС =(C₀, C₁, …,C_k ) для следующих наборов геометрических условий:

а) n=1; х₀ = -1 ; х₁ =1 ;

у(-1) = 1 ; у(-1) = 2; у (-1)=3; у(1) = 1,5;

б) n=3; х₀ = 0 ; х₁ = 1 ; х₂ =2 ; х₃ =3;

у(х₀) = 0 ; у (х₁)= 2 ; у(х₂) =5 ; у (х₃)=6;

в) n=2; х₀ = -1 ; х₁ = 0 ; х₂ =1 ;

у(х₀) = -2 ; у(х₀) = 2; у(х₁)= у(х₁)=1; у(х₂) = 1,5; у(х₂) =0;

г) n=2; х₀ = 1 ; х₁ =3 ; х₂ =4 ;

у(х₀)=у(х₀)=1; у(х₁)=2; у(х₁)=у(х₁)=0; у(х₂)=1; у(х₂)= - 2.