05 семестр / Лекции и семинары / Лекции

31

Определение изменения энтальпии газов в дифференциальной форме

Пусть

Физический смысл :

при

Следовательно

По закону Джоуля известно, что энтальпия идеальных газов зависит от температуры и не зависит от давления:

Для идеальных газов

Так как не зависит от характера процесса, то формула справедлива для любых процессов идеального газа. Для газов при , когда имеем:

при

32

для этого составлены таблицы энтальпии при разностях температур

Для реальных веществ в общих случаях:

На основании дифференциального уравнения получаем:

термическая расширяемость

Выражение первого закона термодинамики во форме для идеального газа

В заключении следует отметить, что две формы математического выражения первого закона термодинамики являются равнозначными

11.Математические характеристики функций

состояния и функций процесса

Все величины, изучаемые в термодинамике можно разложить на функции состояния и функции процесса. Величины характеризуют рабочее тело в заданном

33

состоянии, изменения этих величин зависит от начального и конечного состояния и не зависит от характера процесса:

полные дифференциалы, их интегрирование не зависит от характера процесса.

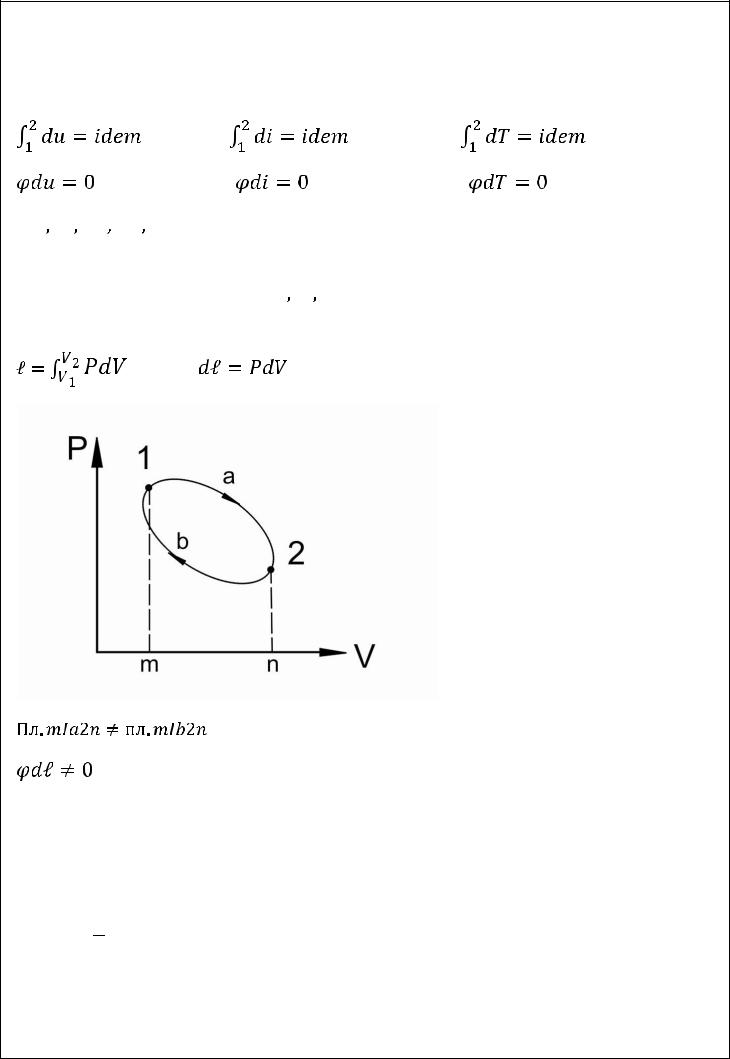
К функциям процесса относятся . Эти величины имеют другие математические характеристики.

не является полным дифференциалом

не является полным дифференциалом

12. Энтропия идеального газа

Энтропия функция состояния

34

Энтропия вводится математическим путем

Проведем операцию приведения этого уравнения к температуре

Это выражение обладает свойством полного дифференциала:

т.к. ,

Обозначим

функция состояния или свойство рабочего тела, называемое энтропией.

Абсолютная величина энтропии в технических расчетах не определяется (однако условно можно принять энтропию газа равной нулю при и

зависит от начального и конечного состояния.

После интегрирования получим

При

36

Изменения энтропии (

Определяются по соотношению:

Основное свойство диаграммы состоит в том, что площадь между линией процесса и осью абсцисс выражает теплоту данного обратимого процесса.

Диаграмма называется тепловой диаграммой. Знак теплоты всегда определяется знаком изменения энтропии в процессе.

теплота подводимая

теплота отводится

По направлению процесс можно судить о знаке теплоты

37

14. Исследование обратимых термодинамических процессов

Все параметры изменяются, что приводит к изменению состояния рабочего тела.

Термодинамические процессы происходят в результате теплового и механического взаимодействия рабочего тела сокрушающей средой. Поэтому кроме изменения параметров состояния в термодинамических процессах могут участвовать теплота ,

работа изменения объема , техническая работа , как со знаком так и с –

Объектом исследования в термодинамических процессах является определение теплоты и работы процесса.

Выделяются 4 вида процессов, характеризующихся постоянством одного из параметров состояния

процессы

Кроме указанных имеет и еще множество других обратных процессов, которые называются политропными. Все они рассматриваются как обратные, идеальные.

14.1. Изохорные процессы.

Изохорные процессы – происходят при постоянном объеме рабочего тела (нагревание и охлаждение газа в закрытом сосуде);

Изображение диаграмме

38

Изображение в диаграмме

Кривая логарифмическая

39

С увеличением температуры уклон увеличивается. Изохоры для различных объемов изображаются эквидистантными кривыми с одинаковыми угловыми коэффициентами при одной и той же температуре.

14.2. Изобарные процессы

Изображение в диаграмме

40

(

При

Рассмотрение сжатие и определяются по общим формулам

и из таблицы Из первого закона термодинамики для закрытой системы

Для атомных газов ( воздух)

при

Это уравнение Майерса

на величину Изображение изобары в диаграмме