05 семестр / Лекции и семинары / Лекции

131

при входе

на выходе

всегда

Коэффициент можно определить, если известен характер процесса. Без учета трения потока в диффузоре можно считать обратимым адиабатическим сжатием.

в диффузорах работа сжатия за счет снижения кинетической энергии

скорость потока при входе в диффузор

скорость на выходе из диффузора

132

22.8. Выбор формы канала диффузора Форма канала диффузора определяется изменением скоростей потока. Форму канала

можно выбирать по кривой удельной площади но рассматривать ее надо в обратном направлении, принятым для сопла.

Согласно кривой диффузорный канал может иметь три варианта формы канала

133

Сужающий канал

Сужено-расширяющийся канал

134

Расширяющийся канал

22.9. Параметры торможения адиабатического потока

Если в поток газа поместить твердое тело, то в некоторой точке встречи потока с телом этот поток полностью затормозиться, т.е. скорость его будет равна нулю. Такая точка называется критической. Это приводит к изменению параметров набегающего потока

T, P, до параметров торможения в критической точке.

Рассмотрим случай, когда в точке торможения нет теплообмена между заторможенным газом и твердым телом. В этом случае торможение является адиабатным.

Найдем связь между параметрами невозмущенного (набегающего) и адиабатно заторможенного потока газа.

Исходное уравнение:

После интегрирования при =const (в диап. и )

Отсюда получаем:

Если учесть ,что:

скорость звука ( )

число Маха

135

Полученные соотношения позволяют определить параметры заторможенного адиабатного потока, если известны соответствующие параметры невозмущенного потока.

23. Дифференциальные уравнения термодинамики

23.1. Определения

На основании первого и второго законов термодинамики устанавливаются математически строгие общие соотношения между различными свойствами любого вещества. Когда вещество претерпевает процесс, изменяются его свойства, а именно:

Функции состояния характерны тем , что их дифференциалы являются полными дифференциалами.

Если величина Z является функцией X и Y и не зависит от каких-либо других переменных, т.е.

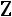
, то полный дифференциал соответствует выражению:

По свойству частных производных:

; или

Эти уравнения называются условием взаимности.

Поскольку dZ является полным дифференциалом, т.е:

- линейный интеграл

136

- интеграл по замкнутому контуру равен нулю

=0

Рассмотрим соотношение для случав когда Z=0, в этом случае dZ=0 и следовательно

Из этого уравнения для величин P, V и T получаем:

Для величин P,T и S:

Для величин I, и T:

Это все тождества.

23.2 Соотношения Максвелла

Можно выразить внутреннюю энергию и как функцию любых двух параметров состояния из четырех:. Обозначим два параметра X и Y, тогда:

137

Дифференциал выражения по Y и X соответственно и приравнивал эти вторые производные (по условию взаимности), получим:

Подставляем вместо X и Y P и S, V и S, P и T, V и T получим соотношения Максвелла.

Например, при подстановке P и S вместо X и Y:

Учитывая, что:

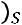
; ; ; имеет:

Для других комбинаций получим:

Соотношения Максвелла

Соотношения Максвелла играют большую роль при определении свойств веществ, поскольку в них выражена зависимость, между энтропией, давлением, объемом и температурой.

23.3 Дифференциальные уравнения для du, di, dS

Для идеального газа было:

138

Для любого вещества имеем:

Выражение для

Пусть

термическая упругость вещества

Из уравнений Максвелла

Тогда

Выражение для

Пусть тогда:

140

Из уравнения следует, что не может быть меньше поскольку всегда

отрицательно.

Для жидкости при температуре, соответствующей максимальной плотности (например вода при ):

соответственно

и

Кроме этого, из частных производных следует термодинамическое тождество:

Часть. Исследования термодинамических установок.

24. Система кпд для оценки эффективности теплоэнергетических Установок

1.Термический кпд цикла

полезная работа идеального цикла

затрачиваемая теплота от теплоотдатчика

характеризует эффективность идеального цикла (учитывает только тепло,

отданное теплоприемнику

2.Эффективный кпд

эффективная работа на валу двигателя

затраченная теплота

характеризует экономичность реального двигателя (учитывает все потери)