5.2. Подбор эмпирических формул с помощью метода наименьших квадратов.

Х	Х1	Х2	…	Хn
Y	Y1	Y2	…	Yn

Пусть мы установим зависимость между двумя величинами х и у.

Будем рассматривать х и у как прямоугольные координаты точек на плоскости. Предположим, что точки с соответствующими координатами почти лежат на некоторой прямой линии. Естественно в этом случае считать, что между х и у существует приближенная линейная зависимость, т.е. что у есть

линейная функция от х, выражающаяся формулой у=ах+b, где а и b- некоторые постоянные коэффициенты. Формулв может быть записана и в другом виде : ах+b-у=0. Т.к. точки х и у только приближенно лежат на прямой, формулы приближенные. Метод наименьших квадратов состоит в том, чтобы подобрать коэффициент а и b так, чтобы сумма квадратов погрешностей была возможно меньше: U=E₁²+E₂²+…+En²(где Е-некоторые числа не равные нулю, погрешности), если эта минимальная сумма квадратов окажется малой, тогда и сама погрешность будет малой по абсолютной величине.

Еi= ах_i+b-у_i , i=1,2,…,n

U= x_i и y_i-известные с таблицы числа. A и b- неизвестные.

Таким образом можно рассмотреть функцию двух переменных а и b. Подберем а и b так, чтобы U получило возможно меньшее значение. , . ;;;

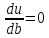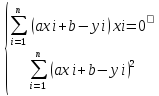6.1. Дифференциальное уравнение n-го порядка. Общее и частное решение. Задача Коши. Краевая задача.

Дифференциальные уравнения называют уравнения, связывающие между собой независимую переменную х, искомую функцию у и ее производные различных порядков по х. порядок старшей производной, входящее в данное дифференциальное уравнение, называется порядком этого уравнения. Таким образом. Общий вид Д.У. n-го порядка следующий: F(x,y,y’,y’’,…y⁽ⁿ⁾)=0

Определение 1: Общим решением дифференциального уравнения называется такое решение его у=(x, C1,C2,…,Cn) которое содержит столько независимых произвольных постоянных C1,C2,…,Cn каков порядок этого уравнения. При этом произвольные постоянные называются независимыми, если общее число постоянных, входящие в состав функции 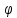, не может быть уменьшено путем введения других произвольных постоянных, непрерывно зависящих от данных.

Определение 2: всякое решение дифференциального уравнения, которое получается из общего решения, если приписать определенные значения произвольным постоянным, в него входящим, называется частным решением этого дифференциального уравнения.

Задача Коши: найти решение у= дифференциального уравнения, удовлетворяющего заданному начальному условию: у=, т.е. принимающее при х=х₀ заданное значение у=у₀. Геометрическая задача Коши формируется так: найти интегральную кривую дифференциального уравнения, проходящую через заданную точку М(х₀,у₀).

6.2. Дифференциальные уравнения первого порядка. Уравнения вида и .Уравнения с разделяющимися переменными. Однородные уравнения. Линейные дифференциальные уравнения первого порядка.

Линейным дифференциальным уравнением n-го порядка называется уравнение, в которое неизвестная функция y(x) и её производные входят линейно, т.е. в первой степени:

;

Если старший коэффициент q₀ (x) отличен от нуля на интервале (a, b), т.е. для , то, умножая (19) на , приводим уравнение к виду со старшим коэффициентом, равным 1:

;

; дальше мы будем рассматривать уравнение (20). Если правая часть уравнения тождественно равна нулю на рассматриваемом интервале (f(x)=0 при ), то уравнение называется однородным. Таким образом, однородное уравнение - это уравнение вида

;

(21)

Задача Коши для уравнений (20) и (21) ставится также, как и для общего уравнения n-го порядка (17) : требуется найти решение уравнения (20) или (21), удовлетворяющее начальным условиям

где y₀, y₁, y₂, …, y_n-1 - заданные числа. Для уравнения (17) теорема существования и единственности решения задачи Коши требовала непрерывности функции и её производных ; если привести (20) к виду (17): , то . Таким образом, условия теоремы Коши приводят к необходимости непрерывности функций f(x) и p_i(x), i = 1, 2, …, n. Далее, вывод теоремы Коши для уравнения (17) заключался в том, что найдётся окрестность точки x₀, в которой существует однозначно определённое решение задачи Коши; для линейных уравнений (20) и (21) вывод более глобален: единственное решение существует на всём интервале (a, b), на котором выполняются условия теоремы: Теорема существования и единственности решения задачи Коши для линейного уравнения: если функции f(x), p_i(x), i = 1, 2, …, n непрерывны на интервале (a, b), x₀ - произвольная точка этого интервала, то для любых начальных условий (22) существует единственная функция y(x), определённая на всём интервале (a, b) и удовлетворяющая уравнению (20) и начальным условиям (22). Всё дальнейшее изложение ведётся в предположении, что условия теоремы существования и единственности решения задачи Коши выполняются, даже если это не оговаривается специально

Однородные уравнения

Функция называется однородной степени , если для всех выполняется равенство .

Уравнение называется однородным, если правая часть является однородной функцией своих аргументов нулевой степени однородности. Однородные уравнения всегда могут быть представлены в виде

.

Предполагаем, что функция определена и непрерывна на интервале и на этом интервале функция не обращается в нуль.

Уравнение также является однородным, если однородные функции одной и той же степени однородности.

Однородные уравнения решаются посредством замены переменных:

.

Произведя такую подстановку, для новой неизвестной функции t(x) получаем уравнение

.

Полученное уравнение является уравнением с разделяющимися переменными.

Определение. Уравнение вида F(x,y,y',y'',…,y⁽ⁿ⁾) = 0, (*) связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка. Определение. Общим решением дифференциального уравнения n-го порядка называется функция у = φ(х, С₁,С₂,…,С_n), которая зависит от аргумента х и n независимых произвольных постоянных С₁, С₂, …, С_n, обращающая вместе со своими производными у', у'',…, у⁽ⁿ⁾ уравнение (*) в тождество. Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С₁, С₂, …, С_n определенные числовые значения.

14.2.1.Как следует из определения 14.1.1, обыкновенным дифференциальным уравнением первого порядка называется уравнение

;

(5)

где x - независимая переменная, y(x) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так:

;

(6)

Если пользоваться другим обозначением производной, то можно записать (6) как

;

(7)

• Общее решение (общий интеграл) уравнения при n = 1 имеет вид или . Геометрический смысл уравнения первого порядка. Уравнение (6) в каждой точке (x, y) области D, в которой задана функция f(x, y), определяет - угловой коэффициент касательной к решению, проходящему через точку (x, y), т.е. направление, в котором проходит решение через эту точку. Говорят, что уравнение (6) задаёт в D поле направлений. График любого решения дифференциального уравнения (называемый также интегральной кривой) в любой своей точке касается этого поля, т.е. проходит в направлении, определяемом полем. Интегрирование дифференциального уравнения геометрически означает нахождение кривых, у которых направление касательной в каждой точке совпадает с направлением поля. На рисунке справа изображено поле направлений, определяемое уравнением , и три интегральные кривые (три частных решения) этого уравнения. Решение можно провести через любую точку области D; единственное решение можно выделить, если задать точку, через которую проходит интегральная кривая: . Для изображения поля направлений, задаваемого дифференциальным уравнением, рассматривают линии уровня функции f(x, y), т.е. геометрические места точек, в которых касательные к интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами. С помощью изоклин можно приближённо изобразить интегральные кривые. Для примера построим изоклины уравнения . Перебираем различные значения постоянной C, строим линии уровня функции , соответствующие этим значениям С (т.е. прямые 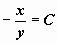), и на этих линиях ставим чёрточки в направлении, определяемым значением С (, где - угол между чёрточкой и положительным направлением оси Ох): - ось Оу; ; ; и т.д. Информация о направлении интегральных кривых, полученная из рисунка (выше справа), достаточна, чтобы сделать качественный вывод об их поведении: кривые должны огибать начало координат. Это могут быть окружности или спирали (когда мы научимся решать дифференциальные уравнения, мы легко установим, что это окружности; две такие окружности изображены пунктиром).

Уравнения с разделяющимися переменными.

---Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию

f(x) dx + g(y) dy = 0.

(10)

Пусть y(x) - решение этого уравнения, т.е. f(x)dx + g(y(x))dy(x) = 0. Интегрируя это тождество, получим - общий интеграл (общее решение) этого уравнения. ---Уравнения с разделяющимися переменными. Так называются уравнения вида

или	(11)
f1(x) g1(y) dx + f2(x) g2(y) dy = 0	(12)

Эти уравнения легко сводятся к уравнению с разделёнными переменными:

Записываем уравнение (11) в форме , затем делим на g(y) и умножаем на dx: .		Уравнение (12) делим на f2(x) g1(y): .
Эти уравнения - с разделёнными переменными. Интегрируя, получим общие интегралы:
.		.
В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному.
Если функция g(y) имеет действительные корни y1, y2, y3, …, то функции y = y1, y = y2, y = y3, …, очевидно, являются решениями исходного уравнения.		Если функция f2(x) имеет действительные корни x1, x2, x3, …, функция g1(y) имеет действительные корни y1, y2, y3, …, то функции x = x1, x = x2, x = x3, …, y = y1, y = y2, y = y3, … являются решениями исходного уравнения.
В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши.