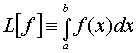13 Конечные разности

Пусть имеется таблица значений f_k функции F(x) для равноотстоящих значений аргумента x_k = x₀+k×h ( k=0, 1, 2,..,N ).

Величины

D fk= fk+1 - fk ( k=0, 1, 2,..,N-1 )

(45)

называются конечными разностями первого порядка,

D2fk =D fk+1 -D fk = fk+2 -2 fk+1 +fk (k=0, 1, 2,..,N-2)

(46)

- конечными разностями второго порядка и т.д.

Обычно конечные разности записывают в виде таблиц; например,

xk	fk	Dfk	D2fk	D3fk	D4fk
0	1	2	4	0	0
1	3	6	4	0
2	9	10	4
3	19	14
4	33

Можно показать, что отношение D^mf_k / h^k может быть принято за оценку m-й производной функции в точке x_k . Возьмем для примера m=2.

14 Разделённые разности. Интерполяционный многочлен ньютона

Разделённая разность нулевого порядка функции f(x) — сама функция f(x). Разделённая разность порядка n определяется через разделённую разность порядка n − 1 по формуле

Для разделённой разности также верна формула

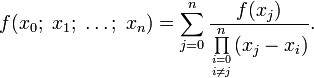
Из этой формулы следует, что разделённая разность является симметрической функцией своих аргументов (то есть при любой их перестановке не меняется), а также то, что при фиксированных разделённая разность — линейный функционал от функции f:

15 Метод наименьших квадратов

Через имеющееся "облако" точек всегда можно попытаться провести линию установленного вида, которая является наилучшей в определенном смысле среди всех линий данного вида, то есть "ближайшей" к точкам наблюдений по их совокупности. Для этого определим вначале понятие близости линии к некоторому множеству точек на плоскости. Меры такой близости могут быть различными [13]. Однако, любая разумная мера должна быть, очевидно, связана с расстоянием от точек наблюдения до рассматриваемой линии (задаваемой уравнением y=F(x)).

Предположим, что приближающая функция F(x) в точках х₁, x₂, ..., x_n имеет значения y₁, y₂, ..., y_n. Часто в качестве критерия близости используется минимум суммы квадратов разностей наблюдений зависимой переменной y_i и теоретических, рассчитанных по уравнению регрессии значений y_i. Здесь считается, что y_i и x_i - известные данные наблюдений, а F - уравнение линии регрессии с неизвестными параметрами (формулы для их вычисления будут приведены ниже). Метод оценивания параметров приближающей функции, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции, называется методом наименьших квадратов (МНК) или Least Squares Method (LS).

16 Постановка задачи численного интегрирования определение квадратурных формул

Задача численного интегрирования состоит в нахождении приближенного значения интеграла:

(4.15)

где y=f(x) - заданная функция.

Введем на отрезке [a,b] сетку :

Точки x_i называют узлами сетки (i=1, ..., N), отрезки [x_i-1,x_i] - частичными отрезками, числа h_i=x_i-x_i-1 называют шагами сетки (i=1, ..., N).

В качестве приближенного значения интеграла L[f] рассмотрим следующее:

LN[f] ≡∑ Ni=1 lN , i[f]

(4.16)

где l_i[f] - формула для приближенного вычисления интеграла 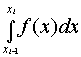на частичном отрезке [x_i-1,x_i].