
- •2 Округление приближённых чисел
- •Для того чтобы графически отделить корни уравнения (1), необходимо построить график функции . Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения
- •Теорема 1. Если непрерывная функция принимает на концах отрезка значения разных знаков, т.Е. , то на этом отрезке содержится по крайней мере один корень уравнения (1)
- •6Методы половинного деления
- •7 Метод простых итераций решения уравнения
- •Сходимость метода простых итераций
- •8 Метод гаусса решения систем линейных уравнений
- •9 Норма вектора. Сходимость по норме виды норм вектора
- •10 Норма матрици. Виды норм матрици согласованной с нормой вектора Норма матрицы
- •13 Конечные разности
- •14 Разделённые разности. Интерполяционный многочлен ньютона
- •15 Метод наименьших квадратов
- •16 Постановка задачи численного интегрирования определение квадратурных формул
7 Метод простых итераций решения уравнения
Пусть задана нелинейная непрерывная функция действительного переменного f(x) на отрезке [a,b]R. Требуется решить уравнение
f(x)=0 (1)
Метод простой итерации состоит в том, что уравнение (1) заменяем на основе равносильных преобразований уравнением вида
x=(x) (2)
а затем строим
последовательность приближений
![]() к
корню уравнения x*по
правилу
к
корню уравнения x*по
правилу
![]() (3)
(3)
Здесь k-номер
итерации. Приближенное значение корня
с нулевым индексом, т.е.
![]() называют
начальным приближением. Это значение
выбирается из каких-либо условий
конкретной задачи или берется произвольно.
Подставляем это значение в правую часть
соотношения (3) и получаем
называют
начальным приближением. Это значение
выбирается из каких-либо условий
конкретной задачи или берется произвольно.
Подставляем это значение в правую часть
соотношения (3) и получаем
![]() ,
затем вычисленное таким образом каждое
очередное приближение подставляем в
правую часть и получаем
,
затем вычисленное таким образом каждое
очередное приближение подставляем в
правую часть и получаем
![]()
В итоге получаем
числовую последовательность
![]() ,которая
называется последовательностью
приближений или итерационной
последовательностью.
,которая
называется последовательностью
приближений или итерационной
последовательностью.
Сходимость метода простых итераций
Метод сходится,
если при
![]() последовательность
{
последовательность
{![]() }
имеет предел.
Обозначим
}
имеет предел.
Обозначим
![]() окресность
точки
окресность
точки
![]() радиуса
радиуса
![]() ,
то есть
,
то есть
![]() .
Теорема
1. Если
.
Теорема
1. Если
![]() липшиц-непрерывна
с константой
липшиц-непрерывна
с константой
![]() на
на
![]() ,
то есть выполняется
,
то есть выполняется
![]() ,
,
при этом если также выполнено
![]() ,
,
то уравнение
![]() имеет
единственное решение на
имеет
единственное решение на
![]() и
метод простой итерации сходится к
решению при любом выборе начального
приближения
и
метод простой итерации сходится к
решению при любом выборе начального
приближения
![]() .Так
же справедлива оценка:
.Так
же справедлива оценка:
![]() ,
,
где
![]() -
точное решение.
Из оценки видно, что
метод линеен. Пусть
-
точное решение.
Из оценки видно, что
метод линеен. Пусть
![]() непрерывно
дифференцируема на
непрерывно
дифференцируема на
![]() ,
тогда из теоремы вытекают следующие
утверждения:
Следствие
1. Если
,
тогда из теоремы вытекают следующие
утверждения:
Следствие
1. Если
![]() для
для
![]() ,
выполнено
,
выполнено
![]() ,
и
,
и
![]() ,
тогда уравнение
,
тогда уравнение
![]() имеет
единственное решение на
имеет
единственное решение на
![]() и
метод простой итерации сходится к
решению.
Следствие
2. Если
уравнение
и
метод простой итерации сходится к
решению.
Следствие
2. Если
уравнение
![]() имеет
решение
имеет
решение
![]() ,
,
![]() непрерывно
дифференцируема на
непрерывно
дифференцируема на
![]() и
и
![]() .
Тогда существует
.
Тогда существует
![]() такое,
что на
такое,
что на
![]() уравнение
не имеет других решений и метод простой
итерации сходится к решению при
уравнение
не имеет других решений и метод простой
итерации сходится к решению при
![]()
8 Метод гаусса решения систем линейных уравнений
Метод Гаусса - классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
9 Норма вектора. Сходимость по норме виды норм вектора
Линейное пространство называют нормированным, если
каждому его вектору x поставлено в соответствие число,
называемое нормой и обозначаемое как ||x||.
Аксиомы нормированного пространства:
1. | x||≥ 0, причем ||x||0 x 0.
2. ||x + y|| ≤ ||x|| + ||y||
3. || x|| ≤ | | ||x||
10 Норма матрици. Виды норм матрици согласованной с нормой вектора Норма матрицы
Нормой матрицы
A
называется вещественное
число
![]() ,
удовлетворяющее первым
трём из
следующих условий:
,
удовлетворяющее первым
трём из
следующих условий:
-
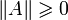 ,
причём
,
причём
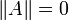 только
при
только
при
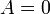 ;
; -
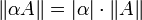 ,
где
,
где
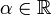 ;
; -
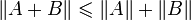 ;
; -
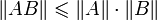 .
.
Если выполняется также и четвёртое свойство, норма называется мультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы мультипликативны. Немультипликативные нормы для матриц являются простыми нормами, заданными в линейных пространствах матриц.
