- •Взаимное расположение двух прямых
- •2. Для построения фронтального следа n прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.
- •Способ вращения.
- •Способ перемены плоскостей проекций.
- •1. Сечение поверхности цилиндра
- •Метод секущих плоскостей
2. Для построения фронтального следа n прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.
|
|
|
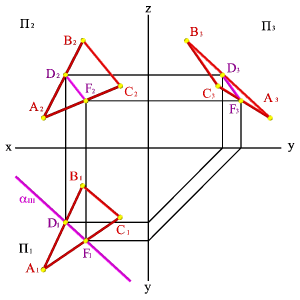
С помощью этих правил найдены на эпюре следы прямой а (рис.27) . Здесь же показаны совпавшие проекции точки А, принадлежащей рассматриваемой прямой. Особенность этой точки в том, что она равноудалена от плоскостей проекций, то есть находятся в биссекторной плоскости 2бис. Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.
|
|
|
Рисунок 27. Нахождение горизонтального и фронтального следов прямой линии |
|||
Билет №10

Положение плоскости в пространстве определяется (рис.3.1): тремя точками, не лежащими на одной прямой (1), прямой и точкой, взятой вне прямой(2), двумя пересекающимися прямыми (3) , двумя параллельными прямыми (4), геометрической фигурой (5), следами плоскости (6).
Следы плоскости !
Следом плоскости называется линия пересечения плоскости с плоскостью проекций. В зависимости, от того с какой из плоскостей проекций пересекается данная плоскость, различают: горизонтальный, фронтальный и профильный следы плоскости.
Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой (как для построения любой прямой). На рисунке 52 показано нахождение следов плоскости α(АВС). Фронтальный след плоскости αП2 построен, как прямая соединяющая две точки N(АС) и N(АВ), являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α. Горизонтальный следαП1 – прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след αП3 – прямая соединяющая точки (αy и αz) пересечения горизонтального и фронтального следов с осями. Точки αx, αy и αz называют точками схода следов.
|
|
|
|
|
|
Билет №11
Плоскость
относительно плоскостей проекций
может занимать следующие
положения:
1
- не перпендикулярно к плоскостям
проекций;
2 -
перпендикулярно к одной плоскости
проекций;
3 -
перпендикулярно к двум плоскостям
проекций.
Плоскость,
не перпендикулярную данным плоскостям
проекций, называют плоскостью общего
положения (рис.3.6).
Во втором и третьем случаях плоскости
называют плоскостями частного
положения.
Плоскость,
перпендикулярная одной плоскости
проекций.
Такие
плоскости получили название проецирующих
плоскостей. Горизонтально проецирующей
плоскостью называют плоскость,
перпендикулярную к плоскости
проекций П1 (рис.3.7).
Любой
элемент, лежащий в этой плоскости,
проецируется на плоскость П1 в
прямую Г1,
называемую горизонтальным следом
плоскости. Угол наклона горизонтально
проецирующей плоскости к плоскости
проекций П2 на
комплексном чертеже определяется
как угол 1,
заключенный между горизонтальным
следом Г1 данной
плоскости и прямой, перпендикулярной
линиям связи (рис.3.7-б).
Фронтально
проецирующей плоскостью (рис.3.8)
называют плоскость, перпендикулярную
к плоскости проекций П2.
Любой элемент этой плоскости
проецируется на фронтальную плоскость
проекций в прямую Ф2 -
фронтальный след плоскости. Угол
наклона фронтально
проецирующей плоскости к плоскости П1 на
комплексном чертеже определяется
как угол 2,
заключенный между фронтальным
следом Ф2 и
прямой, перпендикулярной линиям
связи.
Профильно проецирующей плоскостью
называют плоскость, перпендикулярную
к профильной плоскости проекций
(рис.3.9). Любой элемент, лежащий в этой
плоскости, проецируется на профильную
плоскость проекций в прямую 3 -
профильный след плоскости. На профильной
проекции углы и наклона
профильно проецирующей плоскости к
плоскостям П2 и П2изображаются
без искажения.
Свойство
проекций геометрических элементов,
лежащих в проецирующих плоскостях
(см. 2.1).
Проецирующая
плоскость изображается прямой линией
на той плоскости проекций, к которой
она перпендикулярна. Следовательно,
и любая геометрическая фигура, лежащая
в проецирующей плоскости, проецируется
на эту плоскость в отрезок прямой.
Проецирующие
плоскости могут быть заданы не только
геометрическими элементами, лежащими
в данной плоскости, но и одной линией
- следом плоскости (рис.3.10). Например,
горизонтально проецирующая
плоскость Г может
быть задана своим горизонтальным
следом Г1.
Аналогично, фронтально проецирующая
плоскость может быть задана своим
фронтальным следом Ф1.
Плоскость,
перпендикулярная двум плоскостям
проекций.
Плоскости, перпендикулярные двум
плоскостям проекций, параллельны
третьей плоскости и называются
плоскостями уровня или дважды
проецирующими плоскостями.
Различают три плоскости уровня:
горизонтальную плоскость уровня
(рис.3.11-а) - параллельную П1;
фронтальную плоскость уровня (рис.
3.11-6) - параллельную П3;
профильную плоскость уровня (рис.3.11-в)
- параллельную П3.
Любая линия (прямая или кривая),
принадлежащая плоскости уровня,будет
являться линией уровня. Любая фигура,
лежащая в плоскости уровня, проецируется
без искажения на плоскость проекций,
ей параллельную.
|
|||
|
|
|||
|
Билет №12 |
Плоскость перпендикулярная профильной плоскости ( П3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость
|
|
|
|
а) модель |
б) эпюр |
|
Рисунок 5.8. Биссекторная плоскость |
|
В общем случае круговая коническая поверхность включает в себя две совершенно одинаковые полости, которые имеют общую вершину. Образующие одной полости представляют собой продолжение образующих другой полости. На практике мы имеем дело не с бесконечно расширяющимися двумя полостями конической поверхности, а с телом, которое ограничено одной полостью этой поверхности и плоскостью, что является обычным круговым конусом.
Билет №13
Прямая АВ принадлежит плоскости α, если две ее точки А и В принадлежат этой плоскости α. (ΔКLM) Справедливо и обратное утверждение: если точки А и В принадлежат плоскости α ( (ΔКLM), то пряма АВ, проходящая через эти точки, принадлежит плоскости α.
Прямые АВ и CD, принадлежащие разным плоскостям показаны на рис. 3. 7. Прямая АВ принадлежит плоской фигуре LKM, потому что на проекциях прямой и плоской фигуры имеются две общих точки. Прямая CD принадлежит плоскости, заданной параллельными прямыми с и d, т. к. она проходит через точки С и D, расположенные на этих прямых.
Прямая принадлежит плоскости, если ее следы принадлежат одновременно следам плоскости.
Справедливо и обратное утверждение: если следы прямой принадлежат следам плоскости, то эта прямая принадлежит плоскости.
Кроме того, существует еще одно свойство, определяющее взаимное положение точки и плоскости: точка принадлежит плоскости, если она расположена на прямой, принадлежащей этой плоскости (рис. 3.7).
 .
.
а
 .
.
б
Билет №14
Среди прямых линий, принадлежащих плоскости, особое значение имеют прямые, занимающие частное положение в пространстве:
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (h АВС h hОх,h Оy)(рис.55).
|
|
|
|
|
|
|
|
||||
|
|
||||
|
|
||||
|
а) модель |
б) эпюр |
|||
|
Рисунок 55. Горизонталь |
||||
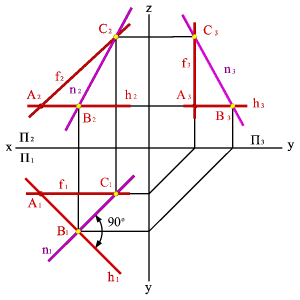
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fАВС f fОх, f Оz)(рис.56).
|
|
|
|
|
|
|
|||
|
|
|||
|
|
|||
|
|
|
||
|
Рисунок 56. Фронталь |
|||
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (рАВС р р1Ох,рОх) (рис.57).
|
|
|
|
|
|
|
|
||||
|
|
||||
|
|
||||
|
а) модель |
б) эпюр |
|||
|
Рисунок 57. Профильная прямая |
||||
Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.
4. Прямые, принадлежащие плоскости и образующие с плоскостью проекций наибольший угол называются линиями наибольшего наклона данной плоскости к плоскости проекций. С помощью линий наибольшего наклона определяют двугранные углы между заданной плоскостью и соответствующей плоскостью проекций.
Прямые плоскости, перпендикулярные соответствующим линиям уровня являются линиями наибольшего наклона.
Линия наибольшего наклона к горизонтальной плоскости проекций называется линией ската. Такое название объясняется тем, что эта линия является траекторией, по которой шарик скатывается с данной плоскости. По отношению к плоскостям П2 и П3 целесообразнее употреблять название линия наибольшего наклона.
Линия ската и её горизонтальная проекция образуют линейный угол , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.58). Горизонтальная проекция линии ската плоскости общего положения перпендикулярна горизонтальной проекции горизонталь этой плоскости. Фронтальная и профильная проекции ската строятся по её принадлежности плоскости.
|
|
|
|
|
|
|
|||
|
|
|||
|
|
|||
|
|
|
||
Билет №15
Линией наибольшего ската плоскости γ называется прямая g, принадлежащая этой плоскости и перпендикулярная ее линиям уровня: горизонтали h и фронтали f (рис.4.9).
 .
.
Рис. 4.8. Определение длины отрезка и углов наклона к плоскостям проекций
 .
.
Рис. 4.9. Пример построения линии наибольшего наклона
На комплексном чертеже горизонтальная проекция линии наибольшего наклона перпендикулярна горизонтальной проекции горизонтали этой плоскости, а фронтальная − фронтальной проекции фронтали.
Главным свойством этой линии наибольшего ската является то, что она образует с горизонтальной плоскостью проекций π1 угол α°, равный углу наклона плоскости γ к плоскости π1.
Это свойство линии наибольшего наклона (ската) используется для определения углов наклона плоскостей к плоскостям проекций.
Билет №16
Для построения прямой , проходящей через заданную точку пространства параллельно заданной плоскости, достаточно провести прямую, параллельную любой прямой , принадлежащей плоскости. При этом возможно бесчисленное множество решений.
Дополнительные требования могут обусловить единственное решение. Для того чтобы проверить, параллельна ли прямая заданной плоскости, можно попробовать провести в этой плоскости прямую , параллельную заданной. Если такую прямую в плоскости построить не удается, то заданная прямая и плоскость не параллельны между собой. Можно также попытаться найти точку пересечения данной прямой с данной плоскостью. Если такая точка не может быть найдена, то заданные прямая и плоскость взаимно параллельны.

Билет №17
Прямая пересекает плоскость в одной точке. Точку пересечения прямой с плоскостью определяют путем построения вспомогательной прямой линии, лежащей в одной проецирующей плоскости с заданной прямой. На рис. 119, а приведен комплексный чертеж прямой l и плоскости 9 (ABC), причем т ~ Q (ABC). Через горизонтальную проекцию прямой l1 проводим проекцию вспомогательной горизонтально проецирующей плоскости Sum1. В пересечении плоскостей Q и Sum получаем линию т, то есть т =Sum ^ Q. Горизонтальная проекция прямой т определяется горизонтальными проекциями точек 1 и 2 пересечения линий ЕС и АС со вспомогательной плоскостью Sum , то есть В1С1 ^ Sum =l1; А1С1 ^ Sum1=21; т1 = l1^21.

Рис. 119

Рис. 120

Рис. 121
Для получения фронтальной проекции линии l построим фронтальные проекции точек 1 и 2, соединив которые, получим фронтальную проекцию m2. В пересечении фронтальных проекций прямых т и l получим фронтальную проекцию точки К, принадлежащей и прямой l, и прямой т, лежащей в плоскости Sum. Значит, точка К и принадлежит плоскости Sum, и является точкой пересечения прямой l с плоскорью Sum.
Видимость прямой и плоскости относительно горизонтальной плоскости проекций определяется с помощью горизонтально конкурирующих точек 2 и 3, а видимость относительно фронтальной плоскости проекции — с помощью фронтально конкурирующих точек 3 и 4.
Если плоскость занимает частное положение, то одна проекция точки пересечения прямой с плоскостью определяется сразу в пересечении вырожденной проекции плоскости с соответствующей проекцией прямой (рис. 119, б).
Если прямая пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня плоскости на основании теоремы о проецировании прямого угла (см. § 29).
На рис. 120 построены проекции основания М перпендикуляра п, проведенного к плоскости 9 (ABC) из точки К пространства. В AВС имеем: АВ — горизонталь (A2B2 _|_ A2A1), AC — фронталь (А1С1 _|_A1A2). Поэтому проекции перпендикуляра n э К располагаются: п1 _|_A1B1 и n2 _|_ А2С2. Основание перпендикуляра на плоскости построено с помощью вспомогательной линии а плоскости, лежащей в одной с перпендикуляром п горизонтально проецирующей плоскости (а ^ п = М).
Если прямая пересекает плоскость в бесконечности, то имеет место параллельность прямой с плоскостью. На рис. 121 построена прямая т, проходящая через точку N uпараллельная плоскости треугольника KLM. На комплексном чертеже параллельность прямой и плоскости доказывается тем, что т1 || а1 и m2 || а2; a ~ KLM.
Билет №18
Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.
Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.
Пусть прямая n, перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию n перпендикулярна любой прямой плоскости. Проведем в плоскости BCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n1h1. Аналогично для фронтали – fn f2 n2.
Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.
Доказательство следует из теоремы о проецировании прямого угла.
Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А (рис.61).
Задача. Дано: плоскость ВСD и точка А.
Требуется построить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD.
В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А1 прямую n1 перпендикулярно горизонтальной проекции горизонтали h1, а на фронтальной плоскости проекций через точку А2 прямую n2 перпендикулярно фронтальной проекции фронтали f2, согласно, теореме о перпендикуляре к плоскости, полученная прямая n будет перпендикулярна плоскости ВСD.
|
|
|
|
|
||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|
||||||
|
Билет №19
|
|||||||
Билет №20
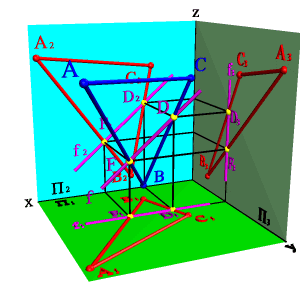
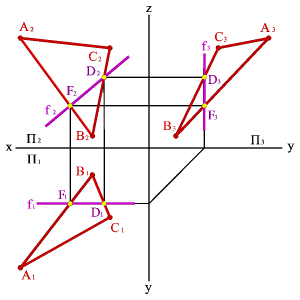
Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.
Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.64).
Задача. Дано: плоскость общего положения, заданная треугольником АВС, а вторая плоскость - горизонтально проецирующая .
Требуется построить линию пересечения заданных плоскостей.
Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью - точка D, прямой(AС) -F. Отрезок DF определяет линию пересечения плоскостей. Так как - горизонтально проецирующая плоскость, то проекция D1F1 совпадает со следом плоскости П1 таким образом остается только построить недостающие проекции DF на П2 и П3.
|
|
|
|
|
|
|
|
||||
|
|
||||
|
|
||||
|
а) модель |
б) эпюр |
|||
|
Рисунок 64. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью |
||||
Рассмотрим общий случай пересечения плоскостей, когда плоскости занимают общее положение в пространстве.
Задача. Дано: Две плоскости общего положения m,n) и (ABC) (рис.65).
Требуется построить линию пересечения плоскостей и .
|
|
|
|
|
|
|
|
||||
|
|
||||
|
|
||||
|
|
|
|||
|
|
||||
Рассмотрим последовательность построения линии пересечения плоскостей (m//n) и (АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости и . Найдем линии пересечения этих плоскостей с заданными плоскостями. Плоскость пересекает плоскость по прямой (12), а плоскость - по прямой (34). Точка пересечения этих прямых - К, котораяодновременно принадлежит трем плоскостям , и , т.е. искомой линии пересечения плоскостей и . Плоскость пересекает плоскости и по прямым (56) и (7C), точка их пересечения М расположена одновременно в трех плоскостях , , и принадлежит прямой линии пересечения плоскостей и . Таким образом, прямая (КМ) является линией пересечения плоскостей и .
Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость. В этом случае точки, определяющие положение линии пересечения плоскостей, находятся как точки пересечения прямой и плоскости.
Билет №21
Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку Аможно провести множество плоскостей перпендикулярных данной плоскости (f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость . Для того чтобы из точки А провести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямыми hf необходимо из точки Апровести прямую n перпендикулярную плоскости hf (горизонтальная проекция n перпендикулярна горизонтальной проекции горизонтали h, фронтальная проекция n перпендикулярна фронтальной проекции фронтали f). Любая плоскость проходящая через прямую n будет перпендикулярна плоскости hf, поэтому для задания плоскости через точки А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми mn будет перпендикулярна плоскости hf
|
|
|
Перпендикулярность плоскостей. Две плоскости называются взаимно перпендикулярными, если угол между ними равен 90∘. Если плоскости α и β взаимно перпендикулярны, то пишут α⊥β .
Признак перпендикулярности плоскостей: Если плоскость содержит перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости.
Теорема о взаимно перпендикулярных плоскостях. Если две плоскости взаимно перпендикулярны, то прямая, принадлежащая одной плоскости и перпендикулярная линии пересечения плоскостей, перпендикулярна другой плоскости.
Билет №22


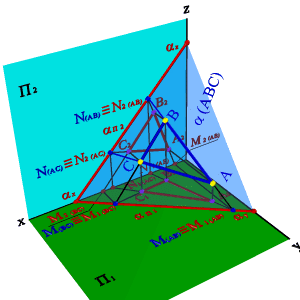

 Рис.
3.7-а
Рис.
3.7-а  Рис.
3.7-б
Рис.
3.7-б Рис.
3.8-а
Рис.
3.8-а  Рис.
3.8-б
Рис.
3.8-б Рис.
3.9.
Рис.
3.9. Рис.
3.10.
Рис.
3.10. Рис.
3.11-а,б
Рис.
3.11-а,б  Рис.
3.11-в
Рис.
3.11-в







 Доказательство
Пусть
α и β - данные плоскости, a1 и a2 –
прямые в плоскости α, пересекающиеся
в точке A, b1 и b2 – соответственно
параллельные им прямые в плоскости
β.
Предположим,
что плоскости α и β не параллельны,
а значит пересекаются по некоторой
прямой с. По теореме о признаке
параллельности прямой и плоскости
прямые a1 и a2, как параллельные
прямые b1 и b2, параллельны плоскости
β, и поэтому они не пересекают
лежащую в этой плоскости прямую
с. Таким образом, в плоскости α
через точку A проходят прямые a1
и a2, параллельные прямой с. Это
невозможно по аксиоме параллельных.
Что противоречит предположению.
Теорема доказана.
Доказательство
Пусть
α и β - данные плоскости, a1 и a2 –
прямые в плоскости α, пересекающиеся
в точке A, b1 и b2 – соответственно
параллельные им прямые в плоскости
β.
Предположим,
что плоскости α и β не параллельны,
а значит пересекаются по некоторой
прямой с. По теореме о признаке
параллельности прямой и плоскости
прямые a1 и a2, как параллельные
прямые b1 и b2, параллельны плоскости
β, и поэтому они не пересекают
лежащую в этой плоскости прямую
с. Таким образом, в плоскости α
через точку A проходят прямые a1
и a2, параллельные прямой с. Это
невозможно по аксиоме параллельных.
Что противоречит предположению.
Теорема доказана.