Билет №1

«Начертательная геометрия – раздел геометрии, в котором пространственные фигуры, а также методы решения и исследования пространственных задач изучаются с помощью их изображений на плоскости».

Методы начертательной геометрии являются теоретической базой для решения задач технического черчения. В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне исследовать предметы и их отдельные детали. Для того чтобы правильно выразить свои мысли с помощью рисунка, эскиза, чертежа требуется знание теоретических основ построения изображений геометрических объектов, их многообразие и отношения между ними, что и составляет предмет начертательной геометрии.

Изображение фигуры на плоскости как графический способ представления информации о ней имеет преимущества в сравнении с другими способами:

– общение становится более доступным, потому что образы, создаваемые на основе визуального (зрительного) восприятия, обладают большей, чем слова, ассоциативной силой;

– изображения являются интернациональным языком общения, тогда как, например, вербальное общение требует для понимания, как минимум знания языка собеседника.

Таким образом теоретические основы визуализации информации о геометрических объектах, многообразие геометрических объектов пространства, отношения между ними и их графического отображения на плоскости составляют предмет начертательной геометрии.

Задача этой науки – создание оптимальных геометрических форм объектов машиностроения, архитектуры и строительства, разработка теории графического отображения объектов и процессов.

Начертательная геометрия со времен ее основоположника Г. Монжа (1746-1818)  завоевала свое достойное место в высшей школе как наука. Важнейшее прикладное значение начертательной геометрии как учебной дисциплины состоит в том, что она учит владеть графическим языком, выполнять и читать чертежи и другие изображения геометрических объектов, без чего немыслимо формирование инженера. Она обеспечивает преемственность между школьными курсами геометрии и черчения и графическими дисциплинами вуза.

Изучение начертательной геометрии способствует развитию пространственного воображения и навыков правильного логического мышления. Совершенствуя нашу способность - по плоскому изображению мысленно создавать представления о форме предмета и наоборот создание изображений мысленно созданных образов – визуализация мысли.

Однако не всякое изображение отображает геометрические свойства оригинала и не может быть принято для всестороннего его исследования. Принципиальное отличие методов изображения, изучаемых в курсе начертательной геометрии, от некоторых современных технических средств отображения (фотография, голография и др.), заключается в возможности с большой наглядностью и метрической достоверностью отобразить не только существующие предметы, но и возникающие в нашем представлении образы проектируемого объекта.

Изображение, которое позволяет определять взаимосвязь (взаимопринадлежность) элементов объекта, называют полным.

Изображения, по которым можно определить размеры объекта, называется метрически определенными.

Из плоскостных изображений объекта наиболее широкое применение в практике получили рисунки и чертежи. Рисунком называют изображение предмета от руки и на глаз с кажущимися относительными размерами и положениями отдельных его элементов. Чертежом называют изображение предмета, построенное по особым правилам с помощью чертежных инструментов в точной зависимости от размеров и положения в пространстве соответствующих линий предмета.

В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне, исследовать предметы и их отдельные детали.

Эти требования к чертежам и привели к созданию теории изображений, составляющей основу начертательной геометрии. Правила построения изображений основаны на методе проекций. Поэтому проекционный метод построения изображений является основным методом начертательной геометрии

Итак, в курсе начертательной геометрии изучаются:

1. методы отображения пространственных объектов на плоскости;

2. способы графического и аналитического решения различных геометрических задач;

3. приемы увеличения наглядности и визуальной достоверности изображений проецируемого объекта;

4. способы преобразования и исследования геометрических свойств изображенного объекта;

5. основы моделирования геометрических объектов.

Билет №2

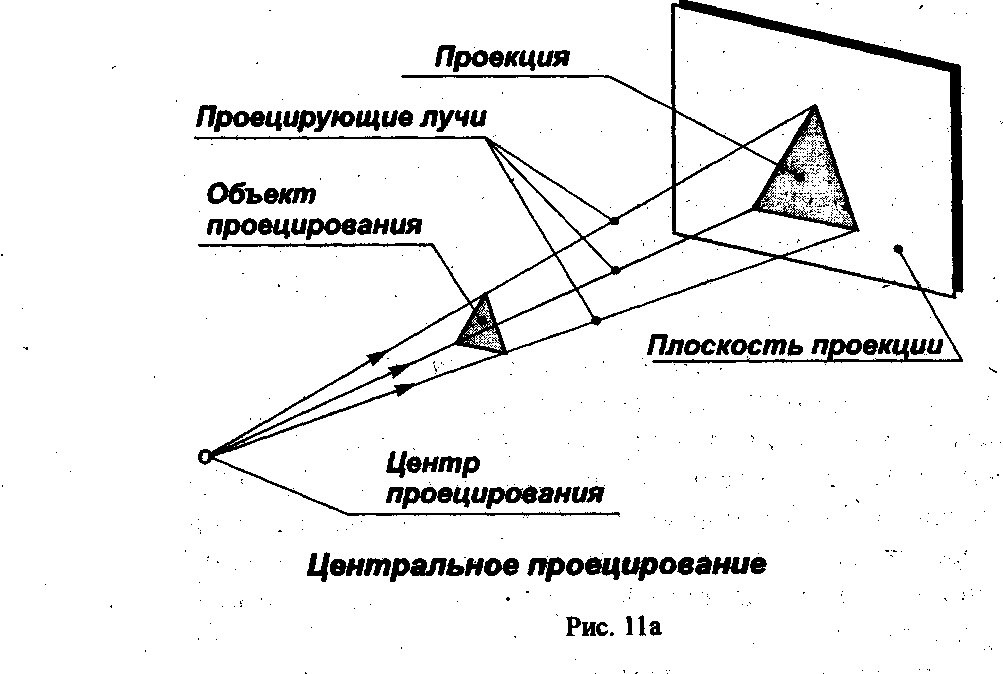
Проецирование - это процесс полу­чения изображения предмета на какой-либо поверх­ности Получившиеся при этом изображение называют проекцией предмета Нечто похожее на проекцию можно наблюдать, если параллельно стене, противопо­ложной окну, расположить ученическую тетрадь. На сте­не образуется тень в виде прямоугольника. Элементами, с помощью которых осуществляется проецирование, являются (рис. 11): центр проецирова­ния - точка, из которой производится проецирование; объект проецирования - изображаемый предмет; плоскость проекции - плоскость, на которую производится проецирование;проецирующие лучи - воображаемые прямые, с помощью которых производится проецирова­ние, результатом проецирования является изображение, или проекция, объекта. Различают центральное и параллельное проеци­рование. При центральном проецировании все проеци­рующие лучи исходят из одной точки - центра проеци­рования, находящегося на определённом расстоянии от плоскости проекций. На рис, 11а за центр проециро­вания условно взята электрическая лампочка. Исходящие от неё световые лучи, которые условно приняты за про­ецирующие, образуют на полу тень, аналогичную цен­тральной проекции предмета. Метод центрального проецирования используется при построении перспективы. Перспектива даёт возмож­ность изображать предметы такими, какими они пред­ставляются нам в природе при рассмотрении их с опре­делённой точки наблюдения. В машиностроительных чертежах центральные проекции не применяются. Ими пользуются в строитель­ном черчении и в рисовании. При параллельном проецировании все проеци­рующие лучи параллельны между собой. На рис.11б по­казано, как получается параллельная косоугольная про­екция. Центр проецирования предполагается условно удалённым в бесконечность. Тогда параллельные лучи отбросят на плоскость проекций тень, которую можно принять за параллельную проекцию изображаемого предмета. В черчении пользуются параллельными проекция­ми. Выполнять их проще, чем центральные. Если проецирующие лучи составляют с плоскостью проекций примой угол, то такие параллельные проекции называются прямоугольными. Прямоугольные проекции называют также ортого­нальными. Слово "ортогональный" происходит от гре­ческих слов "orthos" - прямой и "gonia" - угол. Чертежи в системе прямоугольных проекций дают достаточно полные сведения о форме и размерах предмета, так как предмет изображается с нескольких сторон. Поэтому в производственной практике пользуются чертежами, со­держащими одно, два, три или более изображений пред­мета, полученных в результате прямоугольного проеци­рования. Аксонометрические проекции Чертёж, выполненный в прямоугольных (ортого­нальных) проекциях, является основным видом изобра­жения, которым пользуются в технике. Для облегчения пространственного представления о предмете иногда применяют аксонометрические проекции. Аксонометри­ческие проекции передают одним изображением про­странственную форму предмета. Такое изображение соз­даёт у человека впечатление, близкое к тому, которое получается при рассмотрении предмета в "натуре". Ак­сонометрические проекции получаются, если изобра­жаемый предмет вместе с осями координат, к которым он отнесён, с помощью параллельных лучей проецируют на одну плоскость, называемойаксонометрической. Слово "аксонометрия" переводится "измерение по осям или измерения параллельно осям", так как размеры изображаемого предмета откладываются параллельно осям х, у, z называемым аксонометрическими осями. В зависимости от наклона осей координат х, у, z к аксо­нометрической плоскости и угла, составляемого проецирующими лучами с этой плоскостью, образуются раз­личные аксонометрические проекции. Если проецирую­щие лучи перпендикулярны плоскости, то проекция на­зывается прямоугольной. Если проецирующие углы наклонны к плоскости, то проекция называется косо­угольной. 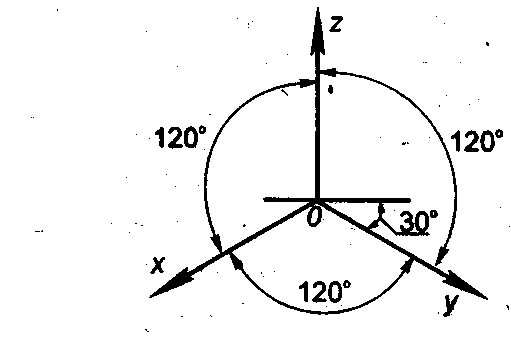Фронтальная диметрическая проекция Во фронтально диметрической проекции аксоно­метрические оси х, у, zрасполагаются следующим обра­зом: ось х расположена горизонтально; ось zвертикаль­но; ось у проходит под углом 45 к горизонтальной оси. По направлению осей х, z откладываются истин­ные величины размеров предмета. Размеры по оси у и направлениям, ей параллельным, со­кращают наполовину.   Прямоугольная изометрическая проекция Расположение осей х, у, z в изометрической про­екции следующее Ось zпроводят вертикально, а оси х и у — под углом 30 к го­ризонтали. При вычерчивании изометриче­ской проекции размеры по всем трём осям от­кладывают без сокра­щения, то есть натуральные

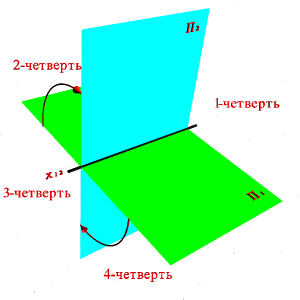
Билет №3 Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Гаспаром Монжем - крупным французским геометром конца 18, начала  19 веков, 1789-1818 гг. одним из основателей  знаменитой политехнической школы в Париже и участником работ по введению метрической системы мер и весов. Постепенно накопившиеся отдельные правила и приемы таких изображений были приведены в систему и развиты в труде Г. Монжа "Geometriedescriptive". Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей. В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.6). Одну из плоскостей проекций П1   располагают горизонтально, а вторую П2 - вертикально. П1 - горизонтальная плоскость проекций, П2- фронтальная. Плоскости бесконечны и непрозрачны. Плоскости проекций делят  пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций. Линия пересечения плоскостей проекций называется осью координат  и обозначается x12. Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти. Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2 (рис.6). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром Монжа (франц. Epure – чертеж.) или комплексным чертежом. Геометрические объекты делятся на: линейные (точка,прямая,плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы). Рассмотрим способы их образования, графического задания и возможные варианты положения по отношению к плоскостям проекций. Рисунок 6. Пространственная модель двух плоскостей проекций

Билет №4

Относительно плоскостей проекций прямая может занимать различные положения:

• Не параллельна ни одной из плоскостей проекций П₁, П₂, П₃.

• Параллельна одной из плоскостей проекций ( прямая может и принадлежать этой плоскости);·

• Параллельна двум плоскостям проекций, т.е. перпендикулярна третьей.

Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения ( см. рис. 2.3, 2.4) .(следствие 1). Прямую, параллельную одной из плоскостей проекций или двум плоскостям проекций, т. е. перпендикулярную третьей, называют прямой частного положения.

На рисунке 2.5 приведены наглядные изображения и чертежи отрезков прямых частного положения - параллельных плоскостям проекции: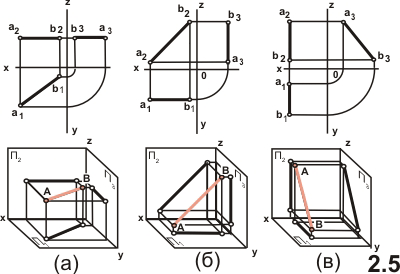

a) Прямая АВ параллельна плоскости П₁ ( ее называют горизонтальной прямой - горизонталь); фронтальная проекция a₂b₂ параллельна оси x; длина горизонтальной проекции равна длине самого отрезка(a₁b₁ =AB);

b) Прямая АВ параллельна плоскости П₂ ( ее называют фронтальной прямой - фронталь); горизонтальная проекция a₁b₁ параллельна оси x; длина фронтальной проекции отрезка равна длине самого отрезка (а₂b₂=AB);

c) Прямая АВ параллельна плоскости П₃( ее называют профильной прямой - профиль); длина профильной проекции отрезка равна длине самого отрезка (a₃b₃= AB) ;

Эти прямые называют прямыми уровня ( следствие 2).

На рисунке 2.6 приведены чертежи отрезков прямых, перпендикулярных плоскостям проекций: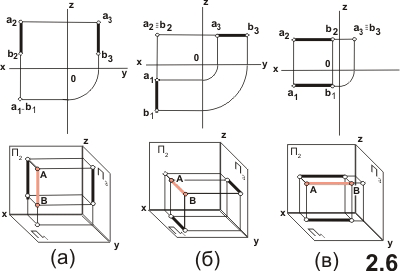

a) Прямая перпендикулярна плоскости П₁, ее проекция a₂b₂ перпендикулярна оси x; проекции а₁ и b₁ совпадают;

b) Прямая перпендикулярна плоскости П₂, ее проекция a₁b₁ перпендикулярна оси x, проекции a₂ и b₂ совпадают;

c) Прямая перпендикулярна плоскости П₃, ее проекции a₁b₁, a₂b₂ параллельны оси x; проекции a₃ и b₃ совпадают;

Эти прямые называют проецирующими ( следствие 3).

Как уже указывалось, если точка принадлежит прямой, то ее проекции принадлежат одноименным проекциям этой прямой ( см. рис. 2.3 , 2.4) . Обратное положение: если две проекции точки принадлежат одноименным с ними проекциям прямой в системе П₁, П₂, то точка принадлежит прямой, - справедливо для проекций всех прямых, кроме профильной. Для профильных прямых обратное положение справедливо только в системах П₁, П₂, П₃, или П₂, П₃, или П₁, П₃.

Билет №5

Определить длину отрезка AВ и угол его наклона к плоскости проекций можно способом введения новых плоскостей проекций. Если отрезок общего положения параллелен какой-либо плоскости, то очевидно, что он проецируется на нее в натуральную величину. Поэтому для решения этой задачи нам нужно ввести дополнительную плоскость проекций П₄ так, чтобы она была параллельна нашему отрезку. Плоскость П₄ может быть перпендикулярной к П₁ либо П₂, от этого зависит лишь угол наклона к какой плоскости проекций мы сможем определить. На рисунке П₄ перпендикулярна П₁.

Нажмите на картинку для просмотра...

Алгоритм графических построений: Проводим ось проекций П1П4 параллельно A1B1 и на произвольном расстоянии от A1B1; Проводим линии проекционной связи в системе плоскостей проекции П1П4 перпендикулярно оси П1П4; Откладываем на них от оси П1П4 расстояния равные расстояниям от А2 и B2 до оси П1П2; Соединяем А4 и B4.  Длина проекции А4B4 равна длине отрезка АВ. Угол  - угол наклона А4B4 к оси П1П4 равен углу наклона АВ к плоскости проекции П1.

 Если нам требуется найти угол наклона отрезка AB к плоскости П₂, то дополнительную плоскость проекций П₄ следует вводить перпендикулярно П₂. Все построения аналогичны, только выполняются они в верхней части чертежа. Естественно, что искомая длина отрезка AB будет одинакова в обоих случаях.

Билет №6

В пространстве точка и прямая относительно друг друга могут занимать два положения: точка лежит на прямой и точка не лежит на прямой.  Если точка С лежит на прямой АВ, то, на основании свойства проекций при параллельном проецировании, её проекции лежат на одноимённых проекциях этой прямой и на одной линии связи.  При рассмотрении свойств параллельного проецирования установлено, что отношение отрезков прямой равно отношению их проекций. Для того чтобы разделить отрезок прямой в заданном отношении, достаточно разделить в том же отношении проекции отрезка.  Пусть требуется отрезок АВ разделить точкой С в заданном отношении АС : СВ = 2:1. Обратимся к ортогональному чертежу отрезка АВ.

Нажмите на картинку для просмотра...

Например, из первой проекции В1 точки В проведём вспомогательную прямую под произвольным углом. На этой прямой отложим 3 равных отрезка любой длины. Соединим точку А1 и точку 3. Через точку 1 проведём прямую || А13. При пересечении этой прямой с отрезком А1В1 получим искомую точку С1, которая делит первую проекцию отрезка АВ в заданном отношении: А1С1 : С1В1 = 2:1. Так как по свойству проекций точки С1 и С2 должны лежать на одной линии связи, то теперь для того чтобы найти вторую проекцию С2точки С достаточно провести линию связи и найти точку её пересечения с отрезком А2В2. Отметим точку С2, которая удовлетворяет условию А2С2 : С2В2 = 2:1.

 Итак, мы построили на ортогональном чертеже отрезок АВ и отметили точку С, которая делит отрезокАВ в заданном отношении АС : СВ = 2:1.

Билет №7

Взаимное расположение двух прямых

Возможны три случая расположения прямых в пространстве:

1) прямые пресекаются, т. е. имеют общую точку;

2) прямые параллельны, т. е. не имеют общей точки, но лежат в одной плоскости;

3) прямые скрещиваются, т. е. не лежат в одной плоскости, т. е. через них нельзя провести плоскость.

Когда прямые пересекаются, на эпюре точки пересечения их одноименных проекций на горизонтальной и фронтальной плоскостях находятся на одном перпендикуляре к оси х.

Рассмотрим прямые I и II, которые пересекаются в точке А (рис. 26). Спроецируем обе прямые на горизонтальную плоскость. Если учесть, что точка А принадлежит обеим прямым, то ее проекция а будет принадлежать также и обеим проекциям прямых.

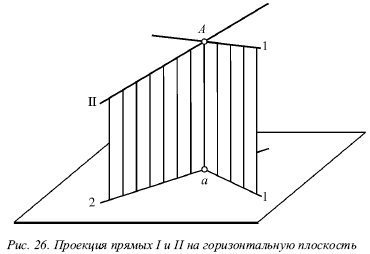
Похожая картина будет и на фронтальной плоскости, т. е. эти точки пересечения одноименных проекций а и а́ являются проекциями некоторой точки А, и поэтому они должны лежать на одном перпендикуляре к оси х. Точно так же будет верным и обратное утверждение: если на эпюре точки пересечения одноименных проекций прямых на две плоскости (горизонтальную и фронтальную) лежат на одном перпендикуляре к оси х, то эти прямые пересекаются.

Пусть проекции прямых I к II (рис. 27) подчиняются этому условию.

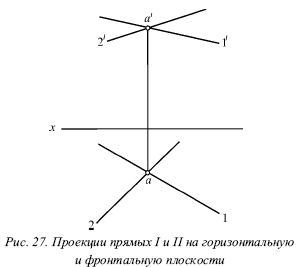
Тогда точки пересечения их одноименных проекций можно рассматривають как проекции некоторой точки в пространстве. Обозначим точку пересечения горизонтальных проекций 1 и 2 буквой а, а точку пересечения фронтальных проекций 1́ и 2́ – буквой а́. Рассматриваемая точка А находится и на прямой I, и на прямой II. То есть она является их общей точкой, в которой пересекаются эти прямые.

Прямое утверждение справедливо во всех случаях без исключения. Обратное же утверждение неприменимо в том случае, если хотя бы одна из прямых профильная.

Когда прямые параллельны, на эпюре их одноименные проекции параллельны (рис. 28).

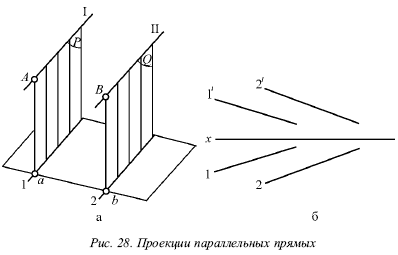
На самом деле, плоскости Р и Q, проецирующие прямые I и II на горизонтальную плоскость, параллельны, так как в каждой из этих плоскостей можно указать две пересекающиеся прямые, параллельные двум пересекающимся прямым второй плоскости, т. е. прямая I параллельна прямой II, и проектирующий луч Аа параллелен лучу Вb. Но две параллельные плоскости Р и Q пересекут горизонтальную плоскость. В результате этого образуются две параллельные прямые 1 и 2, т. е. горизонтальные проекции прямых I и II параллельны между собой.

Аналогично можно доказать, что и любые другие одноименные проекции обеих прямых также будут параллельны друг другу.

Верно и обратное утверждение: прямые параллельны, если на эпюре их одноименные проекции параллельны.

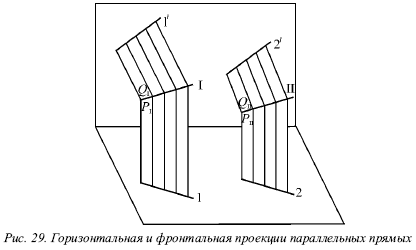
Если известно, что горизонтальные и фронтальные проекции прямых I и II параллельны, будет справедливо следующее: 1 || 2 и 1́|| 2́ (рис. 29).

В этом случае можно сказать, что плоскости Р_I и Р_II, проецирующие прямые I и II на горизонтальную плоскость, параллельны, так как в этих плоскостях можно указать по паре пересекающихся соответственно параллельных прямых (прямые 1 и 2 и проецирующие лучи). Аналогично плоскости Q_I и Q_II будут параллельны.

Прямая I находится в пересечении плоскостей Р_I и Q_I, а прямая II – в пересечении плоскостей Р_II Q_II. Отсюда получаем, что прямая I параллельна плоскости Р_II, потому что находится в плоскости, ей параллельной. Однако прямая I параллельна и плоскости Q_II. Поэтому прямая I параллельна линии пересечения плоскостей Р_II и Q_II, т. е. прямой II.

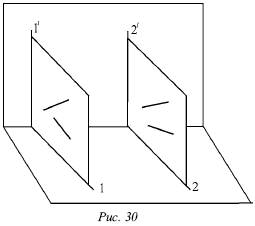
Доказательство обратного утверждения не имеет смысла для профильных прямых. Это объясняется тем, что тогда вместо двух плоскостей, проецирующих прямую на горизонтальную и фронтальную плоскости, существует только одна, дважды проецирующая плоскость (рис. 30).

Видно, что вне зависимости от расположения двух профильных прямых I и II в пространстве их горизонтальные и фронтальные проекции всегда параллельны (или сливаются).

Прямые будут являться скрещивающимися, если они не параллельны и не пересекаются. Это вытекает из того, что возможны только три случая взаимного расположения прямых.

Для скрещивающихся прямых справедливы утверждения:

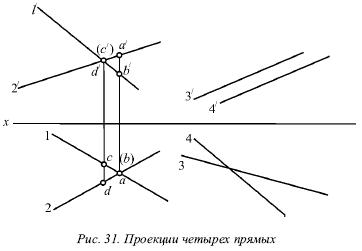
1) точки пересечения одноименных проекций на горизонтальной и фронтальной плоскостях не лежат на одном перпендикуляре к оси х (прямые I и II на рис. 31).

2) хотя бы в одной паре одноименные проекции не параллельны (прямые III и IV на рис. 31).

Рисунок 31 показывает проекции четырех прямых, любая пара из которых скрещивается.

Как и в рассмотренных ранее случаях, обратное утверждение для скрещивающихся прямых несправедливо при условии, что хотя бы одна из прямых является профильной.

Билет №8

Угол - геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Углом между прямыми называется меньший из двух углов между лучами, параллельными этим прямым. Углом между плоскостью и не перпендикулярной ей прямой называется угол между прямой и её проекцией на данную плоскость.

 

Рассмотрим ряд свойств ортогональных проекций плоских углов:

1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла)

Рисунок 3.25. Теорема о проецировании  прямого угла	Рисунок 3.26. Обратная теорема о проецировании прямого угла

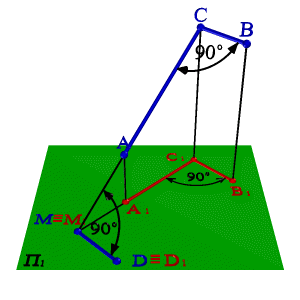
Дано: АВС 90^о; ВС// П₁; АС П₁.

Для доказательства теоремы продлим отрезок АС до пересечения с плоскостью П₁ получим горизонтальный след прямой -  точку М  М₁, одновременно принадлежащую прямой и ее проекции. Из свойства ортогонального проецирования следует, что ВС// В₁С₁. Если через точку М проведем прямую  МD параллельную С₁В₁ , то она будет параллельна и СВ, а следовательно  СМD90^о. Согласно теореме о трех перпендикулярах С₁МD90^о. Таким образом, MDА₁С₁ и MD//В₁С₁, следовательно, А₁С₁В₁ 90^о, что и требовалось доказать. В случае когда АСП₁ проекцией угла, согласно свойствам ортогонального проецирования, будет прямая линия.

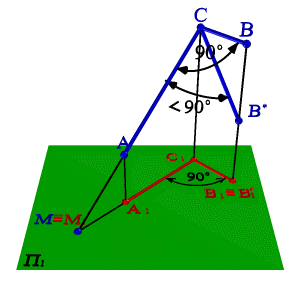
2. Если проекция угла представляет угол 90⁰, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций .

3. Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу. 

4. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.

5. Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением.

Любое сечение поверхности шара плоскостью является окружностью, которая проецируется без искажения только в том случае, если секущая плоскость параллельна плоскости проекций. В общем же случае мы будем получать эллипс. В том случае, если секущая плоскость перпендикулярна плоскости проекций, на этой плоскости проекцией окружности является отрезок прямой, который равен диаметру этой окружности

Билет №9

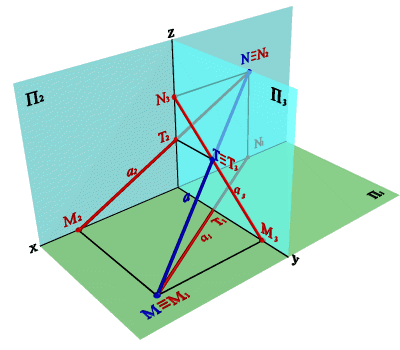
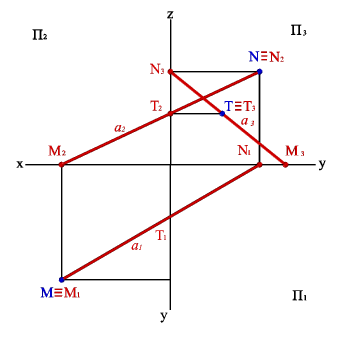
Следом прямой линии называется точка (рис. 26), в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её  координат должна быть равна нулю).

Горизонтальный след - М (z_M=0)-точка пересечения прямой с горизонтальной плоскостью проекций.

Фронтальный след - N (y_N=0)- точка пересечения прямой с фронтальной плоскостью проекций.

Профильный след - Т (x_Т=0)- точка пересечения прямой с профильной плоскостью проекций.

а) модель			б) эпюр
Рисунок 26.Следы прямой линии в системе трех плоскостей проекций

Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с  самим следом, а другие проекции лежат на осях. Например, фронтальный след прямой N₂N, а N₁ лежит на оси x, N₃ - на оси z. Отмеченные особенности в расположении следов  проекций позволяет сформулировать  следующие правила:

1. Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью 0x и в этой точке восстановить перпендикуляр  к оси до пересечения с горизонтальной проекцией прямой.