Лабораторные работы / Практическая работа №1

Цель работы: изучить методы исследования устойчивости стационарных и нестационарных линейных непрерывных и дискретно-непрерывных САР.

Задание:

Период дискретизации T₁=2.

Общая передаточная функция будет иметь вид:

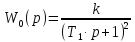
T=0,2

k=2

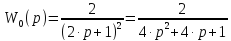
Исследуем систему по критериям устойчивости: Ляпунова, Гурвица, Раусса, Льенара-Шипара, Шур-Кона, Михайлов-Найквист, D-разбиение

Критерий Ляпунова.

1. Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то исходная система, описанная нелинейным дифференциальным уравнением устойчива. При этом никакие отброшенные при линеаризации члены второго и выше степеней отклонения не могут изменить устойчивость системы.

2. Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то исходная система неустойчива, при этом никакие отброшенные отклонения второго и выше степеней не могут придать системе устойчивость.

3. Если характеристическое уравнение системы имеет хотя бы один вещественный корень или пару чисто мнимых корней, то поведение действительной системы не может определяться ее линеаризованным уравнением, то есть линеаризованная система находится на границе устойчивости и отброшенные при линеаризации отклонения второй и высшей степеней коренным образом изменяют описание динамического процесса реальной системы.

Решим характеристическое уравнение системы:

,

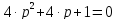Получим корни:

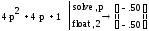
Построим значения корней на комплексной плоскости:

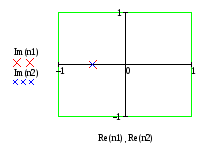
Рисунок 1 – Корни характеристического уравнения на комплексной

плоскости

Так как корни данного характеристического уравнения имеют отрицательное значение, то есть лежат в левой полуплоскости, следовательно, система устойчива.

Критерий Гурвица.

При составлении уравнения используют уравнение вида:

и составляется главный определитель Гурвица. Для этого все коэффициенты, начиная с (n-1) выписываются последовательно до свободного члена диагонали. Столбцы вверх от главной диагонали дополняются коэффициентами с возрастающими индексами. Места в которых должны стоять коэффициенты с индексами выше a_n и ниже a₀, заполняют нулями. В результате получают определитель из n – столбцов. Его первая строка состоит из нечетных коэффициентов, начиная с a₁, вторая строка включает все четные коэффициенты, третья строка и четвертая получаются соответственно из первой и второй сдвигом вправо на один элемент, на освободившееся место ставится нуль.

Чтобы характеристическое уравнение имело все корни с отрицательной вещественной частью, главный определитель и все его диагональные миноры должны иметь один знак с коэффициентом a₀ и быть больше нуля.

Система на границе устойчивости, если выполняется условие 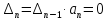. Это возможно, если a_n=0, тогда система находится на границе устойчивости и если минор A_n-1=0 система находится на границе колебательной устойчивости.

Характеристическое уравнение системы имеет вид:

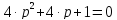
Составляем определитель Гурвица:

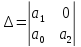
Определяем значения миноров:

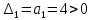
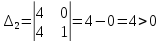
Так как все миноры определителя Гурвица положительны, то система

устойчива.

Критерий Раусса

Критерий Раусса является алгебраическим критерием и позволяет по коэффициентам характеристического уравнения определить место нахождения корней без решения характеристического уравнения.

Критерий Раусса оформляется в виде таблицы, при этом коэффициенты уравнения, имеющие четные индексы записываются в первую строку, нечетные -во вторую, остальные строки рассчитываются.

Если в полученной таблице все коэффициенты первого столбца больше нуля, то вещественные части всех корней характеристического уравнения отрицательны и система устойчива. Если хотя бы один коэффициент первого столбца меньше или равен нулю, то система неустойчива, при чем число переменных знаков этого столбца показывает число корней с положительной вещественной частью.

Чтобы система была устойчивой необходимо и достаточно, чтобы все величины первого столбца были больше нуля при положительном коэффициенте a₀, характеристического уравнения вида:

Для устойчивости системы необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Раусса были положительны.

Коэффициенты третьей сроки, вычисляются по формуле:

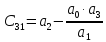
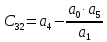
где

4. Коэффициенты четвертой сроки, вычисляются по формуле

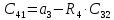
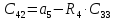
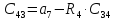
где

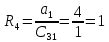
5. Коэффициенты n-ой сроки, вычисляются по формуле

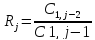
где i – номер столбца, j – номер строки.

Составим таблицу:

№ Строк	R	1 столбец	2 столбец
1		4	1
2		4	0
3	1	1	0
4	4	0	0

Все коэффициенты первого столбца положительны, следовательно, система устойчива.

Критерий Льенара-Шипара

Запишем условия устойчивости в форме Льенара-Шипара для характеристических уравнений до 6-го порядка включительно, пользуясь определителем Гурвица. Обозначим через 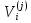миноры определителя Гурвица, стоящие на главных диагоналях, где индексы: i – порядок минора, а j – степень рассматриваемого характеристического уравнения. САР будет устойчива, если при a_i>0 нечетные миноры главной диагонали будут положительными. Для характеристических уравнений разных степеней вида условия устойчивости имеют следующий вид:

для 1-й степени

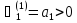
для 2-й степени

для 3-й степени

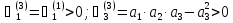
Для устойчивости системы необходимо и достаточно, чтобы все диагональные миноры определителя Гурвица с четными или нечетными индексами были больше нуля.

Характеристическое уравнение имеет вид:

+1=0

Это характеристическое уравнение второго порядка, тогда получаем:

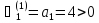
Следовательно, система устойчива, так как диагональные миноры определителя Гурвица больше нуля, то есть являются положительными.

Критерий Шур-Кона

Данный критерий позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому уравнению замкнутой системы, записанному в форме z – преобразований.

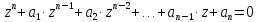
Полученная дискретная функция из исходной передаточной функции, имеет вид:

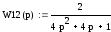
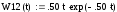
Запишем характеристическое уравнение:

z² -1.25z + 0.39 = 0

По уравнению запишем коэффициенты в виде определителя:

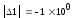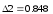<0

>0

Из полученных определителей следует, что дискретная система устойчива, так как полученные нечетные определители являются отрицательными, а четные - положительными.

Критерий устойчивости Михайлова

Критерий устойчивости Михайлова является геометрическим приложением принципа аргумента для анализа устойчивости замкнутой системы управления по виду годографа, который может быть получен из характеристического уравнения.

Имеем характеристическое уравнение вида:

Характеристическое уравнение разомкнутой системы имеет вид:

4p² + 4p + 1 =0

В данном выражении заменим р на jω, получим:

_{Выделим мнимую и реальную части, т.е. Re(Wл(ω)) и Im(Wл(ω)), построим АФЧХ разомкнутой системы:}

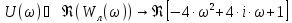
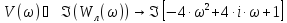
Для того, что бы система была устойчивой необходимо и достаточно, чтобы кривая Михайлова, начинаясь на положительной полуоси проходила последовательно n квадрантов в направлении против часовой стрелки, где n порядок характеристического уравнения. (n=2).

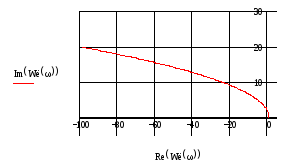
Рисунок 2 – График Михайлова

Система устойчива, так как годограф Михайлова, проходит два квадранта начиная с вещественной оси.

Критерий Найквиста.

Для устойчивости замкнутой системы при устойчивой разомкнутой системе необходимо и достаточно, чтобы годограф Найквиста, построенный по характеристическому уравнению разомкнутой системы, не охватывал точку (-1, j0).

Характеристическое уравнение разомкнутой системы имеет вид:

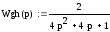
В данном выражении заменим р на jω, получим:

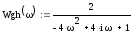
_{Выделим мнимую и реальную части, т.е. Re(Wgh(ω)) и Im(Wgh(ω)), построим АФЧХ разомкнутой системы:}

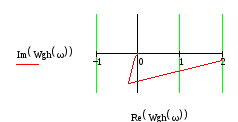
Рисунок 3 – График устойчивости по критерию Найквиста

Данная система устойчива, т.к. годограф Найквиста не охватывал точку (-1, j0), при изменении частоты w от 0 до +∞.

D-разбиение

Разбиение пространства коэффициентов на области, в которых число правых корней остается неизменным и выделение из них области D(0), называется D – разбиением.

Для упрощения поиска области устойчивости переходят к плоскости, для этого один из коэффициентов характеристического уравнения (например а₂) фиксируют, а₂ = const означает плоскость, которая пересекает некоторую поверхность по некоторой линии. Эта линия описывается только двумя координатами.

Имеем характеристическое выражение вида:

+1=0

Общий вид уравнения:

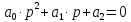
Для заданного характеристического уравнения построим область устойчивости по параметру а₁ = 1, выразим его:

а₁ = -4р² - 4р

Приравняем правую часть к нулю и произведем замену 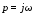, выделим действительную и мнимую части:

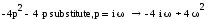
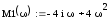
Выделяем мнимую и реальную часть, изменяем ω от - ∞ до ∞ и строим область устойчивости:

Рисунок 4 – График D разбиение

Строя границу D – разбиения в плоскости А, видим, что кривая пересекает вещественную ось в точке, для которой ω равна 0. Перемещаясь вдоль кривой от точки ω = - ∞ до ω = ∞, заштрихуем ее слева. Областью устойчивости является то, что находится слева от прямой, примыкающая к началу координат, чтобы убедится в этом приравняем точку А к нулю и определим корни полученного уравнения:

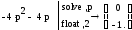
Получили, что один корень р₁ имеет нулевое значение, а другой р₂ действительное отрицательное, т.е. l=1. Т.к. в зоне I к+1= i+l, где i=1, следовательно, к+1=2. Т.к. порядок заданного характеристического уравнения второй, следовательно, данная зона соответствует устойчивой системе. При этом параметр А изменяется в диапазоне действительных чисел. Следовательно, система устойчива.

Вывод: проведя исследование системы по всем критериям устойчивости, и проанализировав полученные результаты можем сделать вывод, что система является абсолютно устойчивой.