Экономическая статистика
6.09.11
Быстров Олег Филаретович
Предмет, метод и задачи статистики
Статистика зародилась вместе с гос-вом. В Др. Китае учитывались имущественные состояния граждан. Численность населения, разрабатывались отчеты об уплате налогов и т.д. Статистика означает учет, порядок, состояние.
По мере развития статистики ее содержательная часть уточнялась, развивалась, сейчас есть около 200 определений статистики. Обилие определений свидетельствует о его сложности. Любая наука отличается от других объектом и предметом исследования. Под объектом исследования понимают некоторое явление, под предметом исследования – некую часть этого явления.
Объектом исследования статистики являются социально-экономические процессы и закономерности.
Предметом исследования статистики считается количественные закономерности в массовых случайных явлениях.
Всякая наука характеризуется своей специфической методологией. Методология представляет собой способ научного познания: совокупность принципов и методов исследования.
Основными методами исследования в статистике являются:
1)статистическое наблюдение,
2)сводка и группировка статистических данных
3)метод расчета обобщенных показателей
4)выборочный метод
Перечисленными методами в статистике решаются следующие задачи:
1)Выявление закономерностей в массовых случайных явлениях
2)Выявление зависимости между наблюдаемыми переменными и явлениями
3)Расчет статистических показателей
4)Выявление тенденций в статистических данных
и др.
У статистики есть свои категории (основные понятия):
1)статистический показатель
2)наблюдаемая переменная (или признак)
3)статистическая закономерность
4)генеральная совокупность
5)случайная выборка
и др.
В статистике существует понятие репрезентативности случайной выборки – представительность, точность, достоверность, соответствие реальным явлениям.
Выборочный метод статистики
Суть ВМ состоит в том, что наблюдая и исследуя только часть статистических данных, осуществляется суждение о всей совокупности данных, например все социологические опросы есть примеры выборочного метода.
Генеральная совокупность – множество всех значений наблюдаемой переменной.
Случайная выборка – это некоторая часть значений наблюдаемой переменной, выбранных случайным образом из генеральной совокупности.
Задача 1
Имеются данные об уставном капитале 30ти банков (в млрд.):
2,4 17,5 2,7 2,1 23,1 18,7 5,3 2,2 6,8 3,5
13,6 8, 9 2,2 9,0 3,6 7,5 4,3 5,1 9,9 2,9
13,4 4,8 5,0 6,1 5,9 17,2 20,5 10,7 2,9 12,1
Приведенные данные представляют собой статистический признак, т.е. некоторую отдельную характеристику изучаемого явления. Это количественный признак. Наряду с количественным признаком в статистике рассматриваются атрибутивные признаки, т.е. признаки, не имеющие числового выражения. Например, пол человека, цвет и т.д. Из приведенных данных видно, что такая наблюдаемая переменная, как уставный капитал банка, имеет множество различающихся значений. Если бы этих различий не было бы, то не было бы статистики. Изменчивость значений наблюдаемой переменной называют вариативностью. Для измерения вариативности в статистике есть свои показатели. Будем считать приведенные данные генеральной совокупностью, в которой учтены все банки некоторого региона. Эти данные можно упорядочить в виде вариационного ряда, т.е. расположить их от наименьшего значения до наибольшего. В данном случае вариационный ряд имеет вид:
2,1 2,2 2,2 2,4 2,7 2,9 2,9 3,5 3,6 4,3
4,8 5,0 5,1 5,3 5,9 6,1 6,8 7,5 8,9 9,0
9,9 10,7 12,1 13,4 13,6 17,2 17,5 18,7 20,5 23,1
Рассматриваемые статистические данные являются результатом статистического наблюдения, т.е. специальным образом организованного исследования. В данном случае статистическое наблюдения является сплошным. Различают также несплошное статистическое наблюдение, например случайную выборку из генеральной совокупности либо специальную выборку, например, когда исследуются банки после определенного уровня или значения уставного капитала. Статистические данные часто подвергают группировке, т.е. некой классификации. Простейшим видом группировки данных является отнесение их к ряду выделенных интервалов. Для выделения интервалов на множество числовых данных необходимо определить наибольшее и наименьшее значения, т.е. первый и последний элементы вариационного ряда. Для удобства последующих расчетов левое значение первого интервала и правое значение последнего часто округляют (т.е 2,1 = 2; 23,1 = 24). Число интервалов в статистике обычно принимают равным от 5 до 12.
Проведем группировку: каждое из чисел нужно отнести к какому либо интервалу. Если число равно границе интервала, то относим его влево.
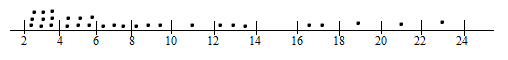
n1 = 9 n4 = 3 n7 = 0 n10 = 1
n2 = 6 n5 = 1 n8 = 2 n11 = 1
n3 = 3 n6 = 3 n9 = 1
Рассчитаем частоту попадания в интервал
Pi = ni/n
Р1= 9/30 Р4=3/30 Р7= 0 Р10=1/30
Р2= 6/30 Р5= 1/30 Р8= 2/30 Р11=1/30
Р3= 3/30 Р6= 3/30 Р9= 1/30
Т ь
∑ Pi = 1
Частота – это статистический показатель, который является статистической оценкой вероятности случайного события, в данном случае вероятности попадания значения наблюдаемой переменной в соответствующий интервал. Корректность использования такой статистической оценки обусловлено законом больших чисел, суть которого состоит в том, что
При неограниченном возрастании числа наблюдений, значение статистической оценки показателя сходится к истинному значению.
Закон больших чисел представляет собой некоторую совокупность теорем о сходимости различных статистических показателей к истинным значениям этих показателей.