
- •1 Техническое задание
- •1.1 Цель курсовой работы
- •1.2 Технические характеристики системы регулирования
- •1.3 Функциональная схема.
- •2 Выбор и обоснование выбора элементной базы
- •2.1 Выбор микропроцессора
- •2.2 Выбор захвата робота
- •2.3 Выбор гидропривода
- •2.4 Выбор редуктора
- •2.5 Выбор двигателя
- •2.6 Выбор датчика давления
- •2.7 Выбор датчика линейного перемещения
- •2.8 Выбор операционного усилителя
- •3 Деление лсу на изменяемую и неизменяемую части.
- •4 Построение характеристик и их анализ.
- •4.1 Построение ачх
- •4.2 Построение лачх и лфчх непрерывной системы
- •4.3 Построение переходной характеристики
- •4.4 Определение устойчивости дискретной системы
- •5 Построение желаемых лачх и лфчх. Анализ желаемой
- •5.1 Построение жлачх
- •5.2 Построение лачх корректирующего устройства
- •6 Синтез корректирующего устройства
- •6.1 Синтез параллельного корректирующего устройства
- •6.2 Синтез программного корректирующего устройства
- •6.3 Выбор корректирующего устройства
- •Уитс.424229.017.Пз
4 Построение характеристик и их анализ.
4.1 Построение ачх
Определение амплитуды входного сигнала и показатель колебательности системы автоматического в целом осуществляются по графику амплитудно-частотной характеристики дискретной системы автоматического регулирования.
Приведем исходную аналоговую систему к дискретной, введением микропроцессора. Частота опроса датчика составляет 1000 раз в секунду (период составляет T=0.001). Данная величина обусловлена необходимой точностью позиционирования захвата. Этого можно достичь лишь путем своевременного оповещения исполнительного органа о текущем состоянии системы.
Проведем z-преобразование, для чего воспользуемся функциями пакета Matlab. Реализация такого алгоритма требует введения экстраполятора нулевого порядка ‘zoh’ из функции c2d.
Получаем передаточную функцию разомкнутой системы:
 (49)
(49)
Перейдем к псевдочастоте, для чего введем замену:
![]() ,
(50)
,
(50)
с учетом, которой получаем:
 (51)
(51)
Перейдем
к псевдочастоте, используя замену
![]() ,
получаем
,
получаем
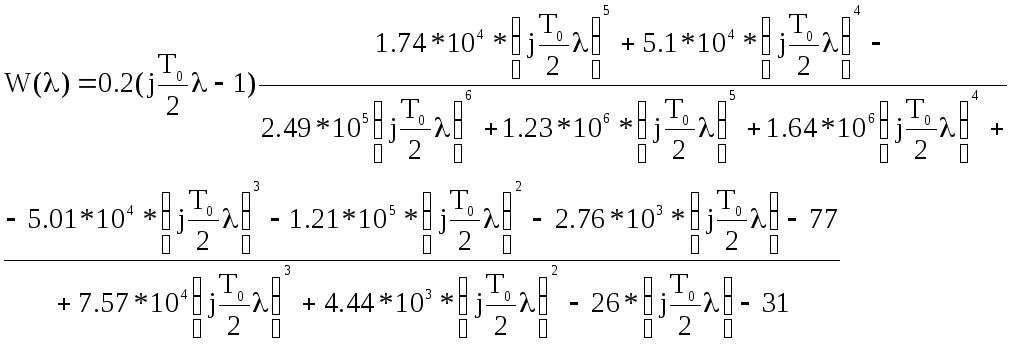 (52)
(52)
Амплитудная характеристика получается путем внесения реальной и мнимой части (52) в формулу:
![]() (53)
(53)
Исходя из (53), получен график АЧХ (рис. 8), кроме того, использовалась функция bode(Wz), где Wz – передаточная функция разомкнутой цифровой системы.

Рисунок 9 – АЧХ замкнутой системы
Из графика АЧХ, определяем необходимые показатели:
- максимальная амплитуда АMAX=17
-
показатель колебательности
![]()
4.2 Построение лачх и лфчх непрерывной системы
Для определения запасов устойчивости требуется построение логарифмических характеристик для разомкнутой системы, согласно (52). Для одновременного определения запасов устойчивости используем функцию margin(Wz) пакета MatLab.
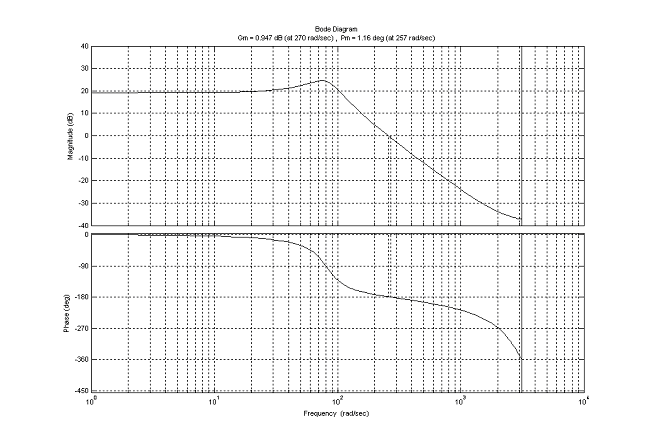
Рисунок 10
Из графика 7 определены запасы устойчивости:
-
запас по амплитуде 0.947 дБ
-
запас по фазе 1.160
4.3 Построение переходной характеристики
Построим переходную характеристику для замкнутой системы, согласно (48), для чего воспользуемся функцией step(Wzz) пакета MatLab.
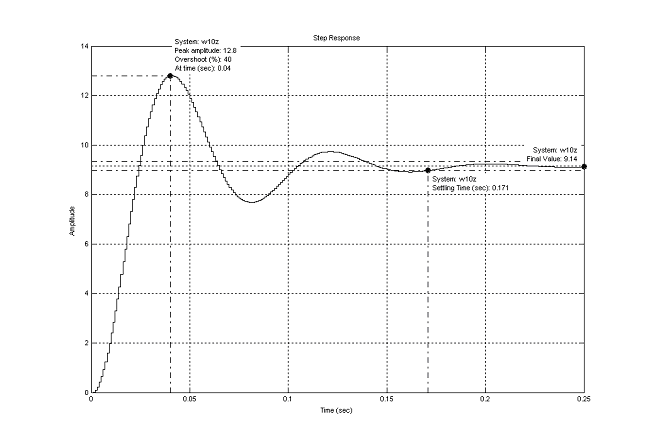
Рисунок 11
Из графика можно определить следующие характеристики:
1. Время регулирования tp=0.158 c
2. Перерегулирование σ=(10.9-7.61)/10.9=30 %
Из графика переходного процесса видно, что быстродействие системы более чем достаточное, однако присутствует большое перерегулирование, что в моей системе не допустимо. Таким образом, требуется установка корректирующего устройства.
4.4 Определение устойчивости дискретной системы
Для определения устойчивости воспользуемся критерием Шур-Кона, согласно которому, дискретная система будет устойчива, если все корни характеристического уравнения будут находиться внутри единичной окружности.
Для (48) перейдем к дискретной форме записи. Проведем z-преобразование, для чего воспользуемся функциями пакета Matlab. Реализация такого алгоритма требует введения экстраполятора нулевого порядка ‘zoh’ из функции c2d.
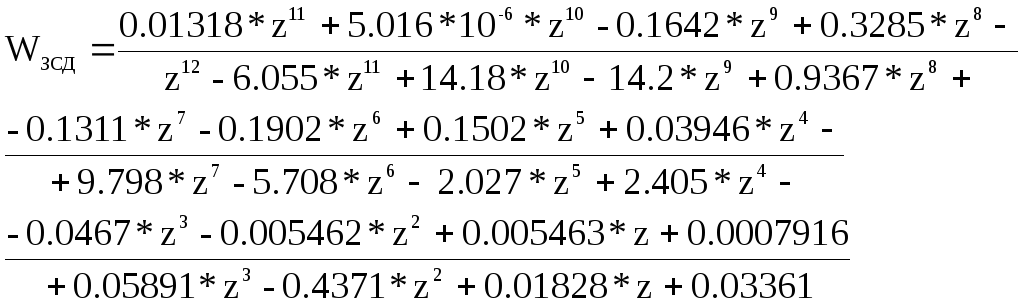 (54)
(54)
Для большей точности, продолжим вычисления в пакете MatLab, для чего используем функцию нахождения нулей и полюсов zpk(w). Выпишем сразу характеристическое уравнение в виде:
![]() (55)
(55)
Корни характеристического уравнения, можно найти, используя функцию solve(W) пакета MathCad.
Для первых некоторых членов (55) они одинаковы: z1=-0.9987, z2=0.9987, z3=-0.9961, z4=0.9961, z5=-0.8207, z6=0.8207, z7=-0.8207, z8=0.8207.
Согласно критерию Шур-Кона дискретная система устойчива, т.к. все корни характеристического уравнения лежат в единичном круге.
