
3 Деление лсу на изменяемую и неизменяемую части.
ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ
К неизменяемой части относят все элементы регулятора с передаточной функцией отличной от единицы. Следовательно, к ним можно отнести все элементы кроме микропроцессора.
Определим передаточную функцию системы, передаточная функция главной цепи будет:
![]() .
(29)
.
(29)
![]()
Передаточная функция разомкнутой системы будет:
![]() .
(30)
.
(30)
![]()
Передаточная функция замкнутой системы:
![]() .
(31)
.
(31)
По выражению (30) построим АФЧХ разомкнутой системы, изображенную на рисунке 3:
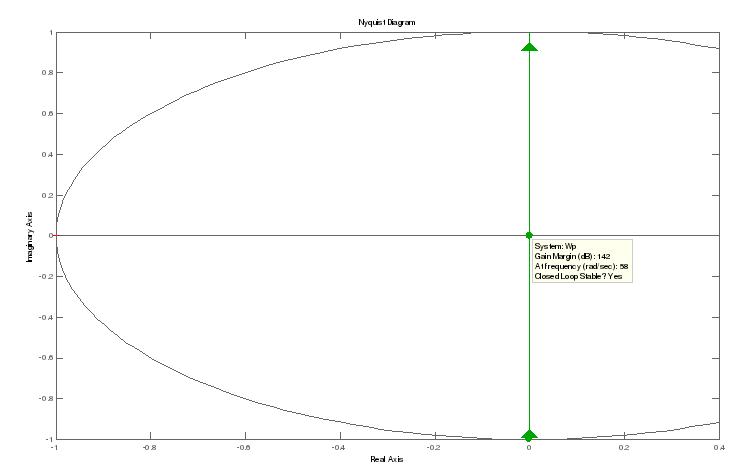
Рисунок 4 – АФЧХ разомкнутой системы
Согласно критерию Найквиста, замкнутая автоматическая система регулирования будет устойчивой, если АФХ разомкнутой системы не охватывает точку с координатами -1,j0 ,таким образом, имеем устойчивую систему с неограниченно большими запасами по амплитуде и фазе [6].
Переходный процесс в замкнутой системе изображен на рисунке 5. Из него видно что переходный процесс длится более 16 секунд лишь потом становится устойчивым. Такой отпечаток накладывает инерционное звено.
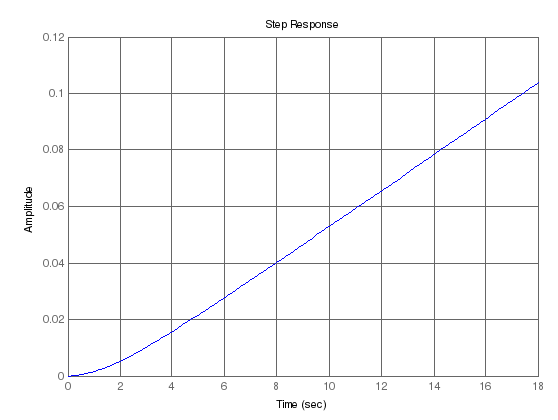
Рисунок 5 – переходный процесс разомкнутой системы
 АЧХ
системы выглядит следующим образом:
АЧХ
системы выглядит следующим образом:
Рисунок 6 – переходный процесс разомкнутой системы
Запасы устойчивости определим по АЧХ системы:
запас по амплитуде 119 дБ
запас по фазе 93,7 градусов
4 ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК И ИХ
АНАЛИЗ
4.1 Построение ЛАЧX
Разомкнутая система образована, соединенными последовательно, апериодическим, пропорциональным и колебательным звеньями:
![]() (32)
(32)
ω1=1/T1= 0,5882рад/c,
ω1=1/T1=3.02*103 рад/c.
 По
выражению (30) построим ЛАЧХ и ЛФЧХ –
рисунок 6, разомкнутой системы:
По
выражению (30) построим ЛАЧХ и ЛФЧХ –
рисунок 6, разомкнутой системы:
Рисунок 7 – ЛАЧХ и ЛФЧХ разомкнутой системы
4.2 Построение ЖЛАЧХ
Проведем построение ЖЛАЧХ методом запретной зоны
Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. ЖЛАЧХ состоит из трех основных асимптот: низкочастотной, среднечастотной и высокочастотной. Среднечастотная асимптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяют динамические свойства системы – устойчивость и показатели качества переходной характеристики.
Перейдем к дискретной системе с периодом дискретизации T=0.0005 c
![]() (33)
(33)
Л АЧХ
дискретной модели строится в зависимости
от псевдочастоты λ, при этом сначала
п
АЧХ
дискретной модели строится в зависимости
от псевдочастоты λ, при этом сначала
п![]() роводится
ω-преобразование заменяя z=(1+ω)/(1-ω), а
затем осуществляется
переход от W(ω) к частотному выражению
передаточной функции через псевдочастоту
λ путем замены ω=0.5Tλj.
роводится
ω-преобразование заменяя z=(1+ω)/(1-ω), а
затем осуществляется
переход от W(ω) к частотному выражению
передаточной функции через псевдочастоту
λ путем замены ω=0.5Tλj.
Рисунок 8 – ЖЛАЧХ,
построенная методом запретной зоны
Замкнутая система в дискретном виде:
![]()
![]() (34)
(34)
Зададим скорость g’= 27 и ускорение обработки g’’=120 информации, а также показатель колебательности M=1.2, max ошибка регулирования =0,2 (Amax=0.65)
Определяем рабочую точку:
=g’’/g’=120/27=4.44 рад/с - псевдочастота
A= Amax/=0.65/0.2=3.25
![]() Дб
Дб
тогда координаты рабочей точки (4.44 рад/с, 10.2 дБ)
Амплитуда на сопрягающих частотах
L1=![]() (35)
(35)
L2=![]() (36)
(36)
Вид запретной зоны показан на рис. 9:

Рисунок 9 –Вид запретной зоны
И сходную
ЛАЧХ и ЖЛАЧХ разомкнутой системы,
построенную методом запретной зоны
изобразим на рисунке 10.
сходную
ЛАЧХ и ЖЛАЧХ разомкнутой системы,
построенную методом запретной зоны
изобразим на рисунке 10.
Рисунок 10 – ЖЛАЧХ,
построенная методом запретной зоны
Передаточная функция замкнутой системы, скорректированной методом запретной зоны, будет иметь вид:
![]() . (37)
. (37)
Тогда переходный процесс в замкнутой системе скорректированной методом запретной зоны изобразим на рисунке 11:
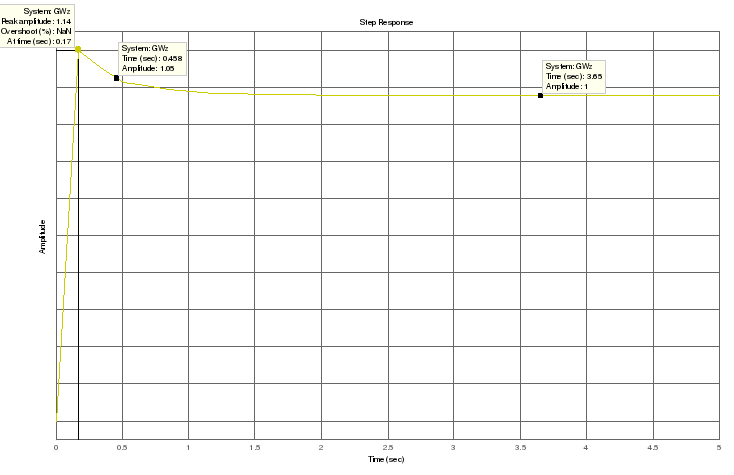
Рисунок 11 – Переходный процесс в замкнутой системе, скорректированной методом запретной зоны
Прямые оценки качества переходной характеристики:
1. Время регулирования tp=1,34 c;
2. Перерегулирование σ=0 %.
Данные показатели качества удовлетворяют заданным требованиям. Несоответствие показателей качества с их расчетными значениями объясняются значительным отличием вида вещественной частотной характеристики скорректированной системы от типовой.
5 СИНТЕЗ КОРРЕКТИРУЮЩЕГО ЗВЕНА
5.1 Синтез непрерывных корректирующих звеньев
Существует несколько способов включения корректирующего звена. Определим желаемую передаточную функцию для каждого из включений и выберем лучшую
Определим желаемую передаточную функцию последовательного корректирующего устройства:
![]() (38)
(38)
Упрощенное выражение:
![]() (39)
(39)
Определим желаемую передаточную функцию встречно – параллельного непрерывного корректирующего устройства:
![]() (39)
(39)
Определим желаемую передаточную функцию параллельного непрерывного корректирующего устройства:
![]() (40)
(40)
Так как реализация корректирующего устройства должна быть по возможности более простой, то анализируя формулы (38), (39), (40).
Построим ЛАХЧ последовательного корректирующего устройства

Рисунок 12 – ЛАЧХ последовательного корректирующего устройства
Полученное корректирующее устройство может быть реализовано в виде усилителя с неким коэффициентом усиления.
C1 .
.
Рисунок 13 – Схема последовательного корректирующего устройства
Передаточная функция дифференцирующего четырехполюсника:
 , (41)
, (41)
Передаточная функция первого дифференцирующего четырехполюсника:
 , (42)
, (42)
где KK1=R2/(R1+R2)=0,4255;
T1=R1*C1= 0,0392;
T2=KK1*T1=0,0921.
При этом усилитель должен иметь коэффициент усиления:
Ку=1249/0.0921= 13565 (43)
