
- •Введение
- •1 Расширенное техническое задание
- •Назначение лсау в данной курсовой работе в качестве проектируемой лсау рассмотрим систему автоматического управления душевой кабинкой на космической станции.
- •1.2 Состав лсау
- •1.3 Технические требования к проектируемой лсау
- •2 Выбор и обоснование выбора элементной базы лсау
- •2.1 Выбор микроконтроллера
- •2.2 Выбор клапана
- •2.10 Выбор смесителя
- •Выбор датчика
- •4 Расчет устойчивости системы
- •5 Построение лачх и лфчх непрерывной системы
- •6 Построение желаемой лачх и лачх корректирующего устройства.
- •6.1 Построение жлачх
- •7 Синтез корректирующего устройства
- •7.1 Синтез параллельного корректирующего устройства
- •7.2 Синтез программного корректирующего устройства
- •7.3 Выбор корректирующего устройства
- •Заключение
- •Список используемой литературы
2.10 Выбор смесителя
Параметры смесителя:
- максимальное давление, МПа 1,6;
- максимальный угол поворота, ° 90;
- максимальная температура, ° С 80;
- стандартное рабочее давления, мПа 0.4.
Элемент имеет нелинейную характеристику, представленную на рисунке 3
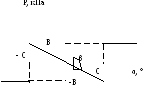
В – стандартное рабочее давление; С – максимальный угол поворота
Рисунок 3 - Статическая характеристика смесителя
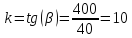 (36)
(36)
Отсюда передаточная функция
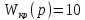 (37)
(37)
Выбор датчика
В качестве датчика используется электрический манометр серии ЭДМУ, в котором чувствительным элементом является мембранная коробка. Для преобразования деформации упругих элементов в электрический сигнал применяется омический (потенциометрический) преобразователь. В качестве указателей в манометрах обычно применятся логометры с подвижным магнитом.
Передаточная функция Wд(р) имеет вид:
Wд(р)= FЭФ, (38)
где FЭФ – эффективная площадь чувствительного элемента
R=0.04 м – радиус мембраны
FЭФ=2R =0.2512 м2 (39)
Отсюда передаточная функция
Wд(р)= 0.2512 (40)
3 РАСЧЕТ ДАТЧИКА ОБРАТНОЙ СВЯЗИ
Принцип действия мембранных манометров основан на измерении деформации гофрированной мембраны.
Связь между прогибом центра мембраны х и давлением р определяется соотношением:
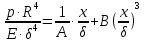 (41)
(41)
где A=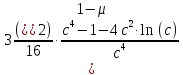 (42)
(42)
B=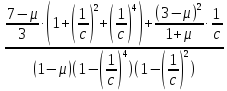 (43)
(43)
c=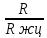 (44)
(44)
R - радиус мембраны, R=4 см;
Rж.ц - радиус жесткого центра, R=2 см;
р - давление в кГ/см2;
Е - модуль упругости материала, E=50 кГ/см2;
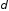 -
толщина мембраны,
-
толщина мембраны,
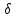 =1мм;
=1мм;
х - перемещение центра мембраны, x=0.5;
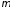 —коэффициёнт
Пуассона,
—коэффициёнт
Пуассона,
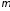 =0.25.
=0.25.
Отсюда с=2, А=0.043, В=11.336, р=0.03кГ/см2=2.94кПа
Допускаемый прогиб толстой мембраны определяется выражением:
хдоп=0.256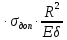 (45)
(45)
где  - допускаемое напряжение на растяжение
для материала мембраны
- допускаемое напряжение на растяжение
для материала мембраны
хдоп=2 см.
Удачное решение датчика давления получается при использовании мембраны с наклеенными омическими тензодатчиками. Механические напряжения на поверхности мембраны, заделанной по контуру, меняются вдоль радиуса r по законам меняются:
- для радиальных напряжений
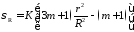 (46)
(46)
где 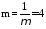 (47)
(47)
К=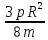 =45 (48)
=45 (48)
σR=78.75
- для тангенциальных напряжений
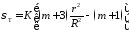 (49)
(49)
σT=56.25
Для повышения чувствительности иногда используют в одном датчике несколько мембран с наклеенными тензопреобразователями .
Для повышения быстродействия тонких плоских мембран, их иногда натягивают по контуру. Частота колебаний для этого случая определится по формуле:
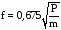 (50)
(50)
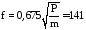 (51)
(51)
где Р - натяжение мембраны по периферии 7 кГ/см;
m – масса мембраны в 0,0025 кГ·сек2/см.
4 Расчет устойчивости системы
Элементная база САУ состоит из следующих компонентов:
душевая кабинка (ДК), вентилятор (В), электроподогреватель воздуха (ЭВ), сепаратор (С), резервуар с водой (Р), смеситель (Кр), насос (Н), загрязненной воды (Ф), микроконтроллер (МК), клапан электрический (КЭ), датчик (Д).
МК относится к изменяемой части, т.к. замена этого устройства не внесет серьезных изменений в характеристики системы.
Остальные же элементы относятся к неизменяемой части, т.к. эти устройство является специализированными для выполнения конкретных задач и имеют определенные технические характеристики, изменение которых может привести к серьезным изменениям характеристик всей системы.
Найдем передаточную функцию системы с помощью программы MathCad.
Проведя ряд преобразований и подстановок получим передаточную функцию замкнутой системы:
 (52)
(52)
Нули характеристического уравнения имеют вид -0.28; -3.1; -49; -1.7; -7.8; -5.4-1.1i; -5.4+1.1i.
Известно, что при отрицательных вещественных частях характеристического уравнения система устойчива, следовательно, система WЗС устойчива.
Построим переходный процесс САУ (рисунок 4). Для этого проведем обратное преобразование Лапласа от замкнутой передаточной функции САУ.
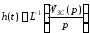 (53)
(53)

Рисунок 4 – Переходный процесс системы
По полученному переходному процессу определим показатели качества САР:
Установившееся значение hуст=0.036922
Тогда 5% интервал отклонения от установившегося значения будет соответствовать следующей величине.
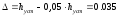
Перерегулирование
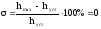 (54)
(54)
3) Время переходного процесса tп=13 с.
Время первого согласования (время, когда регулируемая величина в первый раз достигает своего установившегося значения) t1=22 c.
Период колебаний Т=∞.
Частота колебаний
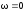 .
.Колебательность (число колебаний за время колебательного процесса) n=0.
Декремент затухания
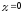 .
.
Определим косвенные оценки качества. Для этого построим амплитудно-частотную характеристику (рисунок 5).
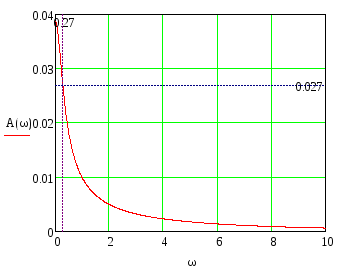
Рисунок 5 – Амплитудно-частотная характеристика САУ
1) Резонансная частота (частота при которой АЧХ достигает своего максимального значения) ωР=0.
2)
Показатель колебательности
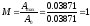
Передаточная функция разомкнутой системы:
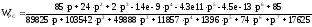
Корни характеристического уравнения

имеют вид -0.27, -1.6, -51, -3.1-1.4i, -3.1+1.4i, -7.6+3.2i, -7.6-3.2i.
Известно, что при отрицательных вещественных частях характеристического уравнения система устойчива, следовательно, система WРС устойчива.
Годограф Найквиста для разомкнутой системы представлен на рисунке 6.
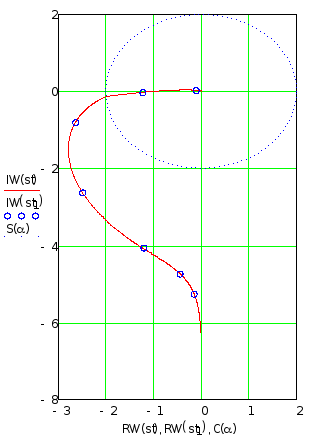
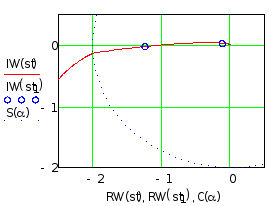
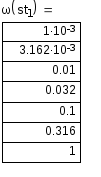
Рисунок 6 – Годограф Найквиста
Приведем исходную аналоговую систему к дискретной, введением микропроцессора. Частота опроса датчика составляет 10 раз в секунду (период составляет T=0.1). Данная величина обусловлена необходимой точностью измерения давления. Этого можно достичь лишь путем своевременного оповещения исполнительного органа о текущем состоянии системы.
Проведем z-преобразование разомкнутой системы, для чего воспользуемся функциями пакета MathCad.
В результате вычислений получим:
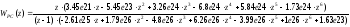 Аналогично
проведем z-преобразование
замкнутой системы
Аналогично
проведем z-преобразование
замкнутой системы
Передаточная функция замкнутой системы примет вид:
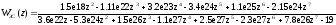
Определим устойчивость полученной импульсной системы по Критерию Шур - Кона. Для устойчивости импульсной системы необходимо, чтобы коэффициенты характеристического уравнения были положительны.
В нашем случае характеристическое уравнение имеет вид:
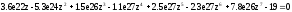
В характеристическом уравнении не все коэффициенты положительны, следовательно, импульсная система неустойчива.
Построение переходной функции импульсной системы. Используя программу Matlab и уравнение передаточной функции замкнутой системы в z – преобразованиях и проведя обратное z – преобразование этой функции, получим переходный процесс импульсной системы:
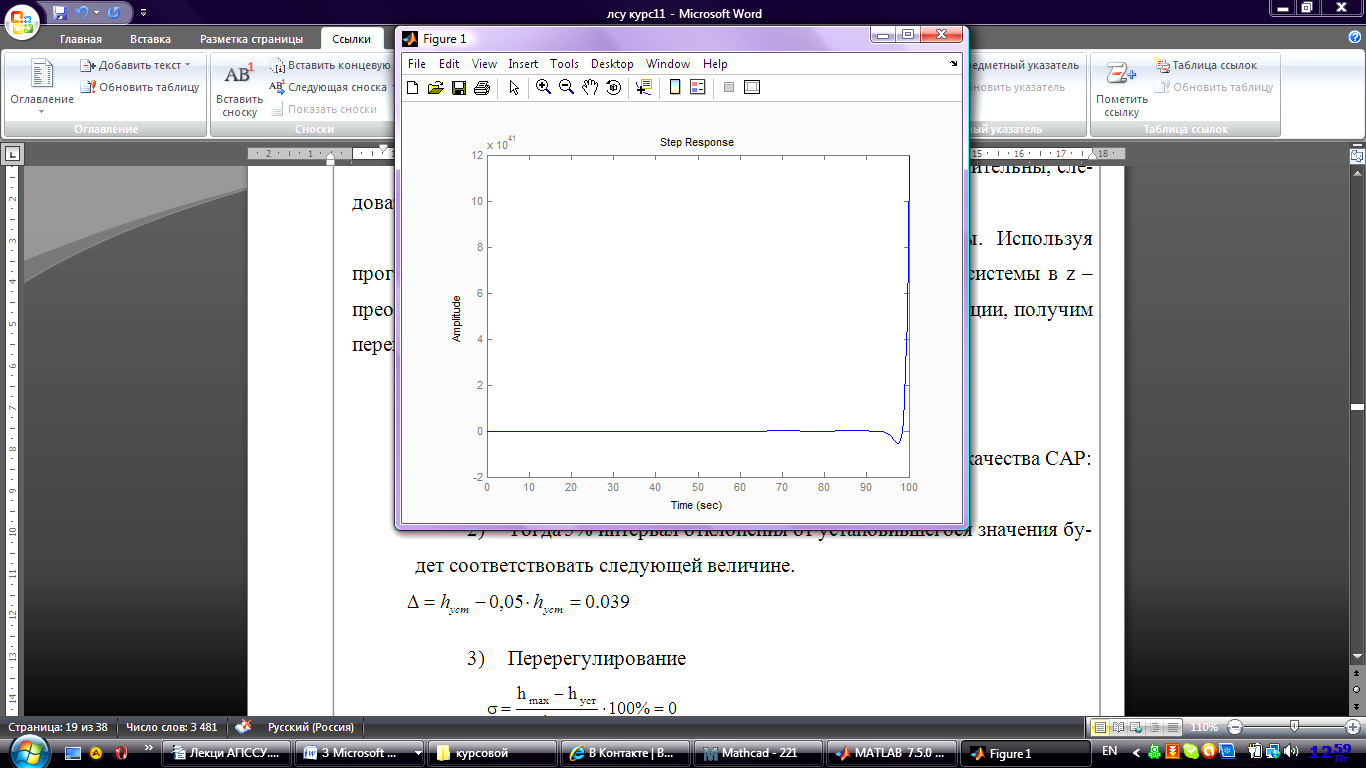
Рисунок 7 – Переходный процесс импульсной системы
По полученному переходному процессу нельзя показатели качества САР, поскольку он неустойчивый.
