§ 8. Линейное уравнение регрессии в стандартных масштабах
В этом параграфе мы рассмотрим связь коэффициента корреляции с линейным уравнением регрессии; при этом мы познакомимся с еще одной формой описания взаимосвязи — с уравнением в стандартных масштабах.
Рассмотренное в § 6 линейное уравнение регрессии устанавливало связь между результативным признаком y и признаком-фактором x, выраженными в естественных единицах измерения. При этом оказывались существенными и единицы измерения, и средние значения признаков, и показатели их вариации. Для того чтобы отвлечься от характеристик распределений каждого из признаков в отдельности и выделить лишь характеристики взаимосвязи признаков, при анализе вместо значений признаков в естественных единицах измерения широко используются так называемые нормированные отклонения (стандартизованные переменные). При этом индивидуальные значения признаков заменяются отклонениями от среднего арифметического значения, отнесенными к среднему квадратическому отклонению:
Нормированные отклонения любых признаков обладают следующими свойствами:
1) так как
(как среднее значение отклонения от
среднего арифметического), то и
;
2) вычислим дисперсию нормированного отклонения:
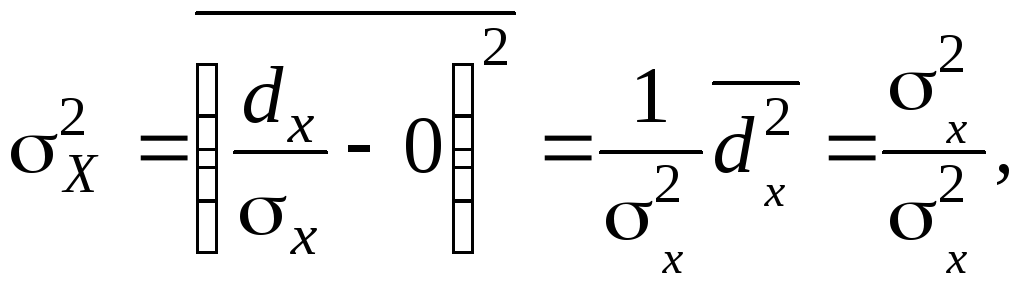
т.е.
;
3) пусть нам даны нормированные отклонения двух признаков X и Y. Найдем среднее значение их произведения:
Таким образом, нормированные отклонения двух признаков — это безразмерные величины, в среднем равные нулю, а среднее квадратическое отклонение каждой из них равно единице. Заменив фактические значения различных величин нормированными отклонениями, мы тем самым как бы стандартизовали их вариацию.
Уравнение регрессии, связывающее нормированные отклонения признаков, носит название уравнения регрессии в стандартных масштабах.
Нормированные отклонения отличаются от исходных переменных лишь началом отсчета и масштабом. Если связь между признаками линейна, то и нормированные отклонения связаны линейным уравнением. Регрессия в стандартных масштабах имеет следующий вид:
Для определения параметров и воспользуемся системой нормальных уравнений в форме средних (6.3). Для нормированных отклонений эта система имеет следующий вид:
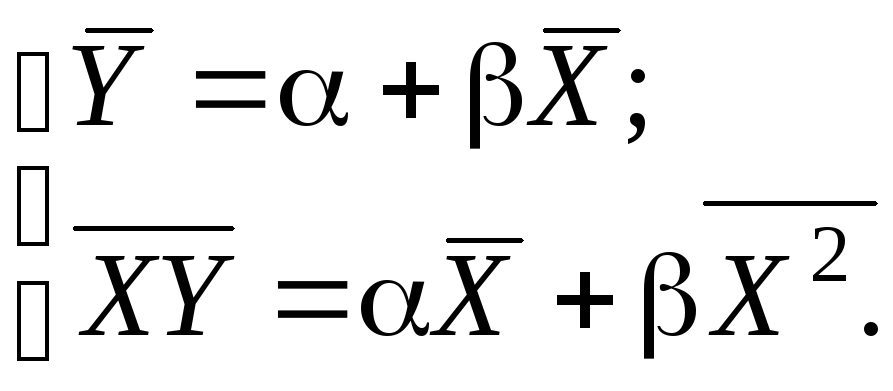
Так как
,
из первого уравнения следует, что
свободный член
равен нулю. Воспользуемся остальными
свойствами нормированных отклонений:
Таким образом,
.
Итак, линейное уравнение регрессии в стандартных масштабах имеет следующий вид:
(8.1)
Мы установили, что
коэффициент корреляции совпадает с
коэффициентом регрессии нормированного
отклонения Y
по нормированному отклонению
.
Следовательно, он отражает интенсивность
связи между нормированными отклонениями
и показывает, на какую долю своего
среднего квадратического отклонения
изменяется результативный признак при
изменении фактора на величину
.
Если нужно перейти от уравнения в стандартных масштабах к уравнению в естественных масштабах, следует подставить в уравнение (8.1) вместо нормированных отклонений их выражения через средние значения и средние квадратические отклонения:
Преобразуем это выражение:
Полученный результат совпадает с линейным уравнением регрессии в естественных масштабах
а параметры этого уравнения определяются следующими выражениями:
(8.2)
(8.3)
Отсюда следует порядок расчетов параметров уравнения регрессии:
1) определяются
средние значения и средние квадратические
отклонения признаков:
;
2) определяется
коэффициент корреляции
;
3) определяются параметры регрессии b и a по формулам (8.2) и (8.3).
Обратимся к примеру. Требуется найти регрессию времени обработки деталей по величине обрабатываемой поверхности по данным таблицы 6.1. Эту задачу мы уже решали с помощью системы нормальных уравнений. Теперь решим ее еще раз, но уже с помощью метода, изложенного в настоящем параграфе. Все промежуточные результаты получены в § 7 при определении коэффициента корреляции:
Определим параметры уравнения связи:
что полностью совпадает с полученным ранее результатом.
Роль коэффициента корреляции не ограничивается тем, что он является коэффициентом регрессии в уравнении в стандартных масштабах. Другую сторону этого коэффициента мы можем выявить, определяя корреляционное отношение для уравнения в стандартных масштабах.
Найдем остаточную дисперсию нормированного отклонения Y:
Но
.
Следовательно,
Отсюда находим корреляционное отношение:
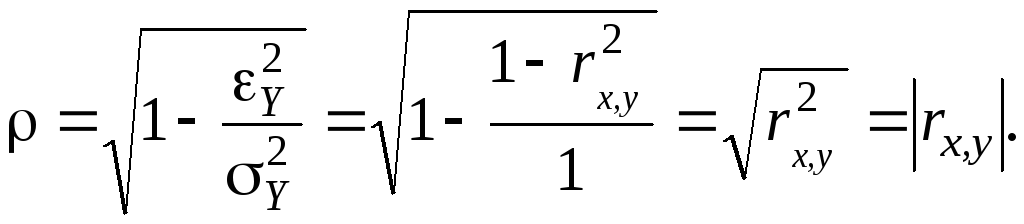
Так как величины
и y
отличаются лишь масштабами, ясно, что
структура дисперсии величины y
повторяет структуру дисперсии
нормированного отклонения Y;
все составляющие дисперсии y
в
раз больше соответствующих составляющих
.
Следовательно, и корреляционное отношение
для линейного уравнения регрессии в
естественных масштабах также равно
т. е. абсолютная величина коэффициента корреляции совпадает с корреляционным отношением для линейного уравнения регрессии.
Остаточная вариация величины y в естественных масштабах определяется равенством:
В нашем примере
Таким образом, при использовании методов, описанных в настоящем параграфе, попутно с определением параметров уравнения регрессии определяется также показатель тесноты связи.
Отмеченные свойства коэффициента корреляции позволяют охарактеризовать его как показатель тесноты линейной связи; в литературе его иногда называют линейным коэффициентом корреляции.