Приложения Приложение I. Теорема о разложении дисперсии

Известно следующее свойство, которым обладает вариация признака y в произвольной совокупности:

Здесь — среднее значение признака в данной совокупности, A — любое число. Если применить это свойство к некоторой группе, роль среднего арифметического будет играть групповое среднее :

где — дисперсия признака y в i-й группе:

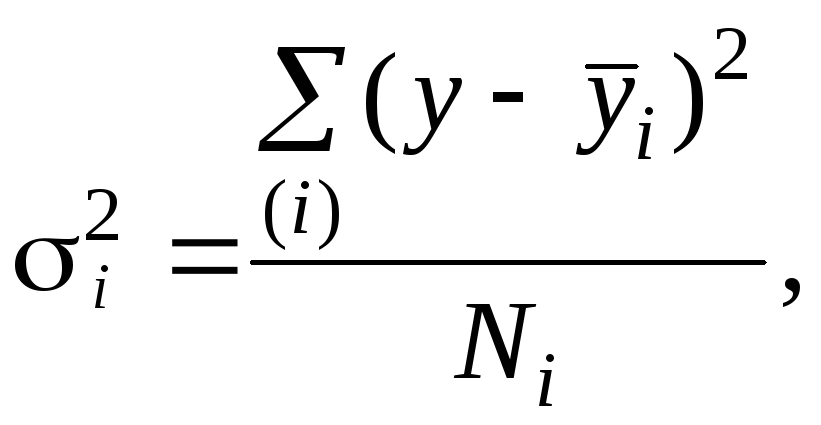
где символ означает суммирование по элементам i-й группы. В частности, в качестве числа A может быть взято среднее значение по всей совокупности , которое для данной группы особыми свойствами не обладает. Если раскрыть усреднение в левой части, отмеченное свойство примет вид:

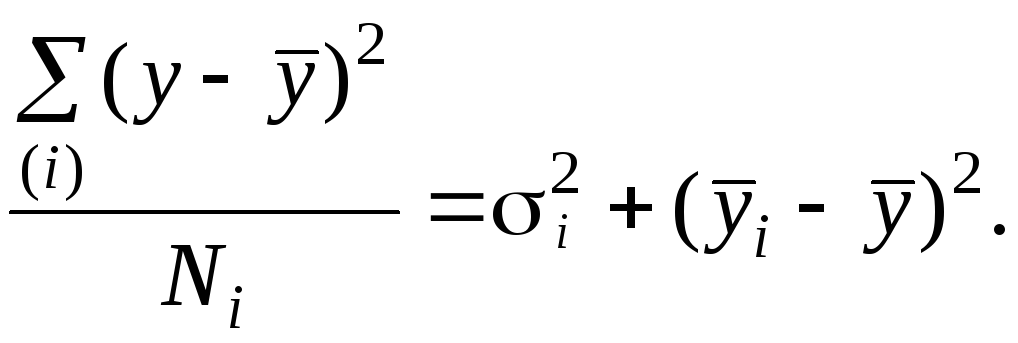
Умножим обе части полученного равенства на численность i-й группы :

Такие равенства должны выполняться во всех группах, на которые разбита совокупность: Почленно сложим эти равенства по всем группам:

В левой части равенства все суммы по элементам отдельных групп объединились в одну сумму по элементам всей совокупности. Разделив последнее равенство на объем совокупности , получим:

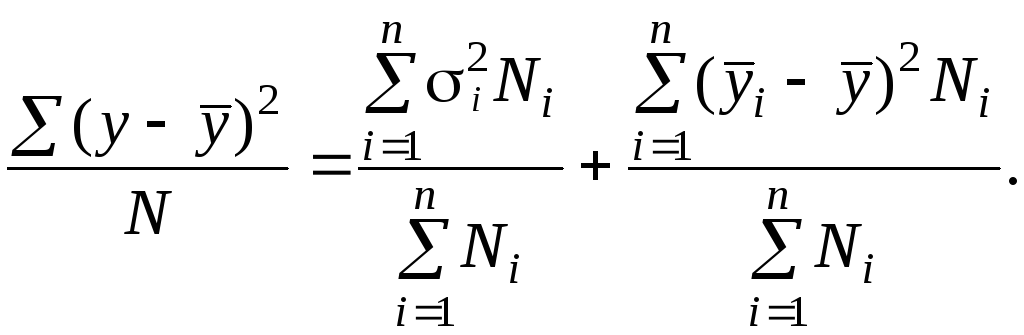
В левой части у нас получилась дисперсия признака во всей совокупности; правая часть состоит из двух слагаемых. Первое из них — это среднее значение из дисперсий отдельных групп, взвешенное по численностям этих групп (внутригрупповая дисперсия):

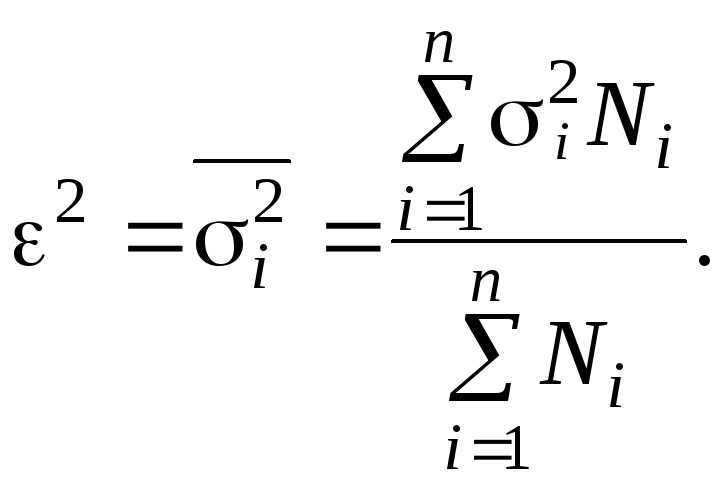
Второе слагаемое представляет собой средний квадрат отклонений групповых средних от общей средней, также взвешенный по численностям групп:

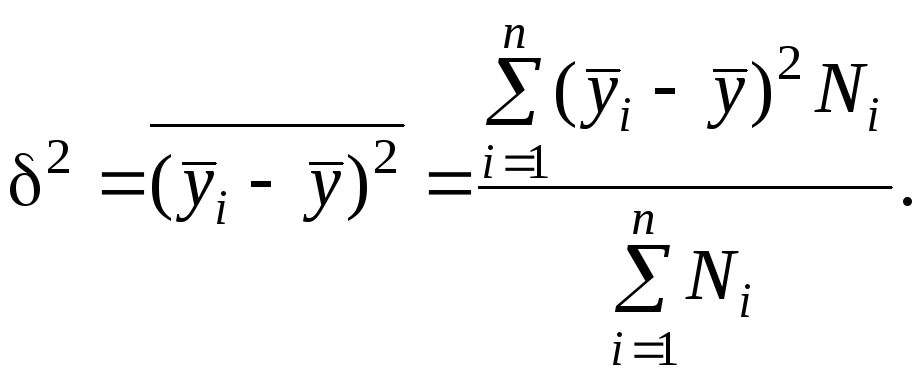
Эта величина получила название межгрупповой дисперсии.

Итак, мы доказали теорему о разложении дисперсии:

.

Приложение II. Теорема о среднем значении регрессии

В этом и следующем приложениях рассматриваются полезные свойства регрессии, порождаемые свойствами тех классов функций, в которых ищется регрессия. Будут доказаны достаточно общие утверждения, относящиеся и к однофакторным, и к многофакторным регрессиям. Речь пойдет о функциях , число и характер аргументов которых не будут иметь значения, и о классах таких функций, определенные свойства которых будут представлять интерес. Будем использовать обозначение x для набора факторов — аргументов функции . Результирующую переменную y будем считать вещественной.

Рассмотрим класс функций , обладающий тем свойством, что любая функция из этого класса при прибавлении к ней любой константы остается в этом же классе, т. е. из   следует a , где a — произвольная константа. Пусть ₀ — МНК-регрессия переменной y в классе . Покажем, что в этом случае  .

Введем в рассмотрение величину z  ₀(x) и рассмотрим регрессию ₁(z; a)  a  z, имеющую один параметр — «свободный член» a. Система нормальных уравнений для определения этого параметра состоит из единственного уравнения, соответствующая производной ∂₁/∂a  1:

 a   a .

Но ₀ — МНК-регрессия y по x в классе , а функция a  ₀(x) принадлежит этому же классу. Поэтому a  0, откуда следует доказываемое утверждение  .

Доказательство имеют много общего с рассмотренным в § 5 свойством регрессий, содержащих свободный член в качестве параметра; доказываемое утверждение также напоминает равенство (5.4). Однако существует различие между этими утверждениями. Наличие в качестве параметра свободного члена — свойство представления функций данного класса, в то время как здесь рассматривается свойство самого класса функций. Для иллюстрации различия рассмотрим пример.

Допустим, что некоторое устройство круглосуточно присоединено к электросети и в каждый момент находится в одном из двух режимов: ожидания или полезной работы. Ежесуточно фиксируются затраты электроэнергии (y) и суммарные (за сутки) продолжительности ожидания (u) и работы (v). Характерные часовые затраты энергии в каждом из режимов (b_u и b_v) оцениваются как параметры регрессии

Здесь функция регрессии не содержит свободного члена. Однако факторы u и v определены таким образом, что в любом наблюдении u  v  24, а поэтому прибавление к любой функции этого класса произвольной константы a равносильно прибавлению a/24 к каждому из параметров b_u и b_v. Поскольку на параметры не наложено никаких ограничений, новая функция принадлежит к исходному регрессионному классу, и поэтому найденные посредством МНК параметры удовлетворяют равенству

В отличие от этого регрессия вида , также не имеющая свободного члена, обсуждаемым здесь свойством не обладает: все функции вида (x)  bx удовлетворяют условию (0)  0, и прибавление ненулевой константы создаст функцию, не содержащуюся в исходном классе. Равенство при этом возможно лишь при специально подобранных данных.