§ 7. Ковариация и коэффициент корреляции

Выше, в §§ 4 и 5, были введены показатели тесноты статистической связи — дисперсионное и корреляционное отношения. Основой этих показателей является сопоставление полной вариации результативного признака и ее составляющих — объясненной и остаточной дисперсий. Такой подход к измерению тесноты статистической связи не является единственно возможным.

Другие показатели основаны на сопоставлении отклонений обоих взаимосвязанных признаков от их средних значений.

Рассмотрим корреляционное поле, приведенное на рис. 7.1а. Видно, что с возрастанием признака x признак y также преимущественно возрастает. Если бы связь была линейной функциональной, то для всех элементов, для которых , выполнялось бы неравенство , а для тех точек, у которых , было бы также . Графически бы это означало, что точки, расположенные правее прямой , располагались бы выше прямой , а точки, расположенные левее прямой , лежали бы ниже этой прямой. Все точки расположились бы в I и III квадрантах, а II и IV квадранты были бы пусты. Но изображенная на рисунке связь не функциональна, и некоторая часть точек лежит во II и IV квадрантах, хотя таких точек сравнительно немного.

Обратимся к корреляционному полю на рис. 7.1б. Здесь связь носит обратный характер: с возрастанием x признак y преимущественно убывает. Поэтому здесь заполнены главным образом II и IV квадранты, а квадранты I и III почти пусты.

Рис. 7.1

Третий случай представлен на рис. 7.1в. Здесь мы не отмечаем никакой связи между переменными, и все четыре квадранта заполнены примерно одинаково.

Введем обозначения для индивидуальных значений отклонений:

.

В квадрантах I и III знаки отклонений совпадают; в квадрантах II и IV знаки противоположны. Простейший показатель тесноты связи основан на подсчете элементов с совпадающими и противоположными знаками отклонений. Если больше элементов с совпадающими знаками, то связь прямая; если больше элементов с противоположными знаками — обратная. Количественно связь оценивается так называемым коэффициентом Фехнера:

где

– число элементов с совпадающими знаками отклонений;

– число элементов с противоположными знаками отклонений.

Этот показатель положителен для прямой зависимости между x и y (рис. 7.1а) и отрицателен для обратной зависимости (рис. 7.1б). При независимости признаков (рис. рис. 7.1в) . Его значения заключены в пределах:

.

При функциональной линейной связи .

Коэффициент Фехнера практически используется весьма редко. Его недостаток состоит в том, что он отражает только знаки отклонений и не учитывает их абсолютную величину. Значительно удобнее как характеристика связи между количественными признаками так называемая ковариация, определяемая как среднее произведение отклонений признаков x и y от собственных средних значений:

(7.1)

где N — объем совокупности. Так как при совпадении знаков отклонений произведение положительно, а при несовпадении — отрицательно, то в случае рис. 7.1а , а в случае рис. 7.1б . Для независимых признаков (рис. 7.1в) . Обратное утверждение в общем случае неверно: на рис. 7.2 представлено корреляционное поле, соответствующее сильной нелинейной связи. Если в силу симметрии для любой точки с отклонениями () найдется симметричная ей точка с отклонениями (), то окажется, что , хотя признаки заметно связаны.

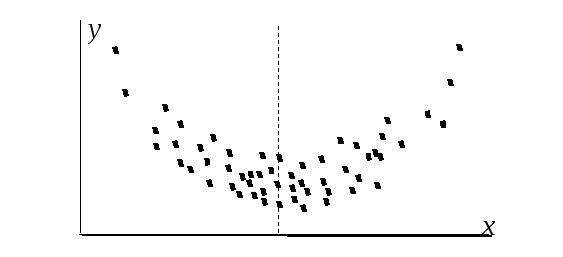
Рис. 7.2

Ковариация характеризует совместное изменение обоих признаков. Его размерность равна произведению размерностей признаков.

Ковариация может быть весьма полезна при решении задач, в которых характеристики распределения отдельных признаков недостаточны и необходимы характеристики взаимосвязи между признаками. Типичными являются следующие задачи.

Дисперсия суммы (разности). Пусть некоторая величина представляет собой сумму двух других величин:

.

В силу одного из свойств среднего арифметического

.

Определим дисперсию величины z:

то есть

(7.2)

Аналогично может быть получено выражение:

Пример. Исследуется множество технических разработок. Имеются данные о затратах на этапе теоретических исследований (x) и на этапе испытаний опытного образца (y):

Известно, что эти затраты взаимосвязаны: чем больше объем теоретических исследований, тем меньшие затраты приходится производить при испытаниях образцов:

(млн. руб.)²

Требуется определить среднее значение и среднее квадратическое отклонение суммарных затрат по обеим статьям.

Для среднего значения имеем:

При оценке вариации воспользуемся равенством (7.2):

(млн. руб.)².

Отсюда:

Среднее значение произведения. Преобразуем выражение для ковариации:

или

(7.3)

Отсюда следует выражение для среднего значения произведения:

(7.4)

Если величины независимы, то, как следует из выражения (7.4), ; если между x и y существует прямая зависимость, то , если же обратная зависимость, то .

Пример. Исследуется множество партий деталей. По данным о размерах партии x и затратах времени на обработку одной детали каждой партии y получены результаты:

Кроме того, известно, что в больших партиях на каждую деталь тратится меньше времени, чем в малых:

Требуется определить средние затраты времени () на обработку партии деталей.

Для каждой партии деталей время на обработку всей партии равно произведению объема партии на затраты времени на деталь:

Следовательно, средние затраты времени на партию деталей равны:

Ковариация является важной характеристикой зависимости, но, тем не менее, она не может выполнять функции показателя тесноты взаимосвязи. Как указывалось, она имеет размерность, следовательно, его величина зависит от выбора единицы измерения каждого из признаков. Кроме того, величина коэффициента ковариации, очевидно, тем больше, чем больше вариация каждого из признаков. Можно доказать¹, что справедливо неравенство

(7.5)

причем равенство имеет место тогда и только тогда, когда отклонения величин x и y пропорциональны:

где k — постоянное для данной совокупности число. Иными словами, если признаки x и y связаны функциональной линейной зависимостью, то .

От указанных недостатков ковариации свободен коэффициент корреляции, введенный в конце XIX века К. Пирсоном и Ф. Гальтоном:

или, в более подробной записи:

(7.6)

Коэффициент корреляции представляет собой отношение среднего значения произведения отклонений признаков к произведению их средних квадратических отклонений.

Коэффициент корреляции играет особо важную роль при изучении статистической взаимосвязи, поэтому остановимся подробнее на его свойствах.

1) Из свойства коэффициента ковариации вытекает, что коэффициент корреляции ограничен по абсолютной величине:

При этом равенство имеет место тогда и только тогда, когда рассматриваемые признаки связаны функциональной линейной зависимостью.

Если признаки независимы, то . Но коэффициент корреляции чувствителен не ко всякой связи, так что при некоторых видах нелинейной связи он также может равняться нулю. Если , говорят, что признаки линейно не коррелированны; в частном случае они могут быть независимы.

2) Так как коэффициент корреляции вычисляется только по отклонениям признаков, его величина не изменится при изменении начала отсчета одного или обоих признаков:

.

3) Если все значения признака умножить на одно и то же число, то все отклонения окажутся умноженными на это число: d_ax = a·d_x. То же произойдет и со средним квадратическим отклонением, если этот множитель положителен; в любом случае _ax = = |a|·_x. Таким образом, у числителя и у знаменателя в выражении (7.6) появятся множители, которые могут различаться только знаками, и абсолютная величина коэффициента корреляции останется без изменения. Она не изменится и в том случае, если такому преобразованию подвергнуть оба признака:

.

Отсюда, в частности, следует, что коэффициент корреляции не зависит от выбора единиц измерения признаков.

4) Свойства 2) и 3) могут быть объединены следующим свойством. Если

то

Знаки коэффициентов корреляции совпадут, если множители b и d имеют одинаковые знаки; в противном случае их знаки будут противоположны. Отсюда следует, что коэффициент корреляции не изменится при одновременном изменении начала отсчета и масштаба одного или обоих признаков (при этом b и d положительны).

Пример. Допустим, что из американского литературного источника мы узнаем, что коэффициент корреляции между расходом газа на отопление (y) и температурой наружного воздуха (x) равен – 0.99 (сильная убывающая зависимость). При этом температура измерялась в градусах Фаренгейта, а расход газа — в кубических футах. Если перейти к градусам Цельсия () и кубическим метрам (), то коэффициент корреляции при таком преобразовании признаков останется без изменения: – 0.99.

Вычисление коэффициента корреляции производится обычно путем определения ковариации с последующим делением результата на произведение . При этом, если данные не сгруппированы, ковариация вычисляется как простое среднее арифметическое из произведений отклонений признаков. Проиллюстрируем сказанное примером, использующим данные предыдущего параграфа о связи времени обработки деталей с величиной обрабатываемой поверхности. Расчеты сведены в таблицу 7.1.

Таблица 7.1. Пример расчета коэффициента корреляции

Номер детали	Обрабатываемая поверхность (x, см2)	Время обработки (y), мин.			(x –)2	(y –)2	(x –) (y –
1	100	3.0	– 150	– 2,0	22500	4.00	300
2	150	4.0	– 100	– 1,0	10000	1.00	100
3	150	4.5	– 100	– 0,5	10000	0.25	50
4	200	4.0	– 50	– 1,0	2500	1.00	50
5	250	5.0	0	0,0	0	0.00	0
6	250	4.5	0	– 0,5	0	0.25	0
7	250	6.0	0	1,0	0	1.00	0
8	300	5.5	50	0,5	2500	0.25	25
9	400	7.0	150	2,0	22500	4.00	300
10	450	6.5	200	1,0	40000	2.25	300
Сумма	2500	50.0	–	–	110000	14.00	1125
Среднее	250	5.0	–	–	11000	1.40	112.5

По средним квадратам отклонений — дисперсиям — находим средние квадратические отклонения:

Среднее значение в последнем столбце есть коэффициент ковариации: Отсюда коэффициент корреляции равен: