§ 4. Дисперсионное и корреляционное отношения

Метод анализа взаимосвязи, основанный на вычислении групповых средних, позволяет решить вопрос о наличии зависимости и о ее характере, форме. При этом остается открытым вопрос о тесноте взаимосвязи между факторами. Так, на рис.4.1 приведены корреляционное поле и построенная на нем эмпирическая линия регрессии; эта линия регрессии в точности совпадает с линией регрессии на рис. 3.1, но связь в этом случае (рис. 4.1), очевидно, значительно слабее. Большое рассеяние фактических точек относительно групповых средних свидетельствует о сильном влиянии посторонних причин на результат и, следовательно, об относительно более слабой связи последнего с выделенным признаком-фактором.

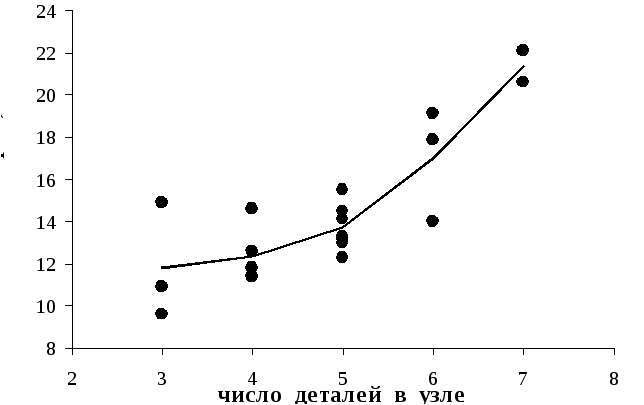
Рис. 4.1

Таким образом, в основу измерения тесноты взаимосвязи кладется измерение вариации результирующего признака и ее составляющих. При этом используется свойство разложимости дисперсии¹, описываемое следующим равенством²:

(4.1)

Здесь — полная дисперсия признака

(4.2)

т.е. средний квадрат отклонений фактических значений признака от среднего арифметического по всей совокупности. Величина представляет собой межгрупповую дисперсию

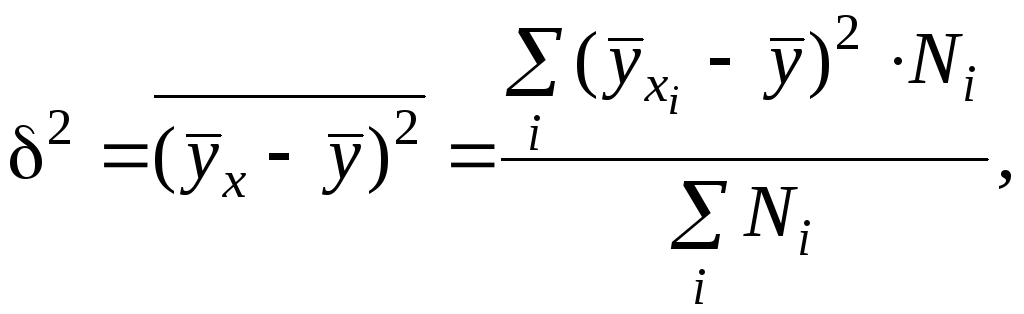(4.3)

или средний квадрат отклонений групповых средних от среднего по всей совокупности (при усреднении квадраты отклонений взвешиваются по численности отдельных групп N_i). Величина есть внутригрупповая дисперсия³

 ,

которая может быть вычислена путем усреднения дисперсий признака в отдельных группах с весами, равными численности групп:

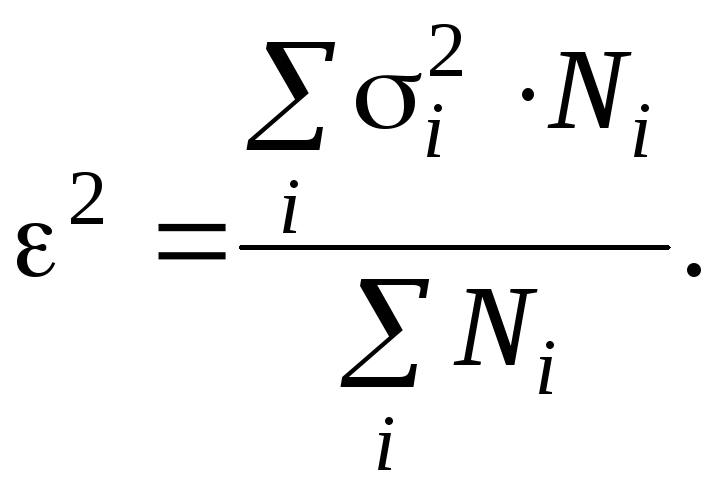(4.4)

Дисперсия признака в i-й группе есть средний квадрат отклонений его индивидуальных значений в i-й группе от группового среднего:

Суммирование в числителе производится по элементам i-й группы. Подставляя это выражение в (4.4), получим следующее выражение для внутригрупповой дисперсии:

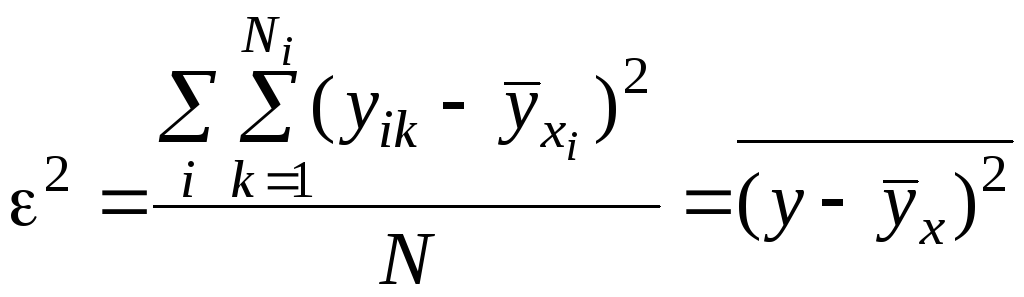
(4.5)

Здесь суммирование выполняется по всей совокупности, так как суммы по отдельным группам объединяются в общую сумму. Таким образом, внутригрупповой дисперсии можно дать также следующую интерпретацию: внутригрупповая дисперсия есть усредненный по всей совокупности квадрат отклонений индивидуальных значений признака от соответствующих групповых средних (т.е. рассматриваются отклонения значений признака для каждого элемента от среднего значения в своей группе).

При анализе зависимости результативного признака от некоторого фактора составляющие дисперсии играют различную роль. Межгрупповая дисперсия отражает различия между групповыми средними. Так как набор групповых средних характеризует зависимость результирующего признака от фактора, то межгрупповая дисперсия характеризует ту составляющую вариации результирующего признака, которая объясняется влиянием рассматриваемого фактора. Внутригрупповая дисперсия отражает вариацию результативного признака внутри групп, в которых признак-фактор имеет постоянное значение. Следовательно, эта составляющая дисперсии отражает влияние неучтенных причин. В анализе статистической связи используются специальные термины для обозначения составляющих дисперсии результативного признака: межгрупповая дисперсия носит название объясненной, внутригрупповая — остаточной.

При анализе взаимосвязи могут представляться следующие случаи:

1) связь функциональна. Так как при этом каждому значению фактора соответствует единственное значение результирующего признака, вариация внутри групп отсутствует и все индивидуальные значения совпадают со средними в своих группах. Остаточная дисперсия при этом равна нулю. Выражения (4.2) и (4.3) совпадают, и объясненная дисперсия совпадает с полной дисперсией результативного признака:

2) Признаки независимы. При этом распределения по признаку y всех групп одинаковы, следовательно, все групповые средние совпадают между собой и со средним по всей совокупности. В этом случае объясненная дисперсия равна нулю; равенство (4.2) теперь совпадает с (4.5), так как остаточная дисперсия равна полной:

3) Признаки взаимосвязаны, но связь носит корреляционный характер. Обе составляющие дисперсии при этом отличаются от нуля и в сумме дают полную дисперсию.

При этом чем теснее связь, тем большую долю полной дисперсии составляет объясненная дисперсия и тем меньшую часть составляет остаточная дисперсия.

Естественно использовать структуру дисперсии для измерения тесноты связи. Таким показателем является доля объясненной дисперсии в полной дисперсии результативного признака; эта величина носит название дисперсионного отношения (эмпирического коэффициента детерминации):

Средние квадратические отклонения дают более наглядное представление о вариации, чем дисперсии. Поэтому в качестве показателя тесноты связи используется также отношение объясненного среднего квадратического отклонения к полному:

Оно носит название эмпирического корреляционного отношения¹.

Дисперсионное и корреляционное отношения — безразмерные величины; их значения заключены в интервале от нуля до единицы:

0 ≤ ² ≤ 1; 0 ≤  ≤ 1.

Чем теснее связь между признаками, тем большее значение принимает корреляционное отношение. Оно равно единице тогда и только тогда, когда связь функциональна. Если результативный признак не зависит от фактора, корреляционное отношение равно нулю. Обратное утверждение, строго говоря, может не выполняться. Разбирая выше второй случай (независимость признаков), мы отметили, что в силу совпадения распределений отдельных групп групповые средние значения должны совпасть, поэтому объясненная дисперсия (а значит, и корреляционное отношение) равна нулю. Но равенство групповых средних еще не означает, что распределения групп совпадают; одни и те же средние значения могут получиться и при различных распределениях. Пример зависимости такого рода иллюстрируется корреляционным полем на рис. 4.2. Так как распределения групп различны, признаки в силу общего определения следует считать взаимосвязанными; однако эта связь не проявляется в виде различия групповых средних, и корреляционное отношение в этом случае равно нулю. Следует заметить, что такого рода зависимости сравнительно редки; кроме того, если зависимость не проявляется в виде различия средних значений, то такая взаимосвязь во многих отношениях несущественна. Поэтому корреляционное отношение является достаточно удобным показателем тесноты связи, хотя этот показатель чувствителен не ко всяким видам зависимости.

Рис. 4.2

Рис. 4.2

Рассмотрим пример вычисления корреляционного отношения. Для этого воспользуемся данными из предыдущего параграфа. Для количественной оценки тесноты связи необходимо кроме групповых средних располагать также значениями групповых дисперсий или средних квадратических отклонений. Результаты, полученные по данным таблицы 3.2, сведены в таблицу 4.1.

Таблица 4.1. К расчету корреляционного отношения

Число деталей в узле	Число узлов	Средняя по группе длительность сборки (), мин.	Дисперсия по группе (), мин.2
3	3	11.80	5.0867
4	5	12.36	1.4464
5	7	13.70	0.9857
6	3	17.00	4.7400
7	2	21.35	0.5625

Прежде всего, вычислим общее по всей совокупности узлов среднее значение длительности сборки:

Остаточная дисперсия может быть получена усреднением дисперсий отдельных групп:

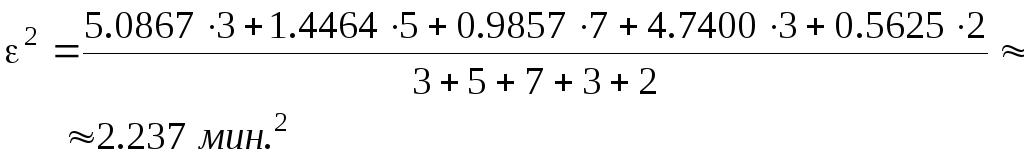
Остаточное среднее квадратическое отклонение равно

Усредняя квадраты отклонений групповых средних от общего, определим межгрупповую дисперсию:

Объясненное среднее квадратическое отклонение равно

Полная дисперсия может быть вычислена либо непосредственно по исходным данным, либо же, что в рассматриваемом случае проще, как сумма объясненной и остаточной дисперсий:

полное среднее квадратическое отклонение равно

Отсюда корреляционное отношение равно

Значение корреляционного отношения, близкое к единице, свидетельствует о довольно тесной связи между длительностью сборки узла и его сложностью.

При практическом использовании результатов анализа часто вместо фактических неизвестных значений результативного признака используются регрессионные (средние групповые) значения. Это вызывает ошибки, отклонения фактических результатов от расчетных. Среднее квадратическое отклонение такой ошибки совпадает с остаточным средним квадратическим отклонением результативного признака. Поэтому для нас представляет значительный практический интерес зависимость остаточной вариации от показателя тесноты связи.

Так как

то

откуда

(4.6)

Допустим, что нам предстоит решить задачу нормирования длительности сборки узлов. Не анализируя зависимости длительности сборки ни от каких факторов, мы могли бы в качестве нормативного времени сборки использовать среднее арифметическое по всей совокупности ; индивидуальные значения отклонялись бы от него в среднем квадратическом на величину Используя полученную зависимость от сложности узлов, мы можем установить дифференцированные нормы для узлов различной сложности в соответствии с регрессионными значениями. При этом также будут возникать отклонения индивидуальных значений от нормативных, но эти отклонения будут меньше, чем в первом случае: их среднее квадратическое значение равно остаточному среднему квадратическому отклонению. Уменьшение ошибки определяется множителем и в нашем случае равно

(эта величина у нас была раньше определена непосредственно по данным о вариации в отдельных группах; расхождение в последнем знаке связано с погрешностями округления при вычислениях).

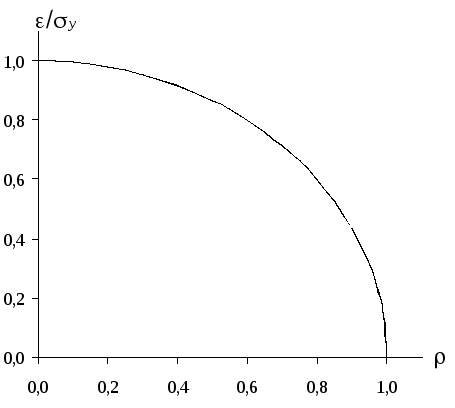
Рис. 4.3

Рис. 4. 3

Уменьшение остаточной вариации с ростом корреляционного отношения представлено на графике (рис. 4.3). В соответствии с равенством (4.6) он представляет собой дугу окружности. Из графика видно, что небольшие значения  практически не уменьшают остаточного среднего квадратического отклонения, и лишь достаточно близкие к единице значения корреляционного отношения дают существенный эффект с точки зрения уменьшения остаточной вариации.